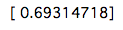J'ai essayé d'implémenter la régression logistique de Cousera en Python

Cousera - J'ai mis en œuvre la régression logistique de la semaine d'apprentissage automatique du Dr Andrew Ng3. J'ai essayé d'utiliser uniquement numpy autant que possible.

La magie coutumière.

%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt

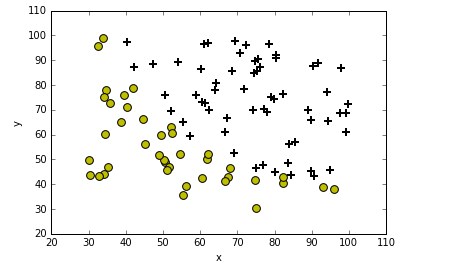
Lisez les données et tracez-les.

def plotData(data):
    neg = data[:,2] == 0
    pos = data[:,2] == 1

    plt.scatter(data[pos][:,0], data[pos][:,1], marker='+', c='k', s=60, linewidth=2)
    plt.scatter(data[neg][:,0], data[neg][:,1], c='y', s=60)
    plt.xlabel('x')
    plt.ylabel('y')
    plt.legend(frameon= True, fancybox = True)
    plt.show()


data = np.loadtxt('ex2data1.txt', delimiter=',')
plotData(data)

Ensuite, implémentation de la fonction de coût et de la fonction sigmoïde

Fonction Sigmaid

Fonction de coût

def sigmoid(z):
    return(1 / (1 + np.exp(-z)))

def CostFunction(theta, X, y):
    m = len(y)
    h = sigmoid(X.dot(theta))
    
    j = -1*(1/m)*(np.log(h).T.dot(y)+np.log(1-h).T.dot(1-y))
    
    return j
    
    

Regardons le premier coût.

X = np.c_[np.ones((data.shape[0],1)), data[:,0:2]]
y = np.c_[data[:,2]]

initial_theta = np.zeros(X.shape[1])
cost = CostFunction(initial_theta, X, y)
print(cost)

Le coût est comme ça. Vient ensuite la mise en œuvre de la méthode de descente la plus raide.

def gradient_decent (theta, X, y, alpha = 0.001, num_iters = 100000):
    m = len(y)
    history = np.zeros(num_iters)
    
    for inter in np.arange(num_iters):
        h = sigmoid(X.dot(theta))
        theta = theta - alpha *(1/m)*(X.T.dot(h-y))
        history[inter] = CostFunction(theta,X,y)

    return(theta, history)
    
initial_theta = np.zeros(X.shape[1])
theta = initial_theta.reshape(-1,1)
cost = CostFunction(initial_theta,X,y)
theta, Cost_h= gradient_decent(theta, X, y)

print(theta)
plt.plot(Cost_h)
plt.ylabel('Cost_h')
plt.xlabel('interation')
plt.show()

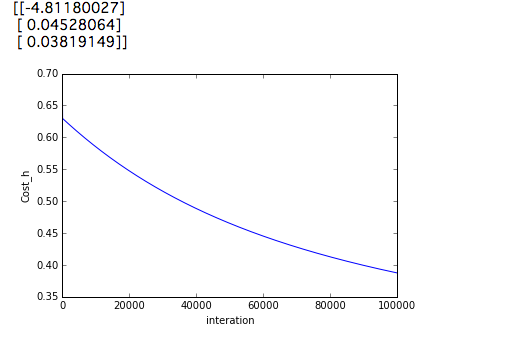
Le résultat de son exécution est le suivant.

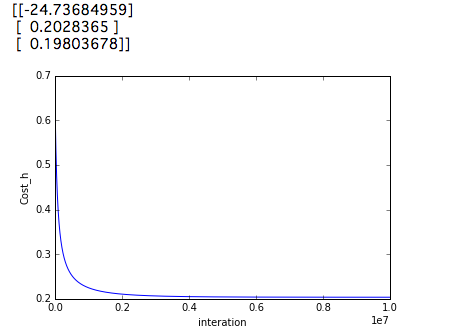
Pour une raison quelconque, cela donne de meilleurs résultats que de définir num_iters sur 10000000. Voyons le résultat.

def predict(theta, X, threshold = 0.5):
    p = sigmoid(X.dot(theta)) >= threshold
    
    return(p.astype('int'))

p = predict(theta,X)
y = y.astype('int')

accuracy_cnt = 0
for i in range(len(y)):
    if p[i,0] == y[i,0]:
        accuracy_cnt +=1

print(accuracy_cnt/len(y) * 100)
    

L'exécution du code ci-dessus vous donnera 91,0%. Et si vous exécutez num_inter à 1000000? ..

Si vous vérifiez cette précision, elle sera de 89,0%. On ne sait pas pourquoi les résultats ci-dessus sont pires, malgré les coûts inférieurs.

référence

https://github.com/JWarmenhoven/Coursera-Machine-Learning