Implémentation des règles d'apprentissage Perceptron en Python

À propos de cet article

J'ai implémenté la règle d'apprentissage de Perceptron, qui est l'une des méthodes pour déterminer la limite de discrimination pour les groupes de données linéairement séparables, en Python sans utiliser de bibliothèque. Étant donné que je suis un débutant en Python et en apprentissage automatique, veuillez signaler les mauvais points.

Pour "Widrow-Hoff Learning Rules", qui est comparé aux "Perceptron Learning Rules", ["Implementing Widrow-Hoff Learning Rules in Python"](http: / /qiita.com/s-kiriki/items/6a90beede4c139558bcc).

Théorie des règles d'apprentissage de Perceptron

Le plan et les formules des règles d'apprentissage de Perceptron sont résumés grossièrement dans la diapositive ci-dessous (à partir du milieu de la diapositive).

https://speakerdeck.com/kirikisinya/xin-zhe-renaiprmlmian-qiang-hui-at-ban-zang-men-number-2

la mise en oeuvre

Pour une dimension

Trouvez la limite de séparation des données d'apprentissage séparables linéairement qui existent sur une dimension, comme illustré dans la figure ci-dessous et qui appartiennent à l'une des deux classes.

Comme point de mise en œuvre,

• Le vecteur de poids initial est «w = (0,2,0,3)» et le coefficient d'apprentissage est «ρ = 0,5».
• Nous n'avons pas jugé la convergence de la frontière de séparation, et avons répété la correction (apprentissage) du vecteur de poids un nombre suffisant de fois (100 fois) (je pense que ce n'est pas vraiment bien, mais j'ai pensé qu'il serait bon de laisser la machine faire beaucoup de travail. .)

Le code réel ressemble à ceci:

# coding: UTF-8
#Exemple d'implémentation d'une règle d'apprentissage Perceptron unidimensionnelle
import numpy as np
import matplotlib.pyplot as plt

def train(wvec, xvec, is_c1):
    low = 0.5#Coefficient d'apprentissage
    if (np.dot(wvec,xvec) > 0) != is_c1:
        if is_c1:
            wvec_new = wvec + low*xvec
        else:
            wvec_new = wvec - low*xvec
        return wvec_new
    else:
        return wvec

if __name__ == '__main__':
    
    data = np.array([[1.0, 1],[0.5, 1],[-0.2, 2],[-1.3, 2]])#Groupe de données
    
    features = data[:,0].reshape(data[:,0].size,1)#Vecteur caractéristique
    labels = data[:,1]#Classe (cette fois c1=1,c2=2）
    wvec = np.array([0.2, 0.3])#Vecteur de poids initial
    is_c1s = (labels == 1)#Un tableau de c1 ou booléen
    
    xvecs = np.c_[np.ones(features.size), features]#xvec[0] = 1
    
    loop = 100
    for j in range(loop):
        for xvec, is_c1 in zip(xvecs, is_c1s):
            wvec = train(wvec, xvec, is_c1)
    
    print wvec
    print -(wvec[0]/wvec[1])
    
    #Représentation graphique
    plt.axhline(y=0, c='gray')
    plt.scatter(features[is_c1s], np.zeros(features[is_c1s].size), c='red', marker="o")
    plt.scatter(features[~is_c1s], np.zeros(features[~is_c1s].size), c='yellow', marker="o")
    #Frontière de séparation
    plt.axvline(x=-(wvec[0]/wvec[1]), c='green')    
    plt.show()

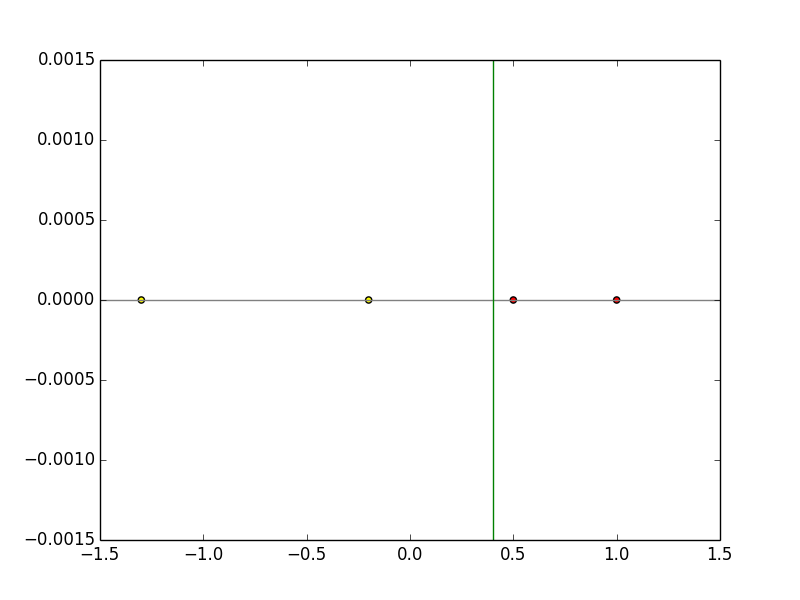
Le vecteur de poids après l'entraînement est «w = (-0,3, 0,75)». En remplaçant cela par la formule «wx = 0», la fonction discriminante devient «x = 0,4», et on peut voir que la séparation linéaire est effectuée avec succès par apprentissage comme le montre la figure ci-dessous.

Dans le cas de 2 dimensions

Comme le montre la figure ci-dessous (image), recherchez la ligne de séparation des données d'apprentissage séparables linéairement qui existe en deux dimensions et appartient à l'une des deux classes.

Comme point de mise en œuvre,

• Utilisez np.random.rand pour générer deux classes de données linéairement séparables
• Le vecteur de poids initial est «w = (2, -1,3)» et le coefficient d'apprentissage est «ρ = 0,5».
• Comme dans le cas d'une dimension, le jugement de convergence de la frontière de séparation n'a pas été effectué et la correction (apprentissage) du vecteur de poids a été répétée un nombre suffisant de fois (100 fois).

Le code réel ressemble à ceci:

# coding: UTF-8
#Exemple d'implémentation de la règle d'apprentissage 2D Perceptron
import numpy as np
import matplotlib.pyplot as plt
import sys

def train(wvec, xvec, label):
    low = 0.5#Coefficient d'apprentissage
    if (np.dot(wvec,xvec) * label < 0):
        wvec_new = wvec + label*low*xvec
        return wvec_new
    else:
        return wvec

if __name__ == '__main__':
    
    train_num = 100#Nombre de données d'entraînement
    
    #Données d'entraînement de classe 1
    x1_1=np.random.rand(train_num/2) * 5 + 1 #x composant
    x1_2=np.random.rand(int(train_num/2)) * 5 + 1 #composant y
    label_x1 = np.ones(train_num/2) #Étiquette (tous 1)
    
    #Données d'entraînement de classe 2
    x2_1=(np.random.rand(train_num/2) * 5 + 1) * -1 #x composant
    x2_2=(np.random.rand(train_num/2) * 5 + 1) * -1 #composant y
    label_x2 = np.ones(train_num/2) * -1 #Libellés (tous-1）
    
    x0=np.ones(train_num/2) #x0 est toujours 1
    x1=np.c_[x0, x1_1, x1_2]
    x2=np.c_[x0, x2_1, x2_2]
    
    xvecs=np.r_[x1, x2]
    labels = np.r_[label_x1, label_x2]
    
    wvec = np.array([2,-1,3])#Vecteur de poids initial Déterminer de manière appropriée
    
    loop = 100
    for j in range(loop):
        for xvec, label in zip(xvecs, labels):
            wvec = train(wvec, xvec, label)
    
    print wvec
    
    plt.scatter(x1[:,1], x1[:,2], c='red', marker="o")
    plt.scatter(x2[:,1], x2[:,2], c='yellow', marker="o")
    #Frontière de séparation
    x_fig = np.array(range(-8,8))
    y_fig = -(wvec[1]/wvec[2])*x_fig - (wvec[0]/wvec[2])
    
    plt.plot(x_fig,y_fig)
    plt.show()

Puisque les données d'entraînement sont générées de manière aléatoire, le vecteur de poids et la fonction discriminante après l'entraînement sont différents à chaque fois, À titre d'exemple du résultat d'exécution réel, il est montré dans la figure ci-dessous, et on peut voir que la séparation linéaire est effectuée avec succès par apprentissage.