Python: Diagramme de distribution de données bidimensionnelle (estimation de la densité du noyau)
introduction
Je voulais voir l'état de distribution des données distribuées en deux dimensions, j'ai donc essayé d'estimer la densité du noyau avec scipy.stats.gaussian_kde```. Le diagramme de résultat est le suivant. ( bw_method = 'scott' '``)

À propos, l'analyse de régression simple est effectuée en douceur avec `` numpy '' comme suit. (Lorsque vous faites diverses choses, il est important que ce code sorte immédiatement et puisse être utilisé, alors j'ose l'écrire.)
def sreq(x,y):
# y=a*x+b
res=np.polyfit(x, y, 1)
a=res[0]
b=res[1]
coef = np.corrcoef(x, y)
r=coef[0,1]
return a,b,r
Comment faire
La méthode était la suivante. Merci, affiche.
L'ingéniosité est la suivante.
Comme l'affichage + est plus simple sur l'axe logarithmique, j'ai choisi l'axe logarithmique, mais je voulais aussi lire les valeurs numériques sur l'axe, j'ai donc dessiné l'axe logarithmique manuellement. Le traitement des données est effectué en prenant le logarithme commun des données brutes.
- J'ai contrôlé l'intervalle de dessin des courbes de niveau par moi-même. Puisque la densité de probabilité peut être obtenue avec
[0,01, 0,1, 0,3, 0,5, 0,7, 0,9, 1,0]. Il y a. La valeur minimale de 0,01 dans la liste a été définie visuellement pour couvrir la plage des données. La valeur maximale de 1,0 est ajoutée car sans elle, la plage de 0,9 ou plus ne sera pas colorée et sera délimitée. Notez que ** cette valeur n'indique pas de valeur de probabilité **. C'est juste pour ajuster l'apparence.
Essayez de changer les paramètres. .. ..
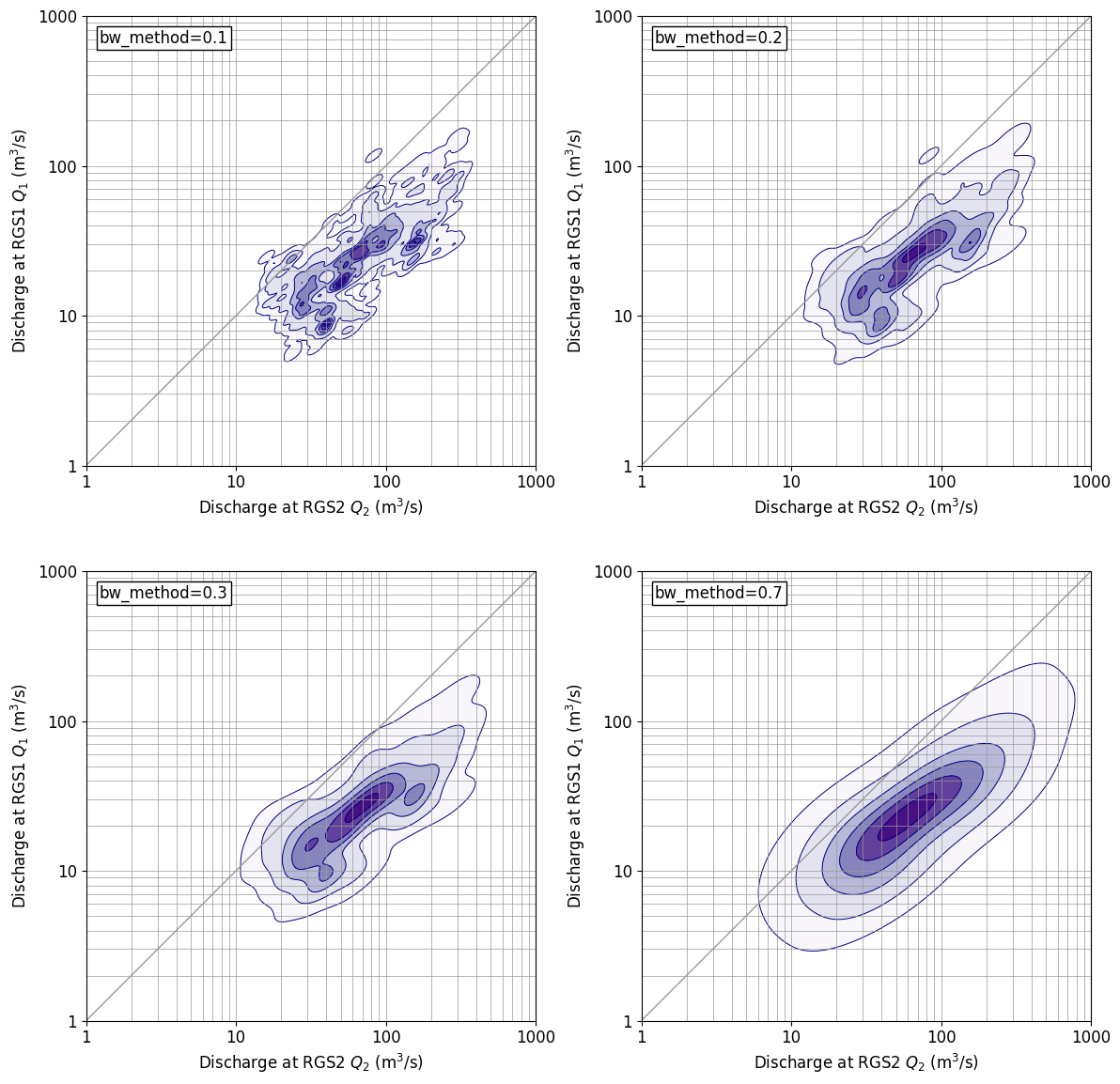
gaussin_bw pour kde_Il existe un paramètre appelé méthode, et si vous le modifiez, vous pouvez modifier la finesse de l'affichage de la forme de distribution. Le diagramme de résultat ci-dessus est la valeur par défaut, bw_method=Dans le cas de «scott», bw ci-dessous_Le chiffre lorsque la méthode est modifiée est affiché. pc_method=0.S'il est 3, la distribution est proche de la valeur par défaut. pc_Lorsque la valeur de la méthode augmente, l'affichage devient plus grossier et pb_method=0.S'il vaut 7, l'affichage est proche de la distribution normale normale bidimensionnelle.
## programme
Le programme qui a créé le diagramme de résultats présenté dans «Introduction» est illustré ci-dessous. Si vous voulez essayer ce programme, essayez de créer les données comme vous le souhaitez.
```python
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import matplotlib.cm as cm
from scipy.stats import gaussian_kde
def sreq(x,y):
# y=a*x+b
res=np.polyfit(x, y, 1)
a=res[0]
b=res[1]
coef = np.corrcoef(x, y)
r=coef[0,1]
return a,b,r
def inp_obs():
fnameR='df_rgs1_tank_inp.csv'
df1_obs=pd.read_csv(fnameR, header=0, index_col=0) # read excel data
df1_obs.index = pd.to_datetime(df1_obs.index, format='%Y/%m/%d')
df1_obs=df1_obs['2016/01/01':'2018/12/31']
#
fnameR='df_rgs2_tank_inp.csv'
df2_obs=pd.read_csv(fnameR, header=0, index_col=0) # read excel data
df2_obs.index = pd.to_datetime(df2_obs.index, format='%Y/%m/%d')
df2_obs=df2_obs['2016/01/01':'2018/12/31']
#
return df1_obs,df2_obs
def drawfig(x,y,sstr,fnameF):
fsz=12
xmin=0; xmax=3
ymin=0; ymax=3
plt.figure(figsize=(12,6),facecolor='w')
plt.rcParams['font.size']=fsz
plt.rcParams['font.family']='sans-serif'
#
for iii in [1,2]:
nplt=120+iii
plt.subplot(nplt)
plt.xlim([xmin,xmax])
plt.ylim([ymin,ymax])
plt.xlabel('Discharge at RGS2 $Q_2$ (m$^3$/s)')
plt.ylabel('Discharge at RGS1 $Q_1$ (m$^3$/s)')
plt.gca().set_aspect('equal',adjustable='box')
plt.xticks([0,1,2,3], [1,10,100,1000])
plt.yticks([0,1,2,3], [1,10,100,1000])
bb=np.array([1,2,3,4,5,6,7,8,9,10,20,30,40,50,60,70,80,90,100,200,300,400,500,600,700,800,900,1000])
bl=np.log10(bb)
for a0 in bl:
plt.plot([xmin,xmax],[a0,a0],'-',color='#999999',lw=0.5)
plt.plot([a0,a0],[ymin,ymax],'-',color='#999999',lw=0.5)
plt.plot([xmin,xmax],[ymin,ymax],'-',color='#999999',lw=1)
#
if iii==1:
plt.plot(x,y,'o',ms=2,color='#000080',markerfacecolor='#ffffff',markeredgewidth=0.5)
a,b,r=sreq(x,y)
x1=np.min(x)-0.1; y1=a*x1+b
x2=np.max(x)+0.1; y2=a*x2+b
plt.plot([x1,x2],[y1,y2],'-',color='#ff0000',lw=2)
tstr=sstr+'\n$\log(Q_1)=a * \log(Q_2) + b$'
tstr=tstr+'\na={0:.3f}, b={1:.3f} (r={2:.3f})'.format(a,b,r)
#
if iii==2:
tstr=sstr+'\n(kernel density estimation)'
xx,yy = np.mgrid[xmin:xmax:0.01,ymin:ymax:0.01]
positions = np.vstack([xx.ravel(),yy.ravel()])
value = np.vstack([x,y])
kernel = gaussian_kde(value, bw_method='scott')
#kernel = gaussian_kde(value, bw_method=0.1)
f = np.reshape(kernel(positions).T, xx.shape)
f=f/np.max(f)
ll=[0.01, 0.1, 0.3, 0.5, 0.7, 0.9, 1.0]
plt.contourf(xx,yy,f,cmap=cm.Purples,levels=ll)
plt.contour(xx,yy,f,colors='#000080',linewidths=0.7,levels=ll)
xs=xmin+0.03*(xmax-xmin)
ys=ymin+0.97*(ymax-ymin)
plt.text(xs, ys, tstr, ha='left', va='top', rotation=0, size=fsz,
bbox=dict(boxstyle='square,pad=0.2', fc='#ffffff', ec='#000000', lw=1))
#
plt.tight_layout()
plt.savefig(fnameF, dpi=100, bbox_inches="tight", pad_inches=0.1)
plt.show()
def main():
df1_obs, df2_obs =inp_obs()
fnameF='_fig_cor_test1.png'
sstr='Observed discharge (2016-2018)'
xx=df2_obs['Q'].values
yy=df1_obs['Q'].values
xx=np.log10(xx)
yy=np.log10(yy)
drawfig(xx,yy,sstr,fnameF)
#==============
# Execution
#==============
if __name__ == '__main__': main()
c'est tout
Recommended Posts