[Mathématiques] Si vous comprenez graphiquement la signification de «produit interne», vous pouvez voir différentes choses.

Quand on commence à étudier l'algèbre linéaire, ça sort assez vite, n'est-ce pas? Le calcul lui-même n'est pas si difficile, mais je pense qu'il y a des gens qui ne font pas les choses correctement. Moi aussi, j'étais comme ça. Donc, dans cette série de visualisation, je me concentrerai sur le "produit intérieur".

Aussi, dans les statistiques, il y a des choses qui peuvent être comprises par le produit intérieur partout, et il devient "produit intérieur": grin:. Les vecteurs sont une séquence de données, ils sont donc très pertinents pour les statistiques. Il sera traité dans les statistiques à partir de la prochaine fois, mais d'abord à partir du produit interne.

0. Une petite conclusion d'abord

Puisque la théorie précédente est nécessaire, je voudrais d'abord n'écrire que la conclusion de la signification du produit intérieur. Le produit interne peut être écrit comme une formule mathématique comme suit.

{\bf a}\cdot{\bf b} = \|{\bf a}\|\|{\bf b}\|\ \cos\theta

Pour l'exprimer visuellement, cela devient comme suit, et on peut lui donner la signification de la longueur du vecteur $ {\ bf a} $ multipliée par la longueur du vecteur $ {\ bf c} . Je vais. ( {\ bf c} $ est une projection du vecteur $ {\ bf b} $ sur le vecteur $ {\ bf a} $.)

Jusqu'à présent, si vous dites "Ouais, c'est vrai", attendez un moment car je vous expliquerai comment le produit interne est bien géré dans les statistiques la prochaine fois. (La version des diapositives ayant déjà été expliquée, veuillez consulter ** ici ** jusque-là)

Si vous voulez savoir "pourquoi vous pouvez dire ceci" et "ce que c'est", je voudrais l'expliquer à partir de maintenant, alors veuillez procéder tel quel.

1. Définition et calcul du produit intérieur

Commençons par la définition mathématique. Lorsqu'il y a un vecteur $ {\ bf a} = (a_1, \ cdots, a_n), {\ bf b} = (b_1, \ cdots, b_n) $, le produit interne est défini comme suit.

{\bf a} \cdot {\bf b} = a_1b_1+\cdots+a_nb_n = \sum_{i=1}^n a_ib_i

Cela signifie multiplier les éléments correspondants de chaque élément vectoriel (le premier élément $ a_1 $ et le premier élément $ b_1 $ correspondent etc ...) et les additionner tous ensemble. Considérons la signification visuelle de ceci.

2. Application du théorème cosinus

Pour comprendre le produit interne, nous utilisons le théorème du cosinus. La formule est ci-dessous.

\|{\bf b}-{\bf a}\|^2 = \|{\bf a}\|^2 + \|{\bf b}\|^2 - 2\|{\bf a}\|\|{\bf b}\|\ \cos\theta　　　　\cdots (*)

La relation entre les longueurs de chaque côté du triangle comme décrit ci-dessus satisfait cette relation de formule.

Aussi, le carré de la longueur de $ {\ bf a} $

\|{\bf a}\|^2 = \left(\sqrt{a_1\cdot a_1 + \cdots + a_n\cdot a_n}\right)^2 =a_1\cdot a_1 + \cdots + a_n\cdot a_n\\
=\sum_{i=1}^n x_i^2 = {\bf a} \cdot {\bf a}　

Peut être représenté par le produit interne du même vecteur. cette\||{\bf b}-{\bf a}\||^2Lorsqu'il est appliqué à

\|{\bf b}-{\bf a}\|^2 = ({\bf b}-{\bf a})\cdot({\bf b}-{\bf a}) = {\bf a}\cdot{\bf a} +  {\bf b}\cdot{\bf b} - 2 {\bf a}\cdot{\bf b} \\
= \|{\bf a}\|^2 + \|{\bf b}\|^2 - 2 {\bf a}\cdot{\bf b} 　　　　　　　　

En substituant cela à l'équation (*) du théorème du cosinus,

\|{\bf b}-{\bf a}\|^2 = \|{\bf a}\|^2 + \|{\bf b}\|^2 - 2\|{\bf a}\|\|{\bf b}\|\ cos\theta\\
\Rightarrow \|{\bf a}\|^2 + \|{\bf b}\|^2 - 2 {\bf a}\cdot{\bf b} = \|{\bf a}\|^2 + \|{\bf b}\|^2 - 2\|{\bf a}\|\|{\bf b}\|\ cos\theta\\

Sur les deux côtés\||\{\bf a}\||^2 + \||\{\bf b}\||\^2Parce qu'il y a, effacez-le,

 - 2 {\bf a}\cdot{\bf b} = - 2\|{\bf a}\|\|{\bf b}\|\ cos\theta \\
\Rightarrow {\bf a}\cdot{\bf b} = \|{\bf a}\|\|{\bf b}\|\ cos\theta

Ainsi, le produit intérieur est

\|{\bf a}\|\|{\bf b}\|\ \cos \theta

Il s'est avéré être.
Wow, je vois ...? ?? ??
Et alors? Je me sens··· Mais cette forme est très importante, alors souvenez-vous-en. Ensuite ceci\||{\bf a}\||\||{\bf b}\||\ \cos\thetaVoyons qui est.

3.||a|| ||b||Explorez le mystère de cosθ#

3.1 Reconfirmation du cos θ et du concept de projection

Tout d'abord, je voudrais reconfirmer $ \ cos \ theta $ une fois de plus. La définition mathématique est

\cos \theta = \frac{\|c\|}{\|r\|}

est. Montré dans le graphique

$ r $ est le rayon et $ x $ est le vecteur du vecteur $ r $ à ce point, dessinant une ligne perpendiculaire à l'axe des x. En tant qu'image, comme illustré ci-dessous, c'est la partie qui éclaire la lumière directement au-dessus et devient une ombre. (Cela s'appelle la projection.) ** La partie d'ombre créée en éclairant le toit $ {\ bf r} $ est le vecteur $ {\ bf c} $. ** **

3.2 Signification du produit intérieur

\cos \theta = \||c\||\ /\ ||r\||Des deux côtés de\||r\||Et le dénominateur\||r\||Vers la section opposée,

\|c\| = \|r\|\cos \theta

Donc la longueur de c est\||r\||\cos \thetaPeut être considéré comme.À la longueur du toit\cos \thetaOn pense qu'il a été multiplié par.

Au fait, voici les devoirs de la section précédente

\|{\bf a}\|\|{\bf b}\|\ \cos \theta

Revenons à. De même, essayez de faire briller une lumière d'en haut.

vecteur{\bf b}からvecteur{\bf a}上に射影してできたvecteurを{\bf c}Ensuite, si vous appliquez la logique ci-dessus, la longueur sera "à la longueur du toit.\cos \thetaParce que c'est un produit de\||{\bf b}\|| \cos \thetaSera. Vous avez maintenant tout le matériel dont vous avez besoin. Produit interne $ {\ bf a} \ cdot {\ bf b} $

{\bf a}\cdot{\bf b} = \|{\bf a}\|\|{\bf b}\|\ \cos\theta

Donc, ** "longueur du vecteur $ {\ bf a} $" ** et ** "longueur du vecteur $ {\ bf b} $ projetée sur le vecteur $ {\ bf a} $" Il est considéré comme le produit de **.

Puisque le produit intérieur est aussi ** "produit" **, c'est une sorte de multiplication, mais je pense que l'image de la ** multiplication entre vecteurs devrait être l'image de la correspondance des directions et de la multiplication de la longueur **. Je suis.

3.3 Lorsque les directions des deux vecteurs sont verticales

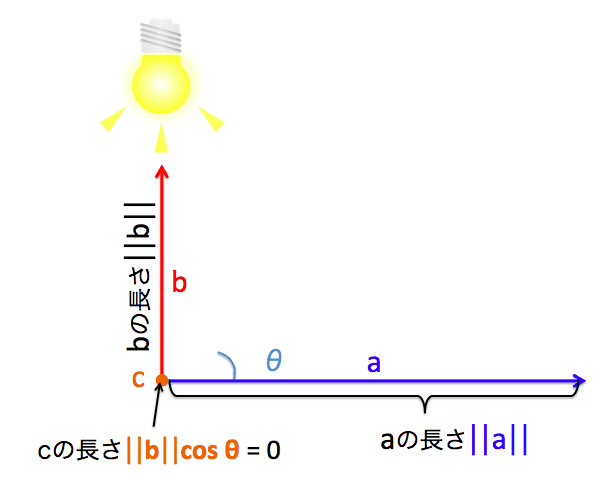
Si l'angle entre les deux vecteurs est correct, vous ne pouvez pas projeter une ombre même si vous projetez une lumière d'en haut. Par conséquent, à ce moment, la longueur du vecteur $ {\ bf c} $ devient 0. En d'autres termes, lorsque l'angle est correct, le produit intérieur est également 0.

3.3 Pour un vecteur de longueur 1

Facilitez l'histoire||r||=1, ||x||=1Supposons que c'était le cas.\cos \thetaLa définition de

\cos \theta = \frac{\|c\|}{\|r\|} = \|c\|

Par conséquent, la longueur de $ {\ bf c} $ devient la valeur de $ \ cos \ theta $ telle quelle.

Maintenant, si vous regardez le produit interne de $ {\ bf x} $ et $ {\ bf r} $,

{\bf x}\cdot{\bf r} = \|{\bf x}\|\|{\bf r}\|\ \cos\theta　=　1 \cdot 1 \cdot \cos\theta　=　\cos\theta 

Par conséquent, le produit interne de deux vecteurs de longueur 1 est $ \ cos \ theta $ **: smile:

Dans le prochain article, j'écrirai sur "des scènes où des produits internes sont utilisés dans les statistiques". J'expliquerai à quoi ressemblent la variance / écart type, le coefficient de covariance / corrélation, le coefficient de régression, etc. par rapport à ce produit interne à l'aide de graphiques et d'animations en Python.