J'ai lu "Quantum Computer Accelerates Artificial Intelligence" et j'ai essayé de le décrire en Python sans utiliser de formules mathématiques.
Cet article est l'article du 21/12 du Calendrier de l'Avent WACUL 2016.
Bonjour, le data sign en steam de WACUL, c'est @onhrs que le travail d'analyse de données.
Plus récemment, j'ai travaillé sur le traitement du langage naturel et d'autres analyses de données liées à l'apprentissage automatique.
Cette fois, le Dr Hidetoshi Nishimori et le Dr Masayuki Ozeki [Quantum Computer Accelerates Artificial Intelligence](https://www.amazon.co.jp/ Quantum Computer Accelerates Artificial Intelligence-Nishimori-Hidetoshi / dp / 4822251896 / ref = sr_1_1? Ie = UTF8 & qid = 1481941470 & sr = 8-1 & keywords = Nishimori% E3% 80% 80 Quantum), donc la situation réelle de ** intelligence artificielle x ordinateur quantique ** en ligne avec le contenu du livre Je veux parler de. (Nous visions les personnes qui ne comprennent pas la physique et les mathématiques à les comprendre.)
J'ai également essayé de donner un aperçu de l'utilisation de Python sans utiliser de formules. Même si je ne comprends pas les détails, j'ai essayé de les rendre visibles et compréhensibles.
Je suis motivé pour publier des articles autres que le calendrier de l'Avent, je vous serais donc reconnaissant si vous le souhaitez. (Lol)
Public cible de cet article
・ Ceux qui veulent en savoir plus sur les ordinateurs quantiques et le recuit quantique ・ Ceux qui veulent connaître l'état actuel et le potentiel futur des ordinateurs quantiques ・ Ceux qui veulent connaître la relation entre les ordinateurs quantiques et l'intelligence artificielle ・ Ceux qui veulent se lancer dans la science des données avec Python
Environnement attendu
Langue: Python3 Vous avez besoin de NumPy, SciPy, matplotlib, etc., mais vous pouvez ajouter Anaconda.
Editeur: Jupyter (bien sûr, les autres éditeurs vont bien)
En tant que mot-clé
Je pense qu'il y aura des mots ésotériques et des termes inconnus. Voici un résumé des mots importants, des mots clés et de leurs brefs aperçus pour la préparation et pour un examen ultérieur. (Ce n'est pas grave s'il y a des mots que vous ne comprenez pas à ce stade. Dans ce cas, ignorez-les.)
- La commande est appropriée.
- Ce n'est pas une définition stricte, mais plutôt, il y a des endroits où nous mentons parce que nous recherchons la clarté, mais veuillez la reconstruire après l'avoir comprise. (Rires) Afin d'avoir une bonne compréhension, il est essentiel de comprendre la ** mécanique statistique ** et la ** mécanique quantique **.
Apprentissage automatique
C'est difficile à expliquer aussi facilement que ces mots, mais le but est d'utiliser des méthodes statistiques pour trouver les modèles qui peuvent être obtenus à partir d'eux. C'est une méthode indispensable pour l'analyse actuelle du Big Data.
Apprentissage profond (ou apprentissage profond)
Une méthode pour effectuer un apprentissage automatique à l'aide d'une méthode qui imite le cerveau (réseau neuronal).
C'est très utile lorsque vous avez beaucoup de données, y compris le jugement d'image.
- À proprement parler, il ne doit pas nécessairement s'agir d'une structure multicouche, et l'apprentissage en profondeur ne doit pas nécessairement être une structure de réseau neuronal.
Ordinateur quantique
Contrairement aux ordinateurs conventionnels qui effectuent des calculs avec des nombres binaires de «0» et de «1», «** ondes **» générées dans le monde microscopique (extrêmement en expansion) des atomes et des molécules appelé mécanique quantique. Un ordinateur qui utilise les propriétés de.
Recuit quantique
Le problème d'optimisation, qui est une méthode qui prend beaucoup de temps pour calculer tous les chemins, est calculé à grande vitesse en utilisant le phénomène d'onde mentionné ci-dessus de la mécanique quantique. Aussi connue sous le nom de méthode de gravure quantique.
Bit quantique
Alors que les bits normaux ne peuvent représenter que «0» et «1», les bits quantiques sont des ondes, comme mentionné ci-dessus, ils peuvent donc être superposés. Vous pouvez exprimer l'ambiguïté d'être 1 et 0. (Les détails peuvent être compris en comprenant l'enchevêtrement quantique.)
Enchevêtrement quantique
C'est l'état quantique de la superposition ci-dessus elle-même. Puisqu'une substance est aussi une onde dans le monde quantique, elle se superpose, c'est donc l'état lui-même. (Peut-être que c'est la compréhension.)
- Pour le dire de manière difficile, lorsqu'on considère deux particules (ondes), c'est la corrélation qu'elles reçoivent l'une de l'autre. Si un état est déterminé, l'autre état est également déterminé. La téléportation quantique utilise ce phénomène.
Recuit simulé
Il est dérivé du phénomène de "cuisson", qui est un phénomène dans lequel la structure cristalline devient belle lorsque la température est lentement abaissée alors que le métal est à une température élevée. Cette méthode de minimisation de l'énergie cristalline est remplacée par un calcul numérique et est optimale. C'est une manière classique de résoudre le problème chimique.
Méthode de porte quantique
Une méthode dans laquelle des bits quantiques sont incorporés dans un semi-conducteur pour le calcul. L'ordinateur quantique conventionnel fait souvent référence à cette méthode, mais avec l'avènement de l'ordinateur quantique pour le recuit quantique, la position a été inversée.
Cet ordinateur quantique de type porte quantique ne fonctionnait pas bien car l'état quantique était susceptible de s'effondrer.
Effet tunnel
Dans l'état quantique, une substance peut être considérée comme une onde, qui est une onde probabiliste qui, dans certaines circonstances, «traverse» plutôt que de surmonter les barrières énergétiques.
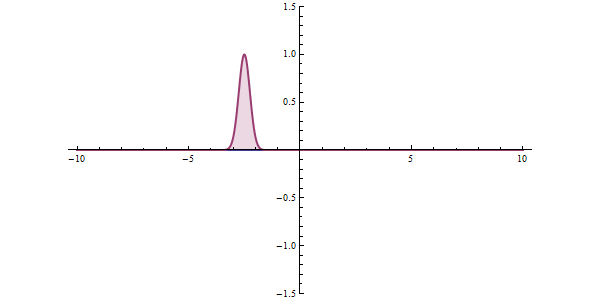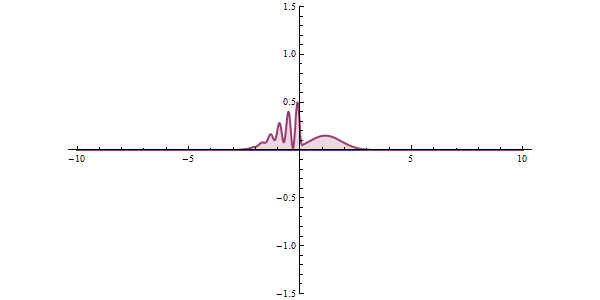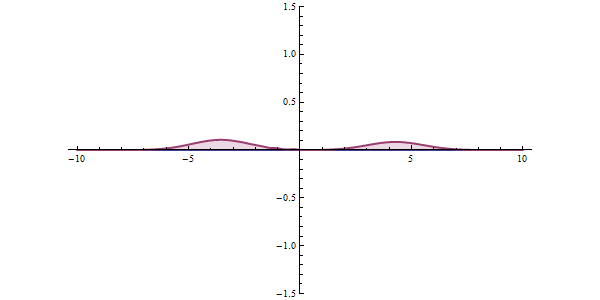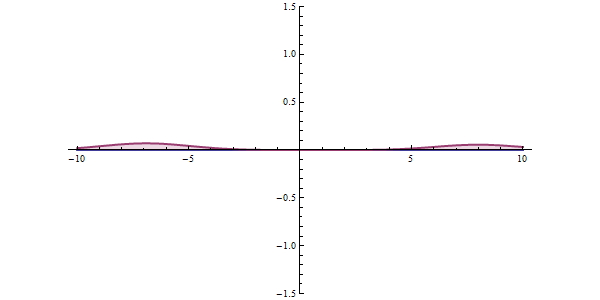
https://ja.wikipedia.org/wiki/%E3%83%88%E3%83%B3%E3%83%8D%E3%83%AB%E5%8A%B9%E6%9E%9C
tourner
C'est la plus petite unité d'un aimant. L'électron, qui est la plus petite unité de courant, a la propriété de rotation. Il s'agit de tourner. Exprimé comme (vers le haut, vers le bas) ou (vers la droite, vers la gauche)
~~ Il semble que les gens qui se spécialisent dans les particules élémentaires seront vraiment en colère (rires) ~~ Continuons sans nous en soucier
Modèle en hausse
C'est un modèle pour réaliser un recuit quantique, et il est possible de faire de l'état qui minimise l'état d'énergie de ce qui précède la solution du problème d'optimisation.
D-Wave
Une société qui a mis en pratique la théorie du professeur Nishimori, qui préconisait le recuit quantique, et a produit le premier ordinateur quantique commercial au monde.
À propos du problème du voyageur de commerce qui ne peut être résolu même avec un super ordinateur
Vendeur itinérant En considérant le problème, un vendeur considère l'itinéraire qui minimise la distance lorsqu'il traverse plusieurs villes.
Par exemple, trois villes (par exemple Tokyo, Nagoya et Osaka) Tokyo → Osaka → Nagoya → Tokyo et Tokyo → Nagoya → Osaka → Tokyo, Il semble que la direction opposée soit considérée comme la même, donc c'est 1 pour 3 villes.

Extrait de [Quantum Computer 1] Soudainement Commercialisé Dream Machine (3/6)
Généraliser
\frac{(n-1)!}{2}rue
est. Donc si vous l'écrivez en Python (je ne pense pas que vous ayez besoin de l'écrire)
#Problème de vendeur de patrouille
import math
def travelingSales(n):
return math.factorial(n-1)/2
Avec ça, 8 villes
travelingSales(8)
2520
Dans 15 villes
travelingSales(15)
43589145600.0(45,3 milliards)
Dans 20 villes
travelingSales(20)
6.0822550204416e+16
Dans 30 villes
travelingSales(30)
4.420880996869851e+30
…
Ce sera. Jusqu'à 20 villes peuvent être résolues en quelques secondes avec un superordinateur, mais 30 villes prendraient 14 millions d'années, ce qui est trop long.
Ce qui précède est un aperçu du problème du voyageur de commerce.
Référence: [Quantum Computer 1] Dream Machine soudainement commercialisé: ITpro
Alors que dois-je faire?
En pratique, il existe plusieurs façons de calculer diverses approximations pour résoudre le problème ci-dessus, mais je vais me concentrer sur le recuit simulé, qui est lié au recuit quantique.
Tout d'abord, si vous résumez brièvement la situation actuelle, il semble que les êtres humains peuvent comprendre un simple itinéraire le plus court, mais comme l'ordinateur doit se donner la peine de calculer l'itinéraire le plus court après avoir considéré toutes les combinaisons d'itinéraires, Même s'il y avait une trentaine de villes, l'itinéraire lui-même était innombrable et ne pouvait être résolu.
Afin d'expliquer un exemple concret, j'expliquerai en référence au document officiel de Scipy.
«Les problèmes d'optimisation sont des problèmes qui trouvent des solutions numériques aux valeurs minimales et aux équations. Le module scipy.optimize minimise les fonctions (scalaires et multidimensionnelles) et ajuste les courbes. Et il fournit un algorithme pratique pour la recherche racine. (Extrait du Document officiel)
Tracez le problème d'optimisation à l'aide de Optimize.fmin_bfgs en utilisant l'algorithme BFGS et calculez-le réellement.
Définissons la fonction suivante et résolvons réellement le problème d'optimisation.
f(x)=x^2+15sin(1.2x) \\ (-10\leqq x\leqq10)
from scipy import optimize
def minfunc(x):
return x**2+ 15*np.sin(1.2*x)
x = np.arange(-10, 10, 0.1)
plt.plot(x, minfunc(x))

Vous pouvez facilement le trouver en définissant Optimize.fmin_bfgs (fonction, valeur initiale, disp = 0).
#disp=0 ne donne que la valeur minimale
optimize.fmin_bfgs(minfunc, 0,disp=0)
La valeur obtenue est
array([-1.19776296])
Certes, la valeur minimale qui peut être visuellement reconnue a été obtenue.
Cependant, provisoirement dans le deuxième argument de Optimize.fmin_bfgs
#Valeur initiale x=-Définir sur 5
optimize.fmin_bfgs(minfunc, -5, disp=0)
array([-5.94383045])
#Valeur initiale x=Régler sur 3
optimize.fmin_bfgs(minfunc, 3, disp=0)
array([ 3.58552219])
#Valeur initiale x=Définir sur 10
optimize.fmin_bfgs(minfunc, 10, disp=0)
array([ 8.20653212])
Ensuite, ce sera comme ci-dessus.
À partir de la valeur initiale, seule la valeur de y lorsque le coefficient différentiel est 0 (l'endroit où la balle est coincée dans la bosse lorsque la balle est roulée à partir de l'endroit spécifié) peut être obtenue.

S'appliquant au problème du vendeur de patrouille, en supposant que la direction verticale du graphique est la distance qui patrouille dans la ville et que l'axe horizontal est le nombre de modèles qui patrouillent dans la ville (bien que cela semble un peu agressif), $ (-10 \ Pour tous les leqq x \ leqq10) $, prenez comme exemple Optimize.fmin_bfgs, essayez diverses valeurs initiales, et la valeur la plus basse est la valeur minimale (c'est-à-dire la valeur minimale de la distance parcourue autour de la ville). est.
Après tout, si vous le recherchez à fond, il sera difficile de le résoudre lorsqu'il atteindra 30 modèles comme le problème du voyageur de commerce.
Pour résoudre les problèmes ci-dessus, il existe une technique appelée recuit simulé.
Dans le recuit simulé, une distribution probabiliste est donnée, la distribution est agrandie dans un premier temps, puis la distribution des probabilités est progressivement rétrécie (ce travail est la partie où la température de la "cuisson" classique est progressivement abaissée. Même s'il est toujours piégé dans l'exemple ci-dessus (le coefficient différentiel est égal à 0), il ne termine pas le calcul à ce stade et va chercher la valeur minimale finale.
Cependant, même avec cette méthode, il semble que le calcul soit inférieur au calcul de compression, mais dans le cas d'un problème compliqué, une énorme quantité de calcul est nécessaire et une grande quantité d'énergie est nécessaire pour échapper au piège. sera nécessaire.

Dans le recuit quantique, cela est résolu par l '** effet tunnel **, qui est un phénomène quantique.
En plus de la recherche probabiliste de recuit simulé, en recherchant avec des ondes qui sont à l'état quantique, il est possible de créer un effet tunnel à partir de la position piégée et de passer facilement à la valeur minimale.
Comme décrit ci-dessus, il semble qu'il soit possible de calculer le problème du voyageur de commerce en utilisant l'effet quantique pour le recuit simulé classique. (Dans "L'ordinateur quantique accélère l'intelligence artificielle", il était écrit que ce serait "100 millions de fois".)
- L'effet tunnel est que si une certaine condition est remplie, la vague de particules suintera de manière probabiliste, il est donc peu probable que le tunnel tombe si facilement vers la solution optimale, mais la raison en est celle d'un individu. En guise de devoir, j'aimerais le savoir plus tard.
Modèle en hausse qui permet réellement le recuit quantique
Ensuite, en fait, il existe un «modèle ising» comme modèle pour résoudre la solution optimale dans la situation qui permet le recuit quantique.

En termes de taille atomique, la propriété du spin, qui est la plus petite unité d'un aimant, apparaît. En fait, il est petit et disjoint, il est donc généralement invisible, mais dans un état spécial, les spins sont alignés et, par conséquent, les propriétés d'aimant sont nées. (* L'étude du "magnétisme" dans le domaine des aimants est extrêmement difficile !!)
Cette propriété de rotation n'a que deux états, vers le haut et vers le bas. (Pour ceux qui savent, l'état énergétique de l'état quantifié ne peut prendre que des valeurs discrètes.)
Le modèle Zing est un modèle qui calcule en utilisant cette propriété de "spin" qui peut être vue quand elle est petite. (Je vais omettre l'histoire de l'interaction et la formule elle-même pour calculer le modèle d'Ising car c'est difficile.)
Je ne sais pas de quoi vous parlez dans l'explication jusqu'à présent, alors jetons un coup d'œil concret.
Pour simplifier le calcul, réduisez les dimensions et discutez en deux dimensions. (Bref, discutons dans le monde de l'animation sans profondeur.)
L'histoire originale est Je vais expliquer le modèle Ising d'une manière simple Et Simulation Monte Carlo du modèle Ising à l'aide de Python Puisqu'il est implémenté, reportez-vous à cela (en particulier, l'ancien code a été expliqué et amélioré).
Pour en faire une animation, j'utilise artistAnimation de matplotlib pour enregistrer plusieurs images dans le tableau ims et les déplacer avec ArtistAnimation. http://qiita.com/yubais/items/c95ba9ff1b23dd33fde2
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
from pandas import Series, DataFrame
from numpy.random import randint, randn, rand
import math
import matplotlib.animation as animation
#Jouer l'animation matplotlib sur Jupyter
%matplotlib nbagg
#Nombre d'atomes
Size = 50
#J est une constante représentant l'interaction entre les spins
J = 1
#champ magnétique
H = 0
#Température[K]
Temp = 0
#La rotation s'inverse-t-elle?
def spin_direction(field, x, y):
energy = H
'''
Condition aux limites périodique
(Parce que l'atome situé au bord n'est pas en contact avec les quatre atomes
Ce n'est que dans ce cas qu'il se déplace en parallèle.)
'''
for dx, dy in [(-1,0), (1,0), (0,-1), (0,1)]:
if x + dx < 0:
dx += Size
if y + dy < 0:
dy += Size
if x + dx >= Size:
dx -= Size
if y + dy >= Size:
dy -= Size
#Calcul énergétique
energy += J * field.iloc[x + dx, y + dy]
if Temp == 0:
#np.le signe est 1 pour le positif et 1 pour le négatif pour chaque élément-S'il vaut 1, 0, 0 est renvoyé.
p = (np.sign(energy) + 1) * 0.5
else:
#Probabilité d'inversion de spin avec la température et l'énergie (T=(Sauf quand c'est 0)
p = 1/(1+np.exp(-2*(1/Temp)*energy))
#Si le spin calculé ci-dessus a une probabilité d'inversion plus élevée qu'un nombre aléatoire à virgule flottante entre 0 et 1.
if rand() <= p:
spin = 1
else:
spin = -1
return spin
#Je ne sais pas grand-chose sur Gibbs Sampling.
def run_gibbs_sampling(field, iternum=5):
for _ in range(iternum):
lattice = DataFrame([(y,x) for x in range(Size) for y in range(Size)])
#La réindexation réassigne la position de l'atome de manière appropriée
lattice = lattice.reindex(np.random.permutation(lattice.index))
#lattice.values est la position de chaque point de la grille. Par exemple[0,0]Si tel est le cas, 0e verticalement et 0e horizontalement
for x, y in lattice.values:
#Calculez si la rotation est inversée
field.iloc[x, y] = spin_direction(field, x, y)
fig = plt.figure()
field = DataFrame(randint(2,size=(Size,Size))*2-1)
temps = [0.,.5,1.,1.5,2.,2.5,5.0,10.0][::-1]
ax1=fig.add_subplot(1,2,1)
ax2=fig.add_subplot(1,3,3)
ax2.axis(xmin=-1,xmax=10.5)
ax2.set_xlabel("time")
ax2.set_ylabel("T[K]")
ims = []
for i in range(1,9):
Temp = temps[i-1]
run_gibbs_sampling(field)
im1 = ax1.imshow(field.values, vmin=-1, vmax=1,cmap=plt.cm.gray_r, interpolation='nearest')
x=np.arange(1, 9, 1)
im2,=ax2.plot(x[0:i], temps[0:i],marker="o",markersize=12,color = "red")
ims.append([im1,im2])
ani = animation.ArtistAnimation(fig, ims, interval = 1000)
#Enregistrer la destination (si nécessaire)
#ani.save("ising.gif")
plt.show()

Lorsque la température s'approche de 0K (la température absolue est de -273,15 $ {} ^ \ circ \ mathrm {C} $ est de 0K), les états de spin disjoints deviennent stables (c'est-à-dire les états de basse énergie). Vous pouvez voir comment les directions ascendante et descendante sont localisées.
Le véritable état stable est que tout est en haut ou en bas, mais il se trouve être côte à côte lorsque la température baisse car il était probablement disjoint (plus précisément, disjoint par la vibration des atomes due à la température). Certains des spins sont localisés car ils ont la propriété de pointer dans la même direction.
- L'interaction de spin est déterminée par la taille de J.
Lorsqu'un champ magnétique est appliqué (en supposant que l'aimant est rapproché), il suffit d'exécuter (H = 0,5 dans le code ci-dessus).

Ici, en raison de la force du champ magnétique, ils font tous face à la même direction près de T = 2K.
Comme précédemment, vous pouvez voir que les choses qui se sont avérées localisées sont toutes orientées dans la même direction avant d'être localisées à l'aide du champ magnétique.
Jusqu'à présent, nous avons expliqué le modèle d'inging bidimensionnel. (C'était long.)
Selon ce modèle, le recuit quantique est une application du problème d'optimisation qui applique effectivement l'état stable du spin d'une substance.
L'ordinateur quantique réel est une extension tridimensionnelle du modèle ascendant ci-dessus. S'étendant à ce modèle, le spin n'a mystérieusement que deux états, haut et bas.
En appliquant un champ magnétique latéral à une substance qui est une extension tridimensionnelle du modèle de Zing, un état de superposition ascendante et descendante (état d'enchevêtrement quantique) de spins est créé.
Si le champ magnétique transversal est progressivement diminué de la même manière que la température a été abaissée précédemment, l'interaction de spin entre les atomes devient plus grande, et l'état d'énergie de spin lorsque le champ magnétique transversal est de 0 est la valeur minimale à résoudre. Prendre.
Comme décrit ci-dessus, en effectuant l'état de superposition (intrication quantique) des spins avec un matériau réel, même en recuit simulé, le problème d'optimisation qui nécessitait une énorme quantité de calcul peut être résolu par le phénomène quantique (en particulier tunnel). Il est réalisé par l'effet).
J'ai essayé de dessiner moi-même une figure, mais j'étais épuisée. Pour plus de détails, consultez le site que j'ai présenté plus tôt. (Peut être modifié et mis à jour plus tard) http://itpro.nikkeibp.co.jp/article/COLUMN/20140514/556566/
Est-ce lié au machine learning et au deep learning?
Il devrait être appliqué dans les domaines de l'apprentissage automatique et de l'apprentissage profond, et de l'IA (ou apprentissage automatique) qui s'est rapidement développé ces dernières années, tels que les problèmes d'optimisation de portefeuille d'investissement, l'authentification d'image, les soins médicaux, le droit et l'archéologie. Dans le domaine des, cet ordinateur quantique semble être capable de les accélérer. De plus, avec l'avènement de l'onde D, Google essaie sérieusement de réaliser un ordinateur quantique avec cette méthode, et on peut dire que les domaines d'application par recuit quantique sont très divers. (Pour plus de détails sur ce domaine, veuillez vous référer à "Quantum Computer Accelerates Artificial Intelligence" du professeur Nishimori.)
À la fin
En tant que rétrofit, je travaille actuellement en tant que data scientist pour analyser le big data (principalement des données Web) à l'aide de l'IA (apprentissage automatique ou statistiques), mais je suis une école supérieure. Donc, je recherchais un élément appelé transistor de spin qui réalise un ordinateur quantique de type porte quantique.
Il était surprenant que l'intelligence artificielle et les ordinateurs quantiques, que l'on pensait sans rapport à l'époque, aient commencé à établir une relation ces dernières années et que les ordinateurs quantiques jouent un rôle important dans la réalisation d'une véritable IA. (La recherche universitaire n'a pas été gaspillée.)
De plus, la mécanique quantique et les modèles d'ingénierie sont encore très profonds, j'ai donc décidé de profiter de cette occasion pour étudier davantage. (Maintenant, j'étais frustré à ce moment-là [Physique statistique de Randau](https://www.amazon.co.jp/%E7%B5%B1%E8%A8%88%E7%89%A9%E7%90%86] % E5% AD% A6-% E4% B8% 8A-% E3% 82% A8% E3% 83% AA% E3% 83% BB% E3% 83% A9% E3% 83% B3% E3% 83% 80 Vous devriez pouvoir lire% E3% 82% A6 / dp / 4000057200) (rires)
Le spin, la mécanique quantique et la mécanique statistique sont des disciplines qui discutent du micro-monde et ne peuvent être comprises en un jour ou deux. Si vous saisissez cette occasion pour étudier diverses choses, vous devriez être en mesure de comprendre le plaisir et l'attention. (À l'origine, ce livre était numéro un dans la catégorie physique d'Amazon.)
* En tant que problème individuel
-Une vue d'ensemble rigoureuse de la manière dont l'effet tunnel permet d'atteindre plus facilement la solution optimale que le recuit simulé traditionnel.
・ À propos de l'échantillonnage Gibbs
Je veux comprendre ce qui précède et réécrire un article (rires)
De plus, si vous avez des erreurs ou des questions évidentes, veuillez nous en informer. Je le réparerai.
Recommended Posts