Utiliser l'optimisation des combinaisons
introduction
Je vais vous expliquer le savoir-faire pour utiliser l'optimisation des combinaisons.
L'astuce pour utiliser l'optimisation combinée est d'avoir une vue d'ensemble. En sachant quels sont les éléments et comment ils se rapportent les uns aux autres, vous pourrez aborder le problème que vous souhaitez résoudre. Vous pouvez facilement effectuer diverses optimisations en utilisant Python. Vérifions-le plus tard en regardant le code réel. Tout d'abord, regardons un exemple d'optimisation familière.
Réfléchissons
L'autre jour, de retour chez vous, on vous a dit d'apporter des légumes en souvenir. Les légumes à Tokyo sont chers, donc j'étais ravi qu'ils soient «rentables», mais la quantité était trop importante. Supposons que vous ne puissiez rapporter que 5 kg au maximum. (Veuillez ne pas utiliser de messagerie) De plus, les légumes seront endommagés s'ils sont coupés, je les ramènerai donc à la maison tels quels.
Vous vous êtes dit: "Choisissons parmi ceux dont le prix de vente par kg est le plus élevé." En fait, ce n'est pas la meilleure méthode (bien que ce soit une solution approximative rapide et efficace appelée méthode gloutonne). Comment connaissez-vous le meilleur moyen?
Si vous regardez toutes les possibilités, vous saurez comment optimiser. Cependant, toutes les combinaisons de légumes exploseront à mesure que le nombre de légumes augmentera et ne pourront pas être calculées. ** L'optimisation mathématique ** peut être utilisée pour résoudre de tels problèmes. L'optimisation mathématique utilise des formules mathématiques pour représenter le problème avec un ** modèle mathématique **. L'exemple précédent est
| $ \ sum_i {w_i x_i} \ le 5 $ | $ w_i $: Poids | |
| $ \ forall x_i \ in \ {0, 1 \} $ | $ x_i $: s'il faut le ramener à la maison > |
| Optimisation continue: | Éléments continus uniquement |
| Optimisation de combinaison: | contient des éléments discrets non continus |
Formulation
Leçon 1
** En optimisation combinée, un modèle mathématique est formulé. ** **
Pour formuler, nous devons déterminer trois facteurs.
| 1. Que voulez-vous décider? | "Je veux décider quels légumes ramener" |
| 2. Que souhaitez-vous faire? | "Je suis content si le prix de vente total des légumes que je ramène est plus élevé" |
| 3. Que dois-je protéger? | "Peser moins de 5 kg de légumes à rapporter" |
| 1. Variables: | $ \ forall x_i \ in \ {0, 1 \} $ | |
| 2. Fonction objectif: | $ \ sum_i {p_i x_i} $ | $ \ rightarrow $ maximum |
| 3. Contraintes: | $ \ sum_i {w_i x_i} \ le 5 $ |
Il faut un certain temps pour être en mesure de formuler. Cette fois, nous examinerons quelques exemples plus tard. Si vous souhaitez étudier en détail, veuillez vous référer au livre "Peut être utilisé à partir d'aujourd'hui! Optimisation combinée". Pour trouver la meilleure réponse à partir d'un modèle mathématique, utilisez un outil (fabriqué par un homme sage). Cet outil est appelé un solveur optimisé, ou ** solveur ** pour faire court. En d'autres termes, vous pouvez simplement représenter le problème (afin que tout le monde puisse le comprendre) et utiliser le solveur pour trouver une solution (la réponse). De nos jours, ce solveur est facile à utiliser et ses performances se sont beaucoup améliorées. Tout le monde commence à essayer l'optimisation.
Problème typique
Quels autres exemples existe-t-il en plus des précédents? Vous avez peut-être recherché une station de transfert sur le Web lorsque vous êtes rentré chez vous.
Je veux trouver le trajet le plus court (ou le moins cher) de la gare la plus proche de chez toi à la gare la plus proche du domicile de tes parents.
C'est également un problème d'optimisation. Il existe de nombreux problèmes d'optimisation dans de nombreux endroits. Cependant, il est difficile de formuler chaque problème. En fait, différents problèmes ont souvent la même formulation. De cette façon, vous n'avez pas à vous soucier de le formuler, ce qui est pratique. Nous appellerons les problèmes courants dans le monde ** problèmes typiques **.
Leçon 2
** Comprendre les problèmes typiques. ** **
Collectez les problèmes typiques associés et créez un cadre appelé ** classe de problème typique **. Il existe sept classes de problèmes typiques. Pour les problèmes typiques, nous avons soigneusement sélectionné les plus couramment utilisés.
| Classe de problème typique | Problème typique |
| Problème de réseau de graphes | Problème minimal d'arborescence de surface entière |
| Problème de jeu stable maximum | |
| Problème de coupe maximum | |
| Problème de couverture minimale des sommets | |
| Problème d'itinéraire le plus court | |
| Problème de débit maximum | |
| Problème de flux de coût minimum | |
| Problème de route | Problème de route de transport |
| Problème de vendeur de patrouille | |
| Problème de couverture agrégée / division | Problème de couverture agrégée |
| Problème de division de groupe | |
| Problème de planification | Problème d'atelier de travail |
| Problème de planification du travail | |
| Problème de coupure / blocage | Problème de sac à dos |
| Problème d'emballage du bac | |
| problème d'emballage en n dimensions | |
| Problème de placement | Problème de placement d'installation |
| Pas de contrainte de capacité Problème de placement des installations | |
| Problème d'allocation / correspondance | Problème d'allocation secondaire |
| Problème d'allocation généralisé | |
| Problème de correspondance maximum | |
| Problème de correspondance de poids | |
| Problème de correspondance stable |
Comment choisir les légumes s'appelle ** problème de sac à dos **, et la recherche de station de transfert s'appelle ** problème d'itinéraire le plus court **. Les problèmes typiques sont bien étudiés et ont souvent des solutions efficaces. Alternativement, il est formulé de manière à pouvoir être résolu immédiatement. Faisons-le plus tard. Voir Problèmes typiques et méthodes d'exécution pour des exemples d'exécution de tous les problèmes typiques répertoriés ici.
Problème général
Je vais parler du travail sur les conteneurs que je fais ces derniers temps. C'est grâce au transport de conteneurs que les gens du monde entier peuvent acheter diverses choses à bon marché. En effet, les produits fabriqués en Chine peuvent être expédiés au Japon, aux États-Unis et en Europe en grandes quantités à bas prix. Cependant, les conteneurs vides sont de plus en plus empilés. Je dois retourner en Chine. Déterminer quand, où et où retourner est le ** problème de flux de coût minimum **. Cependant, il existe certaines contraintes qui ne peuvent être exprimées par le problème de flux de coût minimum. L'un s'appelle le cabotage. Le cabotage doit réglementer le transport intérieur uniquement vers les entreprises nationales. Si le problème typique ne peut pas être traité, le modèle mathématique est traité tel quel. Le problème représenté par le modèle mathématique est appelé ** problème général **. Les problèmes typiques peuvent également être considérés comme des problèmes d'ordre général. Les problèmes d'ordre général sont une classification plus générale que les problèmes typiques.
Lecon 3
** Comprendre les problèmes génériques. ** **
Quels sont les problèmes généraux?
Les différences dans les problèmes à usage général sont dues à des différences de variables, de fonctions objectives et de contraintes. Différents problèmes à usage général ont des solutions (algorithmes) différentes. La facilité de résolution est complètement différente selon le type de cette solution. En outre, chaque problème générique peut avoir un solveur différent. Dans la mesure du possible, il est important de pouvoir l'amener à un problème à usage général qui peut être facilement résolu. Le problème général est une relation parent-enfant.

Tous les problèmes d'optimisation sont des problèmes d'optimisation non linéaires. Pourquoi s'embêter avec l'optimisation non linéaire? En effet, il est inefficace de traiter le problème d'optimisation linéaire comme une optimisation non linéaire. Le terme d'optimisation non linéaire suggère implicitement qu'il existe une fonction objectif non linéaire ou une contrainte non linéaire.
** Problème d'optimisation linéaire **
Le problème généraliste le plus simple à résoudre est le problème d'optimisation linéaire. Le problème du flux de coût minimum et le problème de l'itinéraire le plus court sont également des problèmes d'optimisation linéaire. Il s'agit d'un problème dans lequel la variable est une variable continue et la fonction objectif et la condition de contrainte sont exprimées linéairement (expression linéaire). Cela a permis de résoudre des problèmes même assez importants.
** Problème d'optimisation d'entiers mixtes **
La fonction objectif et les contraintes sont linéaires, mais les problèmes qui incluent des variables entières (seuls les entiers sont autorisés) dans les variables sont appelés problèmes d'optimisation d'entiers mixtes. Le problème du sac à dos est également un problème d'optimisation des nombres entiers mixtes. C'est un problème courant dans la pratique et bon nombre des problèmes auxquels je suis confronté. C'est un problème difficile, mais il est récemment devenu possible de le résoudre en fonction de la formulation et de l'ampleur du problème. «Nous sommes désormais en mesure de résoudre des problèmes d'optimisation en nombres entiers mixtes.» C'est la raison pour laquelle le seuil d'optimisation a été abaissé. Pour les débutants en optimisation mathématique, un objectif sera de formuler un simple problème d'optimisation en nombres entiers mixtes. Cependant, en pratique, traiter des problèmes d'optimisation en nombres entiers mixtes peut être difficile et demander une certaine ingéniosité.
** Problème d'optimisation non linéaire **
L'optimisation non linéaire est un problème encore plus difficile. Cependant, s'il s'agit d'une petite échelle, il peut être résolu même à l'heure actuelle. De plus, parmi l'optimisation non linéaire, l'optimisation convexe non linéaire peut être gérée même à grande échelle, mais elle est omise ici.
Nous verrons ces trois exemples plus tard.
Relation entre les problèmes typiques et les problèmes généraux
Tous les problèmes d'optimisation mathématique sont soit des problèmes à usage général. Les problèmes d'ordre général peuvent être considérés comme une catégorie majeure de problèmes d'optimisation de combinaison. Cependant, cette classification est trop approximative. La classification des organismes est semblable aux vertébrés et aux invertébrés. Un problème typique peut être considéré comme une sous-classe. En termes d'êtres vivants, sont-ils des insectes et des mammifères? Il sera plus facile à retenir car vous pouvez ressentir le problème typique de plus près.

- Une classe de problème typique peut contenir différents problèmes génériques. ――La formulation peut être considérée comme un dessin de conception similaire à l'ADN dans les organismes vivants. Cependant, même si un organisme n'a qu'un seul ADN, un problème peut être considéré comme un problème distinct. ――Le solveur (c'est-à-dire la solution) change en fonction de la façon dont vous le considérez comme un problème général ou un problème typique.
- En général, les résolveurs de problèmes typiques sont plus efficaces que les résolveurs de problèmes généraux.

Je compléterai le problème général. Bien que les vertébrés et les invertébrés des organismes vivants soient des groupes distincts, ils sont fondamentalement inclusifs dans la classification des problèmes généraux. Autrement dit, tous les problèmes sont des problèmes d'optimisation non linéaires, parmi lesquels des problèmes d'optimisation d'entiers mixtes, et parmi eux des problèmes d'optimisation linéaire. En d'autres termes, le problème d'optimisation linéaire est à la fois un problème d'optimisation en nombres entiers mixtes et un problème d'optimisation non linéaire. Le problème d'optimisation d'entiers mixtes est également un problème d'optimisation non linéaire. Ceci est également vrai lors de l'application de solveurs. Autrement dit, le solveur d'optimisation non linéaire peut gérer tous les problèmes d'optimisation non linéaire, les problèmes d'optimisation en nombres entiers mixtes et les problèmes d'optimisation linéaire. Le solveur d'optimisation d'entiers mixtes ne peut pas gérer les problèmes d'optimisation non linéaires généraux, mais peut gérer les problèmes d'optimisation d'entiers mixtes et les problèmes d'optimisation linéaire. Le solveur d'optimisation linéaire ne peut gérer que des problèmes d'optimisation linéaire. Par convention, les solveurs d'optimisation en nombres entiers mixtes et les solveurs d'optimisation linéaire sont souvent combinés en un seul solveur.
Certains solveurs d'optimisation non linéaires peuvent et ne peuvent pas prendre des contraintes, mais pour les praticiens, il semble suffisant de ne s'occuper que des solveurs qui peuvent prendre des contraintes, donc nous supposons ici que les contraintes peuvent être prises en compte. Je suis.
Les solveurs fonctionnent mieux dans les zones plus petites. Pour les problèmes d'optimisation linéaire, il est plus rapide d'obtenir la solution optimale en utilisant le solveur d'optimisation linéaire. L'utilisation d'un solveur d'optimisation non linéaire pour un problème d'optimisation linéaire présente des inconvénients tels que «il est nécessaire de spécifier une solution initiale» et «cela prend un temps de calcul énorme».
Il existe une classification beaucoup plus fine parmi les chercheurs en optimisation, mais pour de nombreux praticiens, trois types suffisent: l'optimisation non linéaire, l'optimisation d'entiers mixtes et l'optimisation linéaire. Le problème d'optimisation des entiers mixtes est également appelé problème d'optimisation linéaire des entiers mixtes. Les chercheurs appellent l'optimisation linéaire LP (programmation linéaire), l'optimisation d'entiers mixtes MIP ou MILP (programmation linéaire en nombres entiers mixtes) et l'optimisation non linéaire NLP (programmation non linéaire). La programmation était à l'origine traduite par «planification», mais récemment, elle est devenue l'optimisation, nous l'avons donc unifiée avec l'optimisation ici aussi. Puisque l'optimisation est l'optimisation, la façon dont elle est appelée peut changer à l'avenir.
Exemple d'exécution d'un problème typique par Python
Leçon 4
** Essayons-le. ** **
** Problème de sac à dos **
Mettez des bagages dans le sac à dos. Maximisez la somme des poids des bagages afin que la somme des tailles des bagages à emballer ne dépasse pas la capacité du sac à dos.
python
from ortoolpy import knapsack
size = [21, 11, 15, 9, 34, 25, 41, 52]
weight = [22, 12, 16, 10, 35, 26, 42, 53]
capacity = 100
knapsack(size, weight, capacity)
>>>
(105, [0, 1, 3, 4, 5])
Vous obtiendrez la somme des valeurs des packages sélectionnés (105) et l'ordre des packages sélectionnés ([0, 1, 3, 4, 5]).
** Problème de route le plus court **
Dans le graphique, recherchez l'itinéraire le plus court entre le point de départ et le point d'arrivée.
python
import networkx as nx
g = nx.fast_gnp_random_graph(8, 0.26, 1)
nx.dijkstra_path(g, 0, 2)
>>>
[0, 1, 6, 3, 5, 2]
Créez un graphique aléatoire de 8 points pour obtenir une liste des chemins les plus courts du nœud 0 au nœud 2 ([0, 1, 6, 3, 5, 2]).
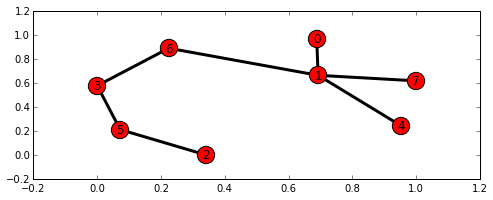
Pour d'autres exemples typiques d'exécution de problèmes, consultez Problèmes typiques et méthodes d'exécution.
Exemple d'exécution d'un problème général en utilisant Python
Pour savoir comment utiliser PuLP, voir [Comment créer un problème général avec PuLP](# pulp% E3% 81% A7% E3% 81% AE% E6% 95% B0% E7% 90% 86% E5% 95% 8F% E9 Veuillez vous référer à% A1% 8C% E3% 81% AE% E4% BD% 9C% E3% 82% 8A% E6% 96% B9).
** Problème de sac à dos **
Mettez des bagages dans le sac à dos. Maximisez la somme des poids des bagages afin que la somme des tailles des bagages à emballer ne dépasse pas la capacité du sac à dos.
python
from pulp import *
size = [21, 11, 15, 9, 34, 25, 41, 52]
weight = [22, 12, 16, 10, 35, 26, 42, 53]
capacity = 100
r = range(len(size))
m = LpProblem(sense=LpMaximize) #Modèle mathématique
x = [LpVariable('x%d'%i, cat=LpBinary) for i in r] #variable
m += lpDot(weight, x) #Fonction objective
m += lpDot(size, x) <= capacity #Contrainte
m.solve()
print((value(m.objective), [i for i in r if value(x[i]) > 0.5]))
>>>
(105.0, [0, 1, 3, 4, 5])
Le problème du sac à dos est un problème d'optimisation d'entiers mixtes pour des problèmes généraux.
** Problème de route le plus court **
Dans le graphique, recherchez l'itinéraire le plus court du point de départ au point d'arrivée.
python
from pulp import *
import networkx as nx
g = nx.fast_gnp_random_graph(8, 0.26, 1).to_directed()
source, sink = 0, 2 #point de départ,point final
r = list(enumerate(g.edges()))
m = LpProblem() #Modèle mathématique
x = [LpVariable('x%d'%k, lowBound=0, upBound=1) for k, (i, j) in r] #variable(S'il faut entrer sur la route)
m += lpSum(x) #Fonction objective
for nd in g.nodes():
m += lpSum(x[k] for k, (i, j) in r if i == nd) \
== lpSum(x[k] for k, (i, j) in r if j == nd) + {source:1, sink:-1}.get(nd, 0) #Contrainte
m.solve()
print([(i, j) for k, (i, j) in r if value(x[k]) > 0.5])
>>>
[(0, 1), (1, 6), (3, 5), (5, 2), (6, 3)]
Le problème de chemin le plus court est un problème d'optimisation linéaire pour les problèmes à usage général. Pour le problème du chemin le plus court, il existe une solution efficace appelée méthode Dyxtra. Il n'est pas recommandé de le résoudre en tant que problème à usage général. La méthode Dyxtra est [Exemple d'exécution d'un problème typique par Python](# python-% E3% 81% AB% E3% 82% 88% E3% 82% 8B% E6% A8% 99% E6% BA% 96% E5% 95% 8F% E9% A1% 8C% E3% 81% AE% E5% AE% 9F% E8% A1% 8C% E4% BE% 8B) Utilisé dans l'exemple (nx.dijkstra_path).
** Problème d'optimisation du portefeuille **
Déterminez le pourcentage ($ x_i
) pour acheter l'action. Minimiser le risque (diversification ( v_i $)) sous réserve de la limite inférieure de retour sur investissement (t / yen). Cependant, chaque numéro sera indépendant.
python
import numpy as np, scipy.optimize as so
p = [31, 86, 29, 73, 46, 39, 58] #Profit/Cercle
v = [10, 60, 25, 50, 35, 30, 40] #Distribué/Cercle
t = 50 #Bénéfice cible/Cercle
so.fmin_slsqp(lambda x: sum(v*x*x), np.zeros(len(p)),
eqcons=[lambda x: sum(x) - 1], ieqcons=[lambda x: sum(p*x) - t])
>>>
Optimization terminated successfully. (Exit mode 0)
Current function value: 4.50899167487
Iterations: 14
Function evaluations: 136
Gradient evaluations: 14
array([ 0.26829785, 0.13279566, 0.09965076, 0.1343941 , 0.11783349,
0.11506705, 0.13196109])
Le problème d'optimisation de portefeuille est un problème d'optimisation non linéaire pour les problèmes à usage général.
Réseau de graphes
Il existe de nombreux problèmes de réseau de graphes dans les problèmes d'optimisation combinée. C'est important, je vais donc le présenter brièvement ici. Un graphe est une structure composée de points et d'arêtes reliant les points. Il est souvent utilisé pour représenter de manière abstraite des relations réelles.
$ G = (V, E) $ signifie que "le graphe (G) est composé d'un ensemble de points (V) et d'un ensemble d'arêtes (E)". Un graphe à sens unique est appelé un graphe orienté, et un graphe avec d'autres côtés est appelé un graphe non orienté. Une série d'arêtes d'un point à un autre s'appelle un chemin. La connexion entre les points de départ et d'arrivée de l'itinéraire est appelée une route fermée. Un réseau est un système qui considère le flux de quelque chose sur le côté du graphe. Il existe des réseaux routiers, des réseaux de communication, etc.
Installation du logiciel
Nous vous recommandons d'utiliser Anaconda comme moyen facile à installer. Pour installer Anaconda, téléchargez le programme d'installation depuis Site et exécutez-le.
Anaconda comprend Python lui-même et de nombreux packages pour les calculs scientifiques et technologiques. Outre Anaconda, le logiciel nécessaire est PuLP, qui est un modélisateur d'optimisation mathématique et une bibliothèque pour les problèmes typiques.
--PuLP est installé avec "pip install pulp".
- L'installation de la bibliothèque pour les problèmes typiques est "pip install ou toolpy".
Comment créer un problème général avec PuLP
- Importer la bibliothèque
- from pulp import * --Création d'un modèle mathématique --Pour les problèmes de minimisation: m = LpPrblem () --Pour les problèmes de maximisation: m = LpProblem (sense = LpMaximize) --Création de variables --Variable continue: x = LpVariable (nom de la variable, lowBound = 0) --0-1 Variable: x = LpVariable (nom de la variable, cat = LpBinary) --Liste des variables continues: x = [LpVariable (i-ième nom de variable, lowBound = 0) pour i dans la plage (n)]
- Assurez-vous que les noms des variables sont différents
- Réglage de la fonction objectif --m + = expression
- Ajout de conditions de contrainte --m + = expression == expression --m + = expression <= expression --m + = expression> = expression --Exemple d'expression
- 2 * x + 3 * y - 5 --Sum: lpSum (liste des variables)
- Produit intérieur: lpDot (liste des coefficients, liste des variables) --Exécuter le solveur
- m.solve() --Valeurs des variables, expressions et fonctions objectives --valeur (variable), valeur (expression), valeur (m.objectif)
référence
- Python dans l'optimisation
- Power of Combinaison Optimisation Solver --M. Miyashiro Memo of Integer Planning
Points à noter
Il y a quelques points à garder à l'esprit lors de l'utilisation de l'optimisation dans la pratique. Les techniques d'optimisation actuelles ne peuvent pas entièrement modéliser les défis du monde réel. Vous ne pouvez pas le résoudre sans simplifier le modèle en tronquant les parties les moins importantes.
Par conséquent, le résultat de l'optimisation n'est souvent pas utilisable tel quel. Dans ce cas, il est important de vérifier pour voir quel est le problème. Comment afficher les résultats est également important pour trouver rapidement le problème.
Pour approfondir la compréhension
Voici quelques mots clés pour une étude plus approfondie.
- Montant du calcul, notation d'ordre, classe P, classe NP
- Recherche d'opérations, modélisation, méta-Huristique, dualité, problèmes d'atténuation, intelligence artificielle, apprentissage automatique, théorie des jeux
- Société académique connexe
- Société de recherche opérationnelle
- Applied Mathematical Society
- Thèmes d'optimisation et explications
- Domaine mathématique d'optimisation de l'Université de Kyoto (Laboratoire d'optimisation mathématique)
- Modèle mathématique --wikipedia
- Modélisation et optimisation des systèmes sociaux - Illustration de la situation critique
- Résolution de problèmes et mathématiques-Mathématiques filles
- À quoi faut-il faire attention lorsqu'on "comprend" un système complexe avec un modèle mathématique - Mode par défaut
De côté
Dans les organismes vivants, les deux nomenclatures de Linne (par exemple, Homo sapiens pour les êtres humains) sont courantes, mais même en optimisation, la façon de penser des problèmes à usage général et des problèmes typiques peut être similaire à celle-ci.
Le solveur changera selon qu'il s'agit d'un problème général ou d'un problème typique, mais c'est à l'utilisateur de faire un choix. À l'avenir, il sera peut-être possible de déterminer automatiquement. En d'autres termes, si vous le donnez au solveur en tant que problème à usage général, et si vous l'analysez et constatez qu'il s'agit d'un des problèmes typiques, vous pouvez automatiquement utiliser une solution plus efficace.
Connaissez-vous Higashi Robo-kun?
Il s'agit d'un projet de recherche mené par l'Institut national d'informatique, avec pour thème "Les robots peuvent-ils entrer à l'Université de Tokyo?".
En fait, l'approche d'optimisation basée sur des problèmes typiques est similaire à celle de Torobo-kun. Il s'agit de résoudre une grande variété de problèmes sous forme de problèmes typographiques. En regardant cette tentative, il semble que le jour viendra où il sera possible d'optimiser et de résoudre automatiquement les problèmes simplement en écrivant le problème en japonais.
Mais d'ici là, vous devrez penser par vous-même et bouger vos mains. De plus, ce faisant, vous apprendrez progressivement à gérer des problèmes plus complexes.
Recommended Posts