Créez DNN-CRF avec Chainer et reconnaissez la progression des accords de la musique
C'est le 11ème jour du Calendrier de l'Avent Chainer.
Qu'est-ce que la reconnaissance de la progression du code?
Lorsque nous faisons de la musique, nous pouvons obtenir un son plus riche en superposant des sons de différentes hauteurs. C'est ce qu'on appelle un accord. En changeant (en développant) les accords au fil du temps, la colonne vertébrale de la musique est complétée. C'est la progression du code. La progression d'accords est probablement le facteur le plus important lors de la copie de musique. Si vous connaissez la progression d'accords, vous pouvez presque reproduire l'accompagnement à la guitare ou au clavier. Eh bien, en bref, le texte consiste à laisser l'ordinateur copier automatiquement les oreilles. En copiant les oreilles, je ferai un jugement approximatif tel que "Je sonne dans cette mesure, et C est le suivant ...". Je ne pense pas à l'énumération des notes ou au rythme. Les accords peuvent être clairement définis par les sons constituants, mais lorsque le signal musical réel est décomposé dans la gamme de fréquences, la hauteur n'est pas claire, les harmoniques sont mélangées et les sons non constituants sont généralement mélangés, il n'est donc pas facile de les distinguer. Par conséquent, la situation actuelle est que nous avons tendance à nous appuyer sur des méthodes basées sur les données. C'est l'une des tâches de base dans le domaine du traitement des informations musicales (MIR) et est utile pour la discrimination de genre, l'analyse des émotions et la reconnaissance des chansons de reprise. C'est également l'une des missions du concours annuel de traitement de l'information musicale MIREX. MIREX 2016:Audio Chord Estimation Résumé des algorithmes participants Eh bien, c'est un problème d'étiquetage de série normal qui est formellement normal, donc j'espère que ce sera une référence pour la mise en œuvre de diverses tâches similaires, sans se limiter à la reconnaissance de la progression du code. L'implémentation de NN utilise Chainer, librosa pour le prétraitement et mir_eval pour calculer le taux de réponse correct.
Prétraitement d'entrée
L'entrée de NN est la série spectrale (ou spectrogramme) du signal musical. Si la procédure comprend un prétraitement,
- Séparez les composants de l'instrument de percussion du signal musical. Désactivons les sons des instruments de brouillage. C'est un coup avec librosa.
- Transformation Constant-Q. En parlant de conversion de spectre, il s'agit de la transformation de Fourier (STFT), mais la transformation de Fourier pose le problème que «la gamme de fréquences est linéaire» et «la résolution est différente pour chaque fréquence (car la fenêtre a une longueur fixe)». Puisque les informations de hauteur sont importantes pour les signaux musicaux, il est souhaitable de les afficher dans la plage de fréquences logarithmique. Il est possible de compresser le spectre FFT et de le convertir en plage de fréquences logarithmique, mais ici nous utilisons CQT, qui change la longueur de la fenêtre pour chaque fréquence afin que la résolution ne change pas. ~~ Quoi qu'il en soit, la librosa est un plan. ~~ 24 dimensions pour chaque octave (c'est-à-dire 1/2 demi-ton pour chaque dimension), et le spectre pour 6 octaves a été calculé à partir de la hauteur de C0, il s'agit donc d'un vecteur de 144 dimensions. Le choix des nombres est plutôt approprié.
- Compression logarithmique. Convertir en f (X) = log (1 + X). Il s'agit d'un prétraitement qui convertit la valeur vectorielle en une plage logarithmique pour supprimer le bruit. Cela semble un peu robuste.
- Concaténez les vecteurs adjacents en un vecteur plus grand. Par exemple, s'il y a un vecteur de temps t, un total de 7 vecteurs de t-3 à t + 3 (remplissage si pas assez) sont concaténés et convertis en un vecteur d'entrée de dimension 1008 (= 144x7). La taille d'entrée gonfle également 7 fois, mais la reconnaissance semble être plus stable. (* Voir aussi le supplément à la fin de la phrase!) Maintenant, jetons cette série vectorielle unidimensionnelle (un ensemble plutôt qu'une série pour DNN) dans DNN.
Modèle DNN-CRF
Créez un NN pour apprendre l'étiquetage de la série de spectre. C'est une dimension qui classe chaque trame par DNN, l'envoie à CRF, prend en compte le contexte de la série d'étiquettes, trouve la plausibilité de la série et sort la série d'étiquettes finale. Écrivons NN. Puisque la version Chainer utilise CRF, il ne devrait y avoir aucun problème si elle est 1.13 ou supérieure. Python est la série 2.7. Puisque nous voulons pouvoir contrôler facilement le nombre de couches cachées et le nombre d'unités, nous utilisons ChainList pour définir DNN. Eh bien, c'est juste une pile normale de couches entièrement connectées. La méthode d'apprentissage est la même que celle de l'exemple MNIST, aucune explication n'est donc nécessaire.
dnn.py
class DNN(ChainList):
def __init__(self,links):
super(DNN,self).__init__(*links)
self.train = True
def __call__(self,x):
links = self.children()
h = x
for i in xrange(self.__len__()-1):
li = links.next()
h = F.dropout((F.relu(li(h))),train=self.train)
y = links.next()(h)#La dernière étape est la conversion linéaire
return y
Et la définition de CRF. Ce qui est implémenté dans Chainer est un modèle appelé CRF à chaîne linéaire, qui semble être populaire dans le traitement du langage naturel, avec seulement l'étiquette précédente comme original. Prend la sortie de DNN comme entrée.
DNN.py
class CRF(Chain):
def __init__(self):
super(CRF,self).__init__(crf=L.CRF1d(N_CLASSES))
def __call__(self,list_x,list_t):
self.loss = self.crf(list_x,list_t)
return self.loss
def argmax(self,list_x):
~,path = self.crf.argmax(list_x)
return np.array(path,dtype="int32").flatten() #Puisque le chemin est un tableau de lots, il est transformé
En y repensant, il est presque inutile de créer une nouvelle classe ... Est-ce que ça va? Lors de l'envoi d'entrée au CRF, vous devez rassembler les variables dans un tableau (le document dit liste de variables). Lors de l'apprentissage, vous pouvez accélérer en les regroupant en lots. Dans mon cas, je l'ai écrit comme ci-dessous. Y est la sortie de DNN calculée à l'avance, et c'est un tableau de forme = (taille seq, 25) car tout est contenu dans un lot. T est la bonne série d'étiquettes.
DNN.py
#Une partie de la boucle d'apprentissage
startidx = np.random.randint(0,seqsize-256-1,size=16*100)#Déterminez au hasard le point de départ de la série
for i in range(0,32*100,32):
x_batch_list = [Variable(cp.asarray(Y[startidx[i:i+32]+j,:])) for j in range(256)]
t_batch_list = [Variable(cp.asarray(T[startidx[i:i+32]+j])) for j in range(256)]
opt.update(crfmodel,x_batch_list,t_batch_list) #cp est cupy
En bref, le flux consiste à prendre au hasard 32 séries de longueur 256 à chaque fois, à les combiner en un seul lot et à les donner au CRF. Dans la dernière version, CRF1d semble être capable de gérer des séries de différentes longueurs en batch, mais ici il est fixé à 256 longueurs. Facile à écrire. Il est possible de mettre DNN et CRF dans une chaîne et de les former ensemble, mais ici nous le divisons en deux étapes. Tout d'abord, utilisez les données d'entraînement pour entraîner uniquement le DNN. La fonction de perte est softmax_cross_entropy. Après cela, corrigez les paramètres DNN et entraînez le CRF. Au moment de l'estimation de l'étiquette, si vous donnez une série de sortie DNN, CRF1d.argmax () retournera l'itinéraire le plus probable dans la recherche de Viterbi. Benly.
Type d'étiquette
Allons-y avec la règle MajMin la plus simple. Ignorant Seventh, etc., en plus de 12 triades majeures et 12 triades mineures, il existe un total de 25 types, dont un label spécial appelé No Chord (silence, single tone, section percuss only, etc.).
Hyper paramètres
Les paramètres de DNN sont choisis de manière appropriée en se référant aux articles.
- Algorithme d'optimisation: AdaDelta --Nombre de dimensions d'entrée: 1008 (= 144x7) --Nombre de couches cachées: 4 --Nombre d'unités de couche cachées: 512
- Taux de chute: 0,5 L'optimisation CRF est également AdaDelta.
base de données
Les annotations de progression de code publiées par isophonics.net sont utilisées pour l'ensemble de données. Tous les albums des Beatles, les meilleurs albums de Queen et certains des albums de Kalore King, environ 200 chansons. La notation de l'annotation ressemble à ceci.
06_-_Let_It_Be.lab
0.000000 0.175157 N
0.175157 1.852358 C
1.852358 3.454535 G
3.434535 4.720022 A:min
...
...
Si le résultat de la reconnaissance par DNN est également sorti dans cette notation, le taux de réponse correct peut être calculé par mir_eval et le résultat de la reconnaissance peut être visualisé. L'ensemble de données est divisé au hasard en un ensemble de trains et un ensemble de test. Je ne fais pas de validation croisée car c'est gênant. Il n'y a pas de jeu de validation. Puisqu'il s'agit d'un problème de classification, le critère d'évaluation est le taux de réponse correct = (durée totale pendant laquelle l'étiquette estimée a répondu correctement) / (durée totale de la musique). Après avoir sorti le résultat de l'estimation dans le même format de texte que l'ensemble de données isophoniques, j'ai demandé à la bibliothèque mir_eval de calculer le taux de réponse correct.
Évaluation des performances
Nous avons mesuré la précision de classification de l'ensemble de test DNN formé et de l'ensemble de train, et la précision de reconnaissance finale en combinaison avec le CRF formé.
| DNN(train set) | DNN(test set) | DNN-CRF(train set) | DNN-CRF(test set) |
|---|---|---|---|
| 77.0% | 68.4% | 84.7% | 76.6% |
Vous pouvez voir que CRF contribue grandement à la précision de l'étiquetage des séries. Cela ressemble à ceci quand Audacity visualise le résultat de la reconnaissance. Ceci fait partie de la progression d'accords de Here Comes The Sun of the Beatles. Le bas est le résultat de la reconnaissance et le haut est la bonne réponse manuellement. Je ne peux pas attraper les petits changements dans le code, mais je peux voir que cela fonctionne principalement.

Essayez de résiduel
Remodelons DNN comme ResNet car c'est une bonne idée. La modification du style ResNet par Chainer est super facile. Par conséquent, Chainer est le plus fort.
DNN.py
class DNNRes(ChainList):
def __init__(self,links):
super(DNNRes,self).__init__(*links)
self.train = True
def __call__(self,x):
links = self.children()
li = links.next()
h = F.relu(li(x)) #Ne pas convertir de la couche d'entrée en Res
for i in xrange(self.__len__()-2):
li = links.next()
h = F.dropout(F.relu(li(h)),train=self.train)+h #ici+Ajoutez simplement h
y = links.next()(h)
return y
Il semble que le ResNet original ait deux couches cachées et un bloc résiduel, mais ~~ C'est ennuyeux ~~ Nous donnons la priorité à la compréhensibilité et rendons chaque couche résiduelle. Dans le cas de plusieurs couches, il est préférable de créer un bloc résiduel dans une classe distincte (chaîne). Le nombre de couches cachées est passé à 20. Comme la sur-conformité était terrible, j'ai ajouté une perte de poids légèrement plus forte en plus de Dropout. Facteur 0,001.
résultat!
| DNN(train set) | DNN(test set) | DNN-CRF(train set) | DNN-CRF(test set) |
|---|---|---|---|
| 78.8% | 74.0% | 85.5% | 80.5% |
La précision de l'ensemble de test s'est considérablement améliorée. Je suis allé à la barre des 80%.
Résultats du MIREX de cette année est à environ 86%, donc c'est encore loin, mais je suis assez bon dans ce domaine par rapport aux autres. (Je ne peux pas comparer exactement car ce n'est pas une validation croisée).
À propos de la mise en œuvre du CRF
Pour le CRF (à chaîne linéaire), voir Cet article et [Cet article (en anglais)](http://blog.echen.me/2012/01/ 03 / introduction-to-conditionitional-random-fields /) est recommandé. CRF est
P(Y|X)=\frac{\exp{E(X,Y)}}{\sum_{Y'}{\exp{E(X,Y)}}}
La probabilité conditionnelle de la série d'étiquettes Y est calculée comme ceci (la multiplication par -log donne une fonction de perte), mais il existe différentes définitions de la fonction d'élément E (X, Y). Dans le cas de Chainer (deviné d'après la documentation),
E(X,Y)=\sum_i{(x_{iy_i}+c_{y_{i-1}y_i})}
Et, ajoutez simplement la perte de classe de trame x (calculée par DNN, etc.) et le coût de transition d'étiquette c. Dans ce cas, le seul paramètre à apprendre est la matrice de coût de transition d'étiquette c.
Incorporer le DNN supérieur dans celui-ci (en supposant que X est une série spectrale),
E(X,Y)=\sum_i{(f_{dnn}(x_{iy_i})+c_{y_{i-1}y_i})}
On peut dire que c'était un grand CRF dans son ensemble en premier lieu. Au contraire, le coût de transition d'étiquette a également été rendu non linéaire.
E(X,Y)=\sum_i{(f_{dnn_1}(x_{iy_i})+f_{dnn_2}(c_{y_{i-1}y_i}))}
C'est peut-être une fourmi. J'ai l'impression que je m'approche progressivement de RNN. En regardant d'autres papiers,
E(X,Y)=\sum_i{(x_{iy_i}+c_{y_{i-1}y_i}+b_{y_i})}+\pi_{y_0}+\gamma_{y_N}
De cette façon, vous pouvez voir que le biais b est attaché et que le potentiel (caractéristique globale) au début et à la fin de la série d'étiquettes est incorporé. Est-ce possible avec un petit ajustement de l'implémentation de Chainer? En ce qui concerne les tâches de balisage de mots partiels, cela semble également être une fonction au cas par cas pour les suffixes (tels que -ly). De cette façon, il est souvent utilisé dans la même tâche qu'il s'agit d'un modèle discriminant (la probabilité conditionnelle est calculée directement), la fonction d'élément est flexible (des fonctionnalités globales et des règles heuristiques peuvent être incorporées), et il n'y a aucune restriction sur les valeurs des paramètres. Différence avec le HMM. Surtout, si les paramètres peuvent être différenciés, il peut être appris par descente de gradient, donc il est compatible avec NN! le plus fort! Par conséquent, il semble que l'application se développe dans la tâche d'étiquetage des séries. On s'attend également à ce que Chainer ait plus de variations à l'avenir.
- Supplément: j'ai tracé la matrice c dans cet exemple.
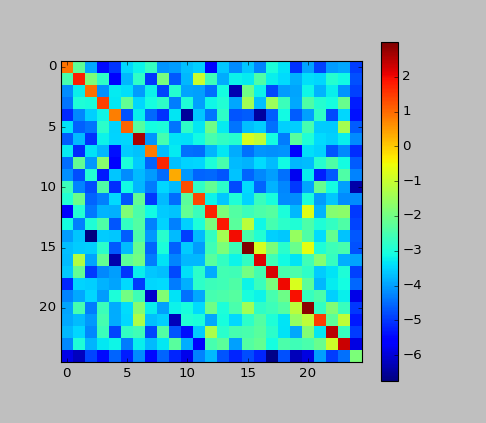 A partir de la valeur élevée de la ligne diagonale principale, nous pouvons voir que le CRF "travaille dans le sens de la suppression du changement d'étiquette". C'était presque comme ça dans HMM.
A partir de la valeur élevée de la ligne diagonale principale, nous pouvons voir que le CRF "travaille dans le sens de la suppression du changement d'étiquette". C'était presque comme ça dans HMM.
Résumé
Veuillez me pardonner car le code source complet ne peut être montré à personne. Je suis un étudiant de recherche sur le sujet de la copie automatique de l'oreille, j'ai donc présenté ce que j'ai appris dans une certaine mesure (également en tant que missionnaire dans le domaine MIR). Formellement, c'est un modèle très simple pour l'étiquetage des séries, mais il semble toujours fonctionner assez bien dans la tâche de reconnaissance de la progression du code. Si vous en avez envie, vous pouvez approfondir DNN, le rendre CNN ou même le rendre RNN. Je fais actuellement un modèle un peu plus compliqué, mais j'écris un article, donc j'espère pouvoir le présenter à nouveau. J'utilise Chainer depuis longtemps, mais c'est vraiment bien. Le sentiment de pouvoir assembler comme vous l'aviez imaginé est super confortable et utile. Donc le plus fort (deuxième fois).
Supplément: j'ai oublié de normaliser
J'ai complètement oublié de normaliser l'entrée dans le pré-traitement. Quel bordel. Recommencer. Mettez la normalisation entre les étapes 3 (conversion du journal) et 4 du prétraitement. Je pense qu'il y a plusieurs façons de le faire, mais ici je vais le faire avec la normalisation de la variance moyenne globale (trouver la moyenne et la var du spectrogramme entier pour une chanson).
norm(X)=\frac{X-mean(X)}{var(X)}
Converti en une forme qui satisfait NN, avec une valeur moyenne de 0 et une variance de 1.
J'ai également examiné la soi-disant compression logarithmique à l'étape 3. À l'origine, ce processus était un pré-processus pour compresser le bruit de la quantité de fonction appelée Chromagram, qui est souvent utilisée dans la même tâche, mais comme Chromagram est non négatif, il était nécessaire de conserver la propriété de +1 lors de la conversion logarithmique. Dans un autre article sur l'apprentissage en profondeur, je l'ai utilisé pour le prétraitement du spectrogramme et je l'ai imité, mais quand j'y pense, il n'est pas nécessaire de limiter la plage de valeurs d'entrée à non négative, donc si c'est le cas, +1 pour compresser la plage de valeurs C'est un gaspillage de le faire. Vous n'avez donc pas besoin de +1.
f(X)=log(0.01+X)
Si vous écrivez normalement le journal, c'est OK. 0.01 est pour éviter les valeurs nulles. J'ai essayé à nouveau avec les paramètres DNN-CRF résiduels.
| DNN(train set) | DNN(test set) | DNN-CRF(train set) | DNN-CRF(test set) |
|---|---|---|---|
| 84.8% | 77.4% | 88.6% | 82.0% |
Il a beaucoup grandi. Après tout, le prétraitement est important. La normalisation est importante. Soyons tous prudents!
Recommended Posts