Il existe différents noms tels que filtre à particules / filtre à particules et Monte Carlo séquentiel (SMC), mais dans cet article, nous utiliserons le nom de filtre à particules. Je voudrais essayer d'implémenter ce filtre de particules en Python pour estimer les variables latentes du modèle d'espace d'états.

Le modèle d'espace d'états est divisé en plusieurs modèles, mais cette fois, nous traiterons du modèle local (modèle de tendance de différence du 1er étage), qui est un modèle simple. Si vous voulez savoir ce qu'il y a d'autre dans ce type de tendance de modèle d'espace d'états, cliquez ici (http://www.statsmodels.org/stable/generated/statsmodels.tsa.statespace.structural.UnobservedComponents.html# Veuillez vous référer à statsmodels.tsa.statespace.structural.UnobservedComponents).

\begin{aligned}
x_t &= x_{t-1} + v_t, \quad v_t \sim N(0, \alpha^2\sigma^2)\quad &\cdots\ {\rm System\ model} \\
y_t &= x_{t} + w_t, \quad w_t \sim N(0, \sigma^2)\quad &\cdots\ {\rm Observation\ model}
\end{aligned}

$ x_t $ représente l'état latent au temps t et $ y_t $ représente la valeur observée.

Pour les données à utiliser, utilisez les exemples de données (http://daweb.ism.ac.jp/yosoku/) de "Bases de la modélisation statistique utilisée pour la prédiction".

Ces données de test peuvent être obtenues à partir d'ici (http://daweb.ism.ac.jp/yosoku/).

À l'aide du filtre à particules, vous pouvez estimer l'état latent à chaque instant à l'aide de particules, c'est-à-dire de nombres aléatoires, comme indiqué dans le graphique ci-dessous. Les particules rouges sont des particules, et vous pouvez effectuer un filtrage en attribuant des poids basés sur la probabilité à ces particules et en prenant une moyenne pondérée, et vous pouvez estimer l'état latent comme indiqué par la ligne verte. Je vais. Comme le montre le modèle d'observation (modèle d'observation), la valeur d'observation bleue (données actuellement obtenues) a un bruit qui suit une distribution normale à partir de cet état latent, et [valeur de l'état latent] + [ Le modèle suppose que [bruit] = [valeur observée en tant que valeur réalisée].

Ce qui suit décrit un algorithme qui estime la valeur de l'état latent en filtrant avec ce filtre à particules.

Cliquez ici pour l'animation de flux.

1. Code Python

La classe principale ParticleFilter est ci-dessous. Le code complet est ici [https://github.com/matsuken92/Qiita_Contents/blob/master/particle_filter/particle_filter_class.ipynb)

class ParticleFilter(object):
    def __init__(self, y, n_particle, sigma_2, alpha_2):
        self.y = y
        self.n_particle = n_particle
        self.sigma_2 = sigma_2
        self.alpha_2 = alpha_2
        self.log_likelihood = -np.inf
    
    def norm_likelihood(self, y, x, s2):
        return (np.sqrt(2*np.pi*s2))**(-1) * np.exp(-(y-x)**2/(2*s2))

    def F_inv(self, w_cumsum, idx, u):
            if np.any(w_cumsum < u) == False:
                return 0
            k = np.max(idx[w_cumsum < u])
            return k+1
        
    def resampling(self, weights):
        w_cumsum = np.cumsum(weights)
        idx = np.asanyarray(range(self.n_particle))
        k_list = np.zeros(self.n_particle, dtype=np.int32) #Répertorier l'emplacement de stockage des k échantillonnés
        
        #Obtenez des indices pour rééchantillonner en fonction du poids de la distribution uniforme
        for i, u in enumerate(rd.uniform(0, 1, size=self.n_particle)):
            k = self.F_inv(w_cumsum, idx, u)
            k_list[i] = k
        return k_list

    def resampling2(self, weights):
        """
Échantillonnage stratifié avec moins de calculs
        """
        idx = np.asanyarray(range(self.n_particle))
        u0 = rd.uniform(0, 1/self.n_particle)
        u = [1/self.n_particle*i + u0 for i in range(self.n_particle)]
        w_cumsum = np.cumsum(weights)
        k = np.asanyarray([self.F_inv(w_cumsum, idx, val) for val in u])
        return k
    
    def simulate(self, seed=71):
        rd.seed(seed)

        #Nombre de données de séries chronologiques
        T = len(self.y)
        
        #Variable latente
        x = np.zeros((T+1, self.n_particle))
        x_resampled = np.zeros((T+1, self.n_particle))
        
        #Valeur initiale de la variable latente
        initial_x = rd.normal(0, 1, size=self.n_particle)   #--- (1)
        x_resampled[0] = initial_x
        x[0] = initial_x

        #poids
        w        = np.zeros((T, self.n_particle))
        w_normed = np.zeros((T, self.n_particle))

        l = np.zeros(T) #Responsabilité dans le temps

        for t in range(T):
            print("\r calculating... t={}".format(t), end="")
            for i in range(self.n_particle):
                #Appliquer la tendance différentielle du 1er étage
                v = rd.normal(0, np.sqrt(self.alpha_2*self.sigma_2)) # System Noise　#--- (2)
                x[t+1, i] = x_resampled[t, i] + v #Ajout du bruit du système
                w[t, i] = self.norm_likelihood(self.y[t], x[t+1, i], self.sigma_2) # y[t]Responsabilité de chaque particule vis-à-vis de
            w_normed[t] = w[t]/np.sum(w[t]) #Standardisation
            l[t] = np.log(np.sum(w[t])) #Chaque fois, enregistrez la probabilité

            # Resampling
            #k = self.resampling(w_normed[t]) #Indice de particules obtenu par ré-échantillonnage
            k = self.resampling2(w_normed[t]) #Indice des particules acquises par ré-échantillonnage (échantillonnage en couches)
            x_resampled[t+1] = x[t+1, k]
            
        #Probabilité logarithmique globale
        self.log_likelihood = np.sum(l) - T*np.log(n_particle)
        
        self.x = x
        self.x_resampled = x_resampled
        self.w = w
        self.w_normed = w_normed
        self.l = l
        
    def get_filtered_value(self):
        """
Calculez la valeur en filtrant par la valeur moyenne pondérée par le poids de la vraisemblance
        """
        return np.diag(np.dot(self.w_normed, self.x[1:].T))
        
    def draw_graph(self):
        #Dessin graphique
        T = len(self.y)
        
        plt.figure(figsize=(16,8))
        plt.plot(range(T), self.y)
        plt.plot(self.get_filtered_value(), "g")
        
        for t in range(T):
            plt.scatter(np.ones(self.n_particle)*t, self.x[t], color="r", s=2, alpha=0.1)
        
        plt.title("sigma^2={0}, alpha^2={1}, log likelihood={2:.3f}".format(self.sigma_2, 
                                                                                 self.alpha_2, 
                                                                                 self.log_likelihood))
        plt.show()

2. Fonctionnement du filtre à particules

Je republierai l'animation du flux de processus.

Ci-dessous, je vais vous expliquer une image à la fois.

STEP1: Il commence à partir du point t-1, mais si t = 1, la valeur initiale est requise. Ici, nous allons générer un nombre aléatoire qui suit $ N (0, 1) $ comme valeur initiale et l'utiliser comme valeur initiale. Si t> 1, le résultat du temps précédent correspond à ce $ X_ {re, t-1 | t-1} $. スライド01.png

Voici le code de la partie initialisation de la particule.

initial_x = rd.normal(0, 1, size=self.n_particle)   #--- (1)

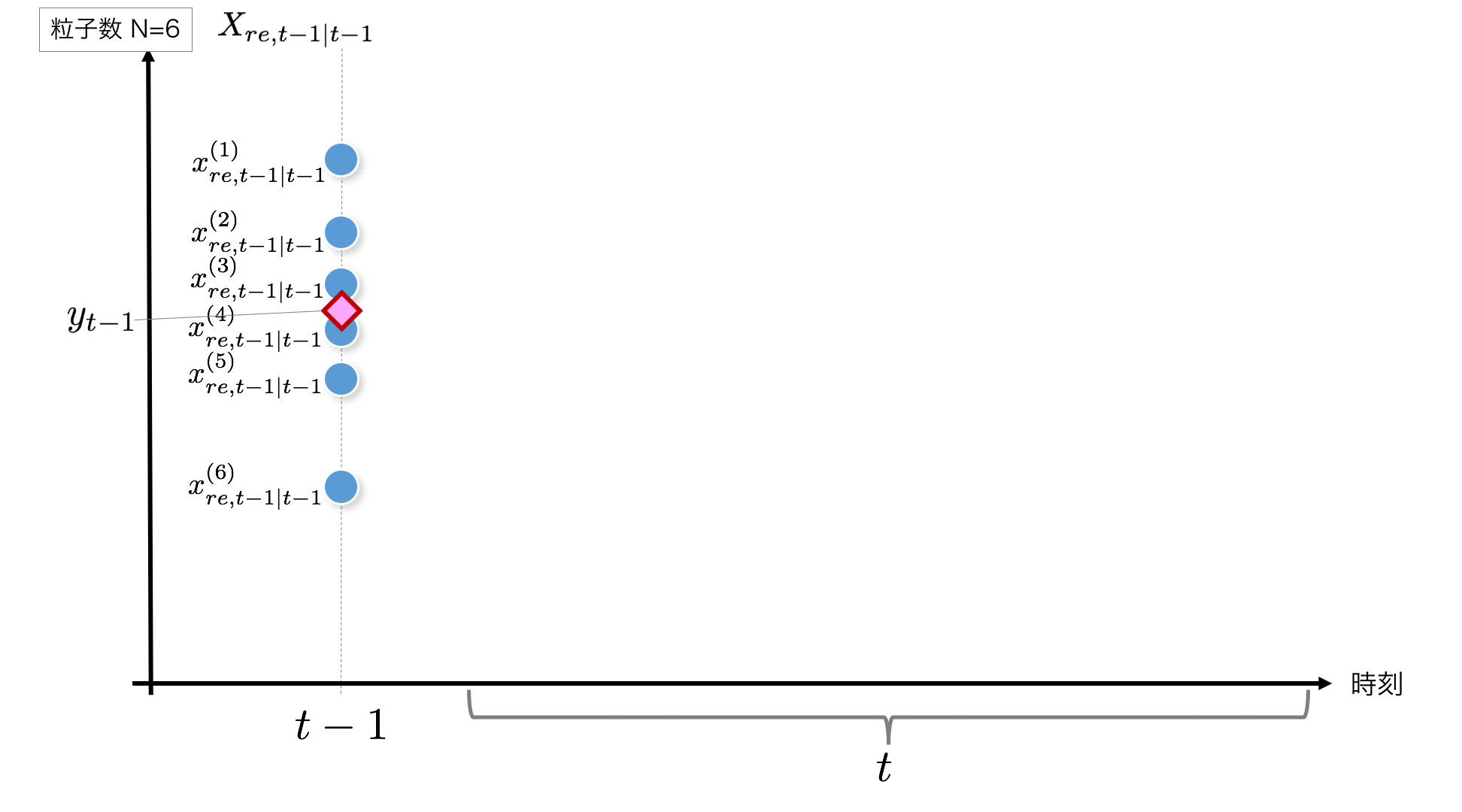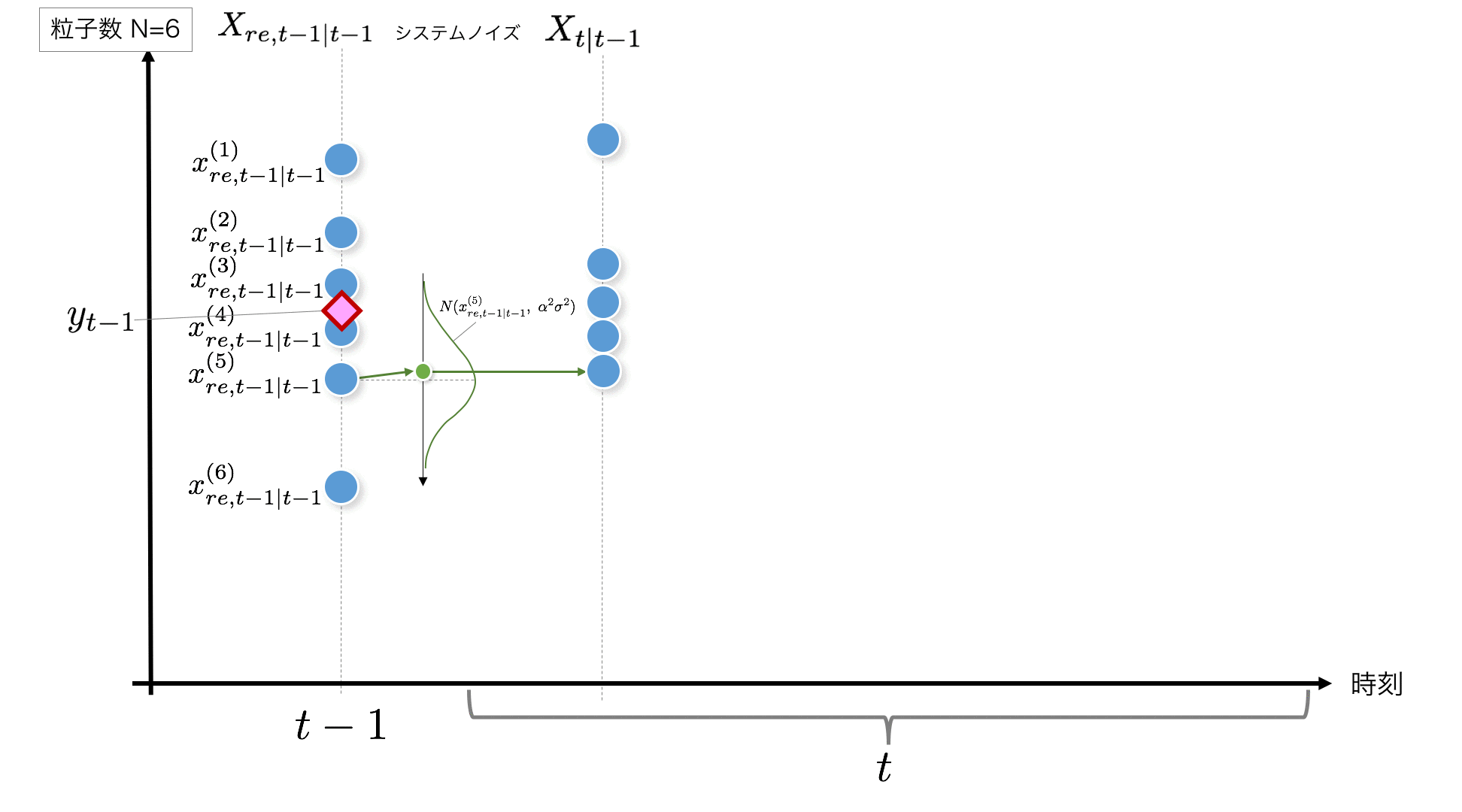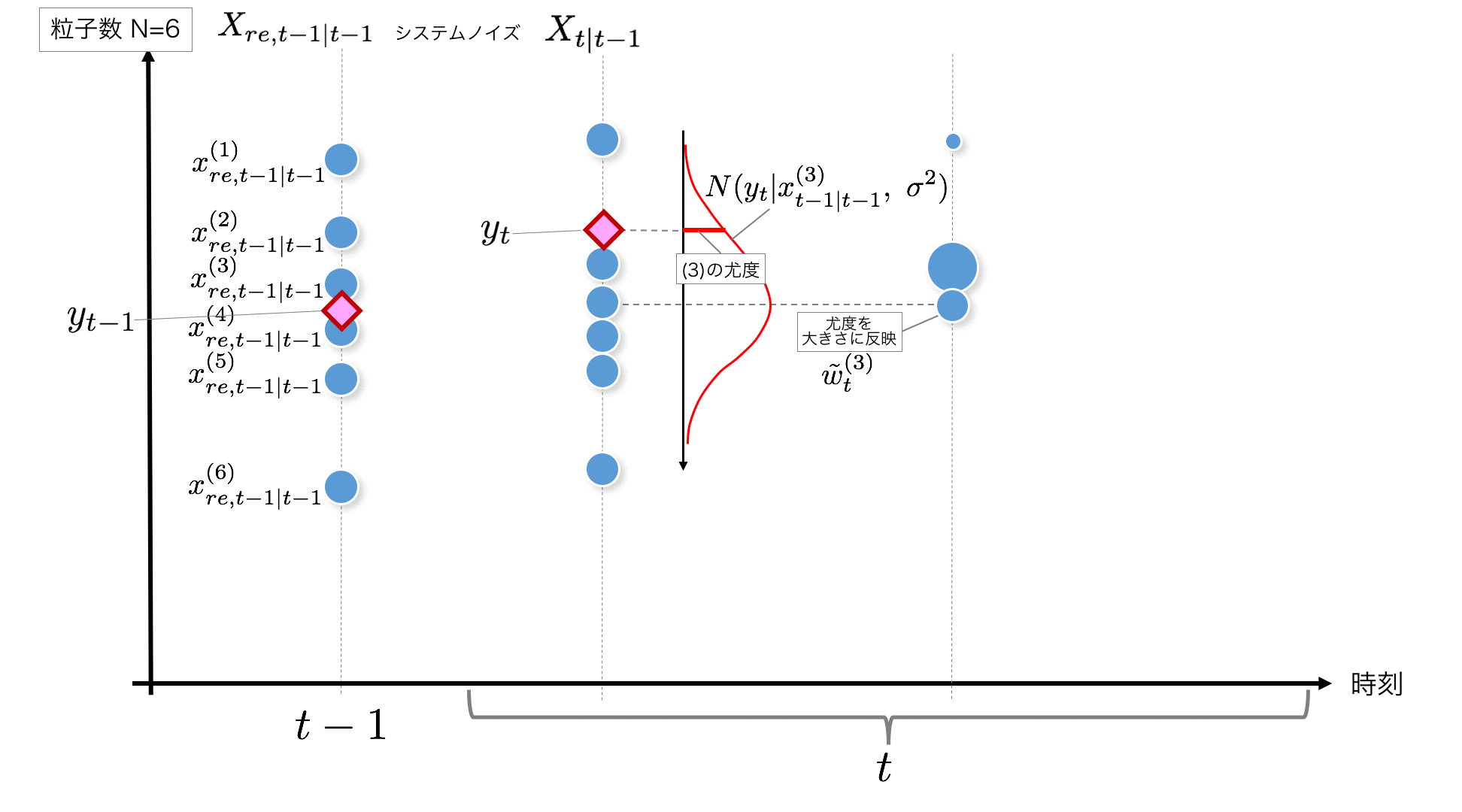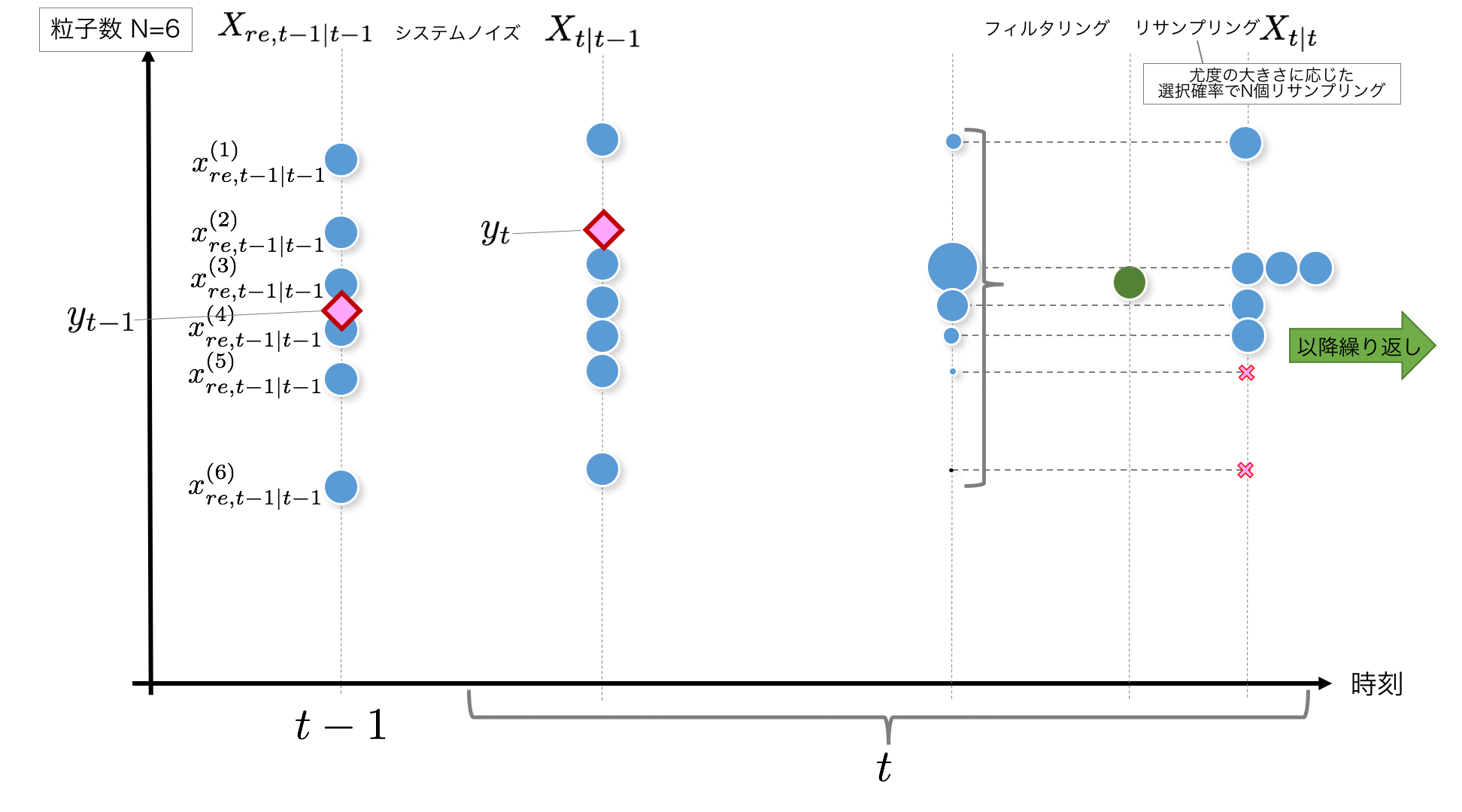
STEP2: Selon le modèle du système, le bruit sera ajouté lors du passage de $ t-1 $ à l'heure actuelle à $ t $ la prochaine fois. Ici, on suppose que la distribution normale $ N (0, \ alpha ^ 2 \ sigma ^ 2) $ est suivie. Faites ceci pour le nombre de particules.

x_t = x_{t-1} + v_t, \quad v_t \sim N(0, \alpha^2\sigma^2)\quad \cdots\ {\rm System\ model}

Le code ajoute du bruit selon $ N (0, \ alpha ^ 2 \ sigma ^ 2) $ à chaque particule comme indiqué ci-dessous.

v = rd.normal(0, np.sqrt(self.alpha_2*self.sigma_2)) # System Noise　#--- (2)
x[t+1, i] = x_resampled[t, i] + v #Ajout du bruit du système

STEP3: Après toutes les valeurs de particules $ x_ {t | t-1} $ après l'ajout du bruit, $ y_t $, qui est la valeur observée au temps $ t $, est obtenue, donc la probabilité de chaque particule est calculée. Faire. La vraisemblance calculée ici est la plus probable de la particule à la valeur observée $ y_t $ qui vient d'être obtenue. Je veux l'utiliser comme poids de la particule, donc je la mets dans une variable et la sauvegarde. Ce calcul de vraisemblance est également effectué pour le nombre de particules.

La probabilité est

p(y_t|x_{t|t-1}^{(i)}) = w_{t}^{(i)} = {1 \over \sqrt{2\pi\sigma^2}} \exp \left\{
-{1 \over 2} {(y_t - x_{t|t-1}^{(i)})^2 \over \sigma^2}
\right\}

Calculez avec. Après avoir calculé la probabilité pour toutes les particules, les poids normalisés (pour additionner jusqu'à 1)

\tilde{w}^{(i)}_t = { w^{(i)}_t \over \sum_{i=1}^N w^{(i)}_t}

Préparez-vous également.

def norm_likelihood(self, y, x, s2):
    return (np.sqrt(2*np.pi*s2))**(-1) * np.exp(-(y-x)**2/(2*s2))

w[t, i] = self.norm_likelihood(self.y[t], x[t+1, i], self.sigma_2) # y[t]Responsabilité de chaque particule vis-à-vis de
w_normed[t] = w[t]/np.sum(w[t]) #Standardisation

STEP4: Moyenne pondérée en utilisant le poids $ \ tilde {w} ^ {(i)} _t $ enregistré précédemment

\sum_{i=1}^N \tilde{w}^{(i)}_t x_{t|t-1}^{(i)}

Est calculé comme étant la valeur filtrée $ x $.

Dans le code, le suivant get_filtered_value () est applicable.

def get_filtered_value(self):
    """
Calculez la valeur en filtrant par la valeur moyenne pondérée par le poids de la vraisemblance
    """
    return np.diag(np.dot(self.w_normed, self.x[1:].T))

STEP5: Considérant le poids $ \ tilde {w} ^ {(i)} _t $ basé sur la vraisemblance comme probabilité d'être extrait,

X_{t|t-1}=\{x_{t|t-1}^{(i)}\}_{i=1}^N

Rééchantillonner N pièces de. C'est ce qu'on appelle le rééchantillonnage, mais c'est une image d'une opération dans laquelle les particules à faible probabilité sont éliminées et les particules à forte probabilité sont divisées en plusieurs morceaux.

k = self.resampling2(w_normed[t]) #Indice des particules acquises par rééchantillonnage (échantillonnage en couches)
x_resampled[t+1] = x[t+1, k]

Lors du rééchantillonnage, créez une fonction de distribution empirique à partir de $ \ tilde {w} ^ {(i)} _t $ comme indiqué ci-dessous, et créez la fonction inverse pour rendre la plage de (0,1] uniforme. Chaque particule peut être extraite d'un nombre aléatoire avec une probabilité en fonction du poids.

F_inv () est le code qui traite la fonction inverse, et resampling2 () est le code qui effectue un échantillonnage en couches. L'échantillonnage stratifié est mis en œuvre en référence à "Kalman Filter-Time Series Prediction and State Space Model Using R- (Statistics One Point 2)".

\begin{aligned}
u &\sim U(0, 1) \\
k_i &= F^{-1}((i-1+u)/N) \quad i=1,2,\cdots, N \\
x^{(i)}_{t|t} &= x^{(k_i)}_{t|t-1}
\end{aligned}

C'est comme ça. Au lieu de générer N nombres aléatoires uniformes entre (0, 1], générez un seul nombre aléatoire uniforme entre (0, 1 / N] et 1 / N entre (0, 1] On suppose que N pièces sont échantillonnées avec une largeur égale en les décalant une par une.

def F_inv(self, w_cumsum, idx, u):
        if np.any(w_cumsum < u) == False:
            return 0
        k = np.max(idx[w_cumsum < u])
        return k+1

def resampling2(self, weights):
    """
Échantillonnage stratifié avec moins de calculs
    """
    idx = np.asanyarray(range(self.n_particle))
    u0 = rd.uniform(0, 1/self.n_particle)
    u = [1/self.n_particle*i + u0 for i in range(self.n_particle)]
    w_cumsum = np.cumsum(weights)
    k = np.asanyarray([self.F_inv(w_cumsum, idx, val) for val in u])
    return k

En effectuant cette opération de t = 1 à T, des particules peuvent être générées et filtrées.

Le résultat est le graphique ci-dessous.

3. Vérifiez que l'implémentation est correcte en la comparant aux résultats du filtre Kalman

Maintenant, je veux vérifier si le filtre de particules implémenté se comporte correctement ou s'il produit le même résultat en le comparant avec le résultat du filtre de Kalman dans Stats Models au cas où. je pense

# Unobserved Components Modeling (via Kalman Filter)Exécution de
import statsmodels.api as sm

# Fit a local level model
mod_ll = sm.tsa.UnobservedComponents(df.data.values, 'local level')
res_ll = mod_ll.fit()

print(res_ll.summary())

# Show a plot of the estimated level and trend component series
fig_ll = res_ll.plot_components(legend_loc="upper left", figsize=(12,8))
plt.tight_layout()

Si vous superposez cela avec le résultat du filtre à particules, c'est presque exactement la même chose! : en riant:

Il s'agit de la mise en œuvre du filtre à particules. L'explication de pourquoi cela fonctionne est une lecture incontournable car Tomoyuki Higuchi (Auteur), les bases de la modélisation statistique utilisée pour la prédiction, est très facile à comprendre.

devoirs

Ajout d'un intervalle de confiance à chaque instant
Prévision après T
Je n'ai pas encore ajouté de lissage de patte fixe, je veux donc l'ajouter.
La recherche d'hyper paramètres n'est pas bonne avec Grid Search, je veux donc y réfléchir.
Prend en charge les tendances autres que les modèles locaux et l'ajout de conditions saisonnières
Accélérant

référence

Code utilisé sur cette page https://github.com/matsuken92/Qiita_Contents/blob/master/particle_filter/particle_filter_class.ipynb
Bases de la modélisation statistique utilisée pour la prédiction Tomoyuki Higuchi (Auteur) https://www.amazon.co.jp/dp/4061557955
Prédiction de séries chronologiques par filtre de Kalman et modèle d'espace d'état utilisant R- (Statistics One Point 2) https://www.amazon.co.jp/dp/4320112539
Statistiques computationnelles 2 Méthode de Monte Carlo en chaîne de Markov et ses environs (Frontier of Statistical Science 12) Yukito Iba (Auteur), Masami Tanemura (Auteur) https://www.amazon.co.jp/dp/4000068520
StatsModels: Unobserved Components Modeling
http://www.statsmodels.org/stable/generated/statsmodels.tsa.statespace.structural.UnobservedComponents.html#statsmodels.tsa.statespace.structural.UnobservedComponents

Implémentation du filtre à particules par Python et application au modèle d'espace d'états

1. Code Python

2. Fonctionnement du filtre à particules

3. Vérifiez que l'implémentation est correcte en la comparant aux résultats du filtre Kalman

devoirs

référence