Pendule inversé avec contrôle prédictif du modèle

J'ai essayé le contrôle de prédiction de modèle en utilisant cvxpy, qui est l'un des modules d'optimisation de Python. Comme sujet, j'ai choisi un pendule inversé, ce qui n'est pas exagéré de dire que c'est un système de contrôle Hello, World!

Contrôle prédictif du modèle et pendule inversé

Fondamentalement, l'exemple de code sur le site suivant est le principal.

Contrôle de prédiction de modèle et exemple de code

À propos, le pendule inversé manipulé cette fois est le [Pendule inversé] de Wikipedia (https://ja.wikipedia.org/wiki/%E5%80%92%E7%AB%8B%E6%8C%AF%E5%AD%90 ) Est supposé être un pendule inversé entraîné par un chariot. L'équation du mouvement est la suivante. Chaque variable est fondamentalement unifiée avec l'article de Wikipedia, mais seuls F et u sont différents.

(M + m)\ddot{x} - ml\ddot{\theta}cos\theta + ml\dot{\theta}^2sin\theta = u \\
l\ddot{\theta} - gsin\theta = \ddot{x}cos\theta

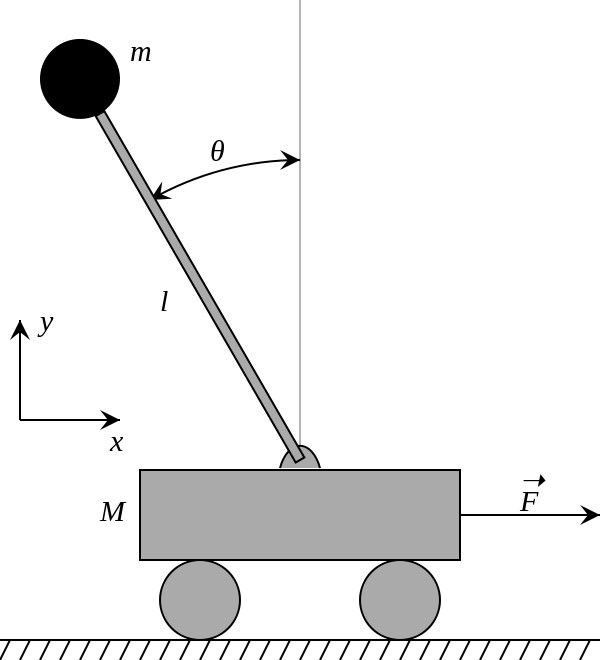
En partant de l'hypothèse que θ est proche de 0, nous faisons une approximation et exprimons le modèle sous forme d'équation linéaire.

\frac{d}{dt}
\begin{pmatrix}
x \\
\dot{x} \\
\theta \\
\dot{\theta}
\end{pmatrix}
=
\begin{pmatrix}
0 & 1 & 0 & 0 \\
0 & 0 & \frac{mg}{M} & 0 \\
0 & 0 & 0 & 1 \\
0 & 0 & \frac{(M + m)g}{lM} & 0
\end{pmatrix}
\begin{pmatrix}
x \\
\dot{x} \\
\theta \\
\dot{\theta}
\end{pmatrix}
+
\begin{pmatrix}
0 \\
\frac{1}{M} \\
0 \\
\frac{1}{lM}
\end{pmatrix}
u

A = 
\begin{pmatrix}
0 & 1 & 0 & 0 \\
0 & 0 & \frac{mg}{M} & 0 \\
0 & 0 & 0 & 1 \\
0 & 0 & \frac{(M + m)g}{lM} & 0
\end{pmatrix}
Δt
+
\begin{pmatrix}
1 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 \\
0 & 0 & 1 & 0 \\
0 & 0 & 0 & 1
\end{pmatrix} \\
B =
\begin{pmatrix}
0 \\
\frac{1}{M} \\
0 \\
\frac{1}{lM}
\end{pmatrix}
Δt

{\bf x}_{t+1} = A{\bf x}_{t} + Bu

Δt est le cycle de contrôle. Si Δt est de 0,1 [s], l'entrée de commande est modifiée toutes les 0,1 secondes en fonction de l'état actuel.

code

Définissez l'équation linéaire comme suit:

mpc.py

import time
from cvxpy import *
import numpy as np
import matplotlib.pyplot as plt

n_state = 4   #Nombre d'états
m_state = 1   #Nombre d'entrées de commande
T = 100  #Décidez du nombre d'étapes à prévoir

#simulation parameter
delta_t = 0.01

M = 1.0  # [kg]
m = 0.3  # [kg]
g = 9.8  # [m/s^2]
l = 0.6  # [m]

# Model Parameter
A = np.array([
	[0.0, 1.0, 0.0, 0.0],
	[0.0, 0.0, m * g / M, 0.0],
	[0.0, 0.0, 0.0, 1.0],
	[0.0, 0.0, g * (M + m) / (l * M), 0.0]
	])
A = np.eye(n_state) + delta_t * A

B = np.array([
	[0.0],
	[1.0 / M],
	[0.0],
	[1.0 / (l * M)]
	])
B = delta_t * B

#État initial du pendule inversé
#Cette fois, nous visons à ce que tout converge vers 0
x_0 = np.array([
	[-0.02],
	[0.0],
	[0.02],
	[0.0]
	])

x = Variable(n_state, T+1)
u = Variable(m_state, T)

Le code ci-dessous définit en fait la fonction de coût et effectue l'optimisation. Utilisez cost_arr pour ajuster le poids de chaque état. Le code ici est presque simplement copié à partir de Model Predictive Control and Sample Code.

mpc.py

cost_arr = np.array([
	[1.0, 0.0, 0.0, 0.0],
	[0.0, 1.0, 0.0, 0.0],
	[0.0, 0.0, 0.1, 0.0],
	[0.0, 0.0, 0.0, 0.1]
	])

states = []
for t in range(T):
    #Trouvez le tableau u tel que la valeur de la fonction de coût soit petite
    cost = sum_squares(cost_arr*x[:,t+1]) + sum_squares(0.1*u[:,t])
    #Donner des équations de contraintes (équations linéaires et limites d'entrée de contrôle)
    constr = [x[:,t+1] == A*x[:,t] + B*u[:,t],
    			norm(u[:,t], 'inf') <= 20.0]
    states.append( Problem(Minimize(cost), constr) )
# sums problem objectives and concatenates constraints.
prob = sum(states)
#Ajouter deux contraintes supplémentaires
#Dernier état(État après l'étape T)Est tout 0, c'est-à-dire l'état idéal
#Et puisque l'état actuel x0 est un fait, il devient une contrainte
prob.constraints += [x[:,T] == 0, x[:,0] == x_0]

start = time.time()
result=prob.solve(verbose=True)
elapsed_time = time.time() - start
print("calc time:{0} [sec]".format(elapsed_time))

#S'il diverge, il finit comme hors de contrôle
if result == float("inf"):
    print("Cannot optimize")
    import sys
    sys.exit()

À propos, le code ci-dessus équivaut à un contrôle. Etant donné que le contrôle est toujours effectué, le pendule inversé peut être maintenu dans un état debout sans tomber en répétant le processus ci-dessus.

Le code du contrôle prédictif du modèle itératif est le suivant.

mpc.py

cnt = 0
#Contrôle 1000 fois
while cnt < 1000:
    states = []
    for t in range(T):
        cost = sum_squares(cost_arr*x[:,t+1]) + sum_squares(0.1*u[:,t])
        constr = [x[:,t+1] == A*x[:,t] + B*u[:,t],
                    norm(u[:,t], 'inf') <= 20.0]
        states.append( Problem(Minimize(cost), constr) )
    # sums problem objectives and concatenates constraints.
    prob = sum(states)
    prob.constraints += [x[:,T] == 0, x[:,0] == x_0]

    start = time.time()
    result=prob.solve(verbose=False)
    elapsed_time = time.time() - start

    if result == float("inf"):
        print("Cannot optimize")
        import sys
        sys.exit()

    #Obtenez la gamme optimale d'entrées de contrôle
    good_u_arr = np.array(u[0,:].value[0,:])[0]
    
    #Entrez l'entrée de contrôle et obtenez l'état suivant
    #Je ne pense pas au bruit cette fois
    x_next = np.dot(A, x_0) + B * good_u_arr[0]
    x_0 = x_next

    cnt += 1

    #De gauche à droite x(Position du chariot), \dot{x}(La vitesse du chariot), rad(Angle du pendule), \dot{rad}(Vitesse angulaire du pendule)
    print(x_next.reshape(-1))

Il est souvent hors de contrôle en fonction de l'état initial du pendule inversé.

Alors que le contrôle prédictif du modèle a des performances de contrôle élevées, il semble avoir le problème d'une grande quantité de calcul. Mon PC s'est également considérablement réchauffé.