Predict time series data with neural network
When dealing with time series data in a neural network, use a recurrent neural network. This time, I will explain about the recurrent neural network.
(Because it is long, the neural network is abbreviated as NN, and the recurrent neural network is abbreviated as RNN)
Overview of RNN
In some data, the previous data has a correlation with the next data, such as when an "x" appears, there is a high possibility that an "y" will come. Specifically, it is words and music (such as "ha" or "ga" often comes after "I"). For such time-series correlated data, it is naturally tempting to consider previously generated data. Is it possible to input previously generated data to NN? The answer is RNN.
Specifically, it is as shown in the figure below.

The contents of the hidden layer at time $ t $ are treated as input at the next time $ t + 1 $. The hidden layer of $ t + 1 $ continues with $ t + 2 $, but the point is that the previous hidden layer is also used for learning the next hidden layer.
RNN type
| name | Combined target | Feature |
|---|---|---|
| Fully recurrent network | All nodes(1:N) | Combine completely bidirectionally including itself |
| Hopfield network | All nodes(1:N-1) | Bidirectional join, does not include itself in the join target |
| Elman network | 1:1 (Hidden layer->Hidden layer) | Input layer / context(Hidden layer)・ Three-layer structure of output layer |
| Jordan network | 1:1 (Output layer->Hidden layer) | Input layer / context(Hidden layer)・Output layerの3層構造 |
| Echo state network (ESN) | 1->1? | The target of joining is a set of nodes(reservoir)Randomly determined from |
| Long short term memory network (LSTM) | - | Instead of an RNN node, a Block that can hold input values is adopted. High precision |
| Bi-directional RNN (BRNN) | - | Bidirectional(past->future/future->past)A combination of RNNs |
Hopfield network has applicable to optimization problems in addition to general classification. /~kanakubo/research/neuro/hopfieldnetwork.html) This is a model.
Elman / Jordan is the simplest form as it is called Simple recurrent networks. If you want to use RNN, you should try either one first, and if there is an accuracy problem, try switching to another method. The difference between Elman / Jordan is as above (whether the previous data is reflected from the hidden layer or the output layer), but here It is also written in detail in. There is no exact superiority or inferiority, but I think Elman is more flexible because the amount of propagation next can be changed depending on the number of hidden layers.
Echo state network is a model with a different coat color, and it is stored in a pool called Reservoir (meaning a reservoir etc.) without connecting nodes in advance. The style is to randomly / dynamically join after the input is given. The point is that there is no predetermined connection in the human brain, so it was created with the concept of imitating it and connecting fluidly. It seems that this is also called Liquid State Machines (literally, liquid mechanism).
Long short term memory network (LSTM) and Bi-directional RNN (BRNN) have no particular restrictions on how to join. LSTMs use LSTM blocks to remember weights instead of simple nodes. This is to solve the learning challenges in RNNs and will be explained later.
Bi-directional RNNs can improve accuracy by learning not only one-way learning from the past to the future, but also time series in a certain negative direction from the future to the past.
Learning RNN
The following documents are very carefully written about learning RNNs. Although it is in English, there is almost no Japanese literature on RNN at this stage (2015/1), so there is no choice but to give up and read it.
Learning RNNs is generally very slow to converge. You need to lower the learning rate for accuracy, but lowering it will slow down the already slow convergence. This is a trade-off, but there seems to be a way to solve the gradient instability in the optimization process (see [EFFICIENT SECOND-ORDER LEARNING ALGORITHMS FOR DISCRETE-TIME RECURRENT NEURAL NETWORKS] for details]. (See http://ir.nmu.org.ua/bitstream/handle/123456789/120274/866d31771b48ba40c56fcc039f091b9b.pdf?sequence=1&isAllowed=y#page=58).
One thing I can say is that, at the moment (2015/1), there is no established method that has no problem in accuracy and speed in RNN learning, so naturally there is no library that implements it. .. It is necessary to practice here steadily.
BPTT (BackPropagation Through Time) The basic idea is that backpropagation should be applicable as usual, as RNNs can be considered long NNs when expanded. The image is as follows.

The error propagates from the last time T to the first 0. Therefore, the error of the output layer at a certain time t is the sum of "the difference between the teacher (teacher data) and output (output) at time t" and "the error propagated from t + 1".
As is clear from the figure, BPTT cannot train without the data up to the last T, that is, all the time series data. Therefore, it is necessary to take measures such as cutting out only the latest data for long data.
This BPTT has various problems, and various learning methods have been devised to deal with them.
LSTM(Long short term memory) If T is too large, that is, for long time series data, the error from the upper layer may be diminished or conversely very large due to a calculation problem (this is detailed here (p8 ~)]( http://www.slideshare.net/beam2d/pfi-seminar-20141030rnn)). The larger the value, the greater the limit of the maximum value, but since it can't be helped to disappear, the idea of LSTM is to propagate the error so that it is not attenuated.
teacher forcing In RNN, the output of t becomes the input of t + 1, and so on, but at the time of learning, the correct answer of the input to t + 1 is clear from the teacher, so the method of using it as it is is. This allows each layer to learn by ignoring the influence from the lower layer and increase the convergence speed, but it seems that the output is not stable when actually executed (after learning).
RPROP(Resilient backpropagation) This is the method also used for regular NNs. When training NN, the gradient is calculated, and the weight ($ \ eta $) is multiplied according to how the direction (sign) of the gradient changed between the previous time and now (see [here](http for details). You can read more about: //paginas.fe.up.pt/~ee02162/dissertacao/RPROP%20paper.pdf).
- If the sign is the same between the previous time and this time, the learning is accelerated by weighting the gradient.
- If the sign is different between the previous time and this time, the gradient is decelerated and the solution returns to the overlooked optimum solution.
I think it's named Resilient because this behavior makes it feel like you're rolling the ball (accelerating on a gradient, slowing down when the gradient changes direction and exerting a force in the opposite direction). ..
With a function like the Sigmoid function, learning will be difficult because it will be flat (gradient is almost 0) where the value exceeds a certain range (Flat Spot Problem. wiki / Flat_Spot_Problem))), applying this method also has the effect of preventing learning stagnation due to the weighting.
There are many variations of this technique itself. For details, please refer to here.
In addition to the various methods described above, it is also important to tune parameters such as the learning rate that adjusts the degree of error propagation and the momentum that adjusts the degree of influence of the previous layer, as with normal NN.
BPTT is generally slow to converge and takes a long time to learn. Therefore, hidden layer nodes are often used in small networks of about 3 to 20, and if it exceeds this, it may take several hours or even longer to learn.
RTRL (Real Time Recurrent Learning) Unlike BPTT, RTRL is a method of propagating errors in the future, which makes it suitable for online learning.

The error that occurred at time t updates the weight at the next time t + 1. In the figure above, the error is calculated and propagated at each time, but there is also a method of updating after a certain period of time (epoch). However, since the weight that must be updated at one time is larger than that of BPTT, the calculation load is high.
EKF (Extended Kalman Filter) It is EKF that applies the extended Kalman filter to the RNN and updates the weights. The extended Kalman filter is a non-linear extension of the Kalman filter that handles linear systems, and estimates the state of the system as follows.
$ x(n+1) = f(x(n)) + q(n) $ $ d(n) = h_n(x(n)) $
The above formula expresses the following.
- The next state $ x (n + 1) $ represents the input $ f (x (n)) $ from the previous state $ x (n) $ and $ q (n) $ (external noise). Is determined by
- The output of state $ x (n) $ is $ h_n (x (n)) $
The image is as shown in the figure below.

And RNN can be regarded as this extended Kalman filter. The figure below shows this.
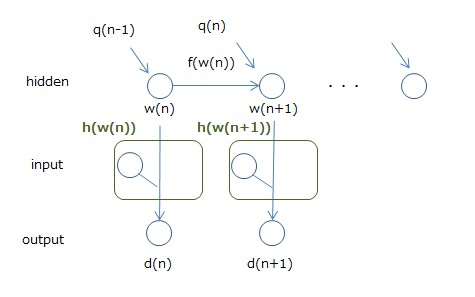
I think it's okay to have the weight $ w $ as the state and the output as $ d $. The problem is the input, but by considering it as part of the function $ h $ for calculating the output $ d $, we're saying it's an extended Kalman filter (actually the input and weights of the input). It's calculated in $ w $, so I don't think it's too difficult).
Then, the method of updating the state of the extended Kalman filter can be applied as it is to updating the state of the RNN, that is, the weight. The calculation formula for state update is quite complicated, so I will omit the details, but the method called EKF brings the extended Kalman filter method to RNN in this way. There is also a method for simplifying the calculation, which is a promising method, but like BPTT and RTRL, empirical tuning (learning rate, network configuration, etc.) is required to achieve accuracy.
RNN library
Pybrain is clearly supported by major libraries. A Recurrent Network Tutorial (http://pybrain.org/docs/tutorial/netmodcon.html#using-recurrent-networks) is also available.
It seems that it is possible with pylearn2, which is famous for deep learning, but as you can see from the path, it is still in the sandbox at the moment (2015/1), and it is in an uneasy state to actually use it.
lisa-lab/pylearn2 pylearn2/pylearn2/sandbox/rnn/models/tests/test_rnn.py
If you want to implement it yourself, the method using Theano is introduced.
Implementing a recurrent neural network in python gwtaylor/theano-rnn
This is a combination of RNN and RBM, but the implementation including the code is introduced.
Modeling and generating sequences of polyphonic music with the RNN-RBM Introduction to melody prediction and generation by RNN-RBM and music information processing
In addition, neuraltalk seems to be a model that learns an image and its explanation, and outputs an explanation when an image is given. It's more of a ready-made library than a library for building, but I think it's good to use it for this purpose.
RNN implementation
This time, I will implement RNN using pybrain, which has an implementation example as described above.
The latest version of PyBrain is 0.3.3 (as of January 2015). It seems that it has been [uploaded] on the PYPI site (https://pypi.python.org/pypi/PyBrain/0.3.3) ... but since it is 0.3.2 to enter from pip, git clone Drop the repository with and install it. Please refer to here for the procedure and dependent libraries.
The main dependency is Scipy. Python is written as 2.5, but I have confirmed that the test (python runtests.py) can be passed with Python 3.4.2 in my environment. Looking at issues etc., it seems that Python 3 has some unsupported parts, but there was no problem while using it (unless there is an error without knowing it ...).
For the predicted time series data, we generated and used the ball trajectory data. The ball bound data (www.cs.utoronto.ca/~ilya/code) initially used in this paper /2008/RTRBM.tar), but the operating environment is old as Python2, and if you believe the description in the README, it takes a week to learn (quote: the bouncing balls problems trains for a considerably longer amount of Since it was time (about a week on a fast computer ...)), I decided to generate and use a simple trajectory.
The building of the model is carefully described in the PyBrain tutorial, but the main description methods are summarized below.
Welcome to PyBrain’s documentation!
Network construction
Assemble using pybrain.structure. In the following, we are building a normal network with a bias term in 2-3-1.
Building Networks with Modules and Connections
from pybrain.structure import FeedForwardNetwork, LinearLayer, SigmoidLayer, BiasUnit, FullConnection
net = FeedForwardNetwork()
net.addInputModule(LinearLayer(2, name='i'))
net.addModule(BiasUnit('bias'))
net.addModule(SigmoidLayer(3, name='h'))
net.addOutputModule(LinearLayer(1, name='o'))
# connect nodes
net.addConnection(FullConnection(net['i'], net['h']))
net.addConnection(FullConnection(net['bias'], net['h']))
net.addConnection(FullConnection(net['bias'], net['o']))
net.addConnection(FullConnection(net['h'], net['o']))
It's easier to build with buildNetwork. The following is the same as the above process.
net = buildNetwork(2, 3, 1, bias=True, hiddenclass=SigmoidLayer)
Network learning
To do the training, first prepare a dataset. In the following, the data of output 1 is passed as ʻaddSample for input 2 according to the network constructed above (Note that ʻappendLinked and ʻaddSample` appearing in the document are equivalent. //github.com/pybrain/pybrain/blob/1dd5086a51c3c98497ef85b31178588a89d8951e/pybrain/datasets/unsupervised.py#L31)).
from pybrain.datasets import SupervisedDataSet
ds = SupervisedDataSet(2, 1)
ds.addSample((0, 0), (0,))
...
We will train with the prepared data set. trainer.train returns a double proportional to the error, which allows you to evaluate the fit to your training data.
Training your Network on your Dataset
from pybrain.supervised.trainers import BackpropTrainer
net = buildNetwork(2, 3, 1, bias=True, hiddenclass=TanhLayer)
trainer = BackpropTrainer(net, ds)
err = trainer.train()
Network prediction
Prediction is done with the ʻactivate` function.
net.activate([1, 2])
Building an RNN
In the case of RNN, it is almost the same as a normal network construction.
RNN uses RecurrentNetwork, and when making a recursive connection, connect with ʻaddRecurrentConnection`.
Then, the prediction is executed by ʻactivate after resetting once with net.reset () . For ʻactivate, in the above example, I predicted by entering the same value all the time, but in reality it was not true unless I entered the predicted value again and did it (in theory, even the first input). If there is, it can be predicted more and more after that, so I feel that there is no problem even if the initial value is left as it is ...).
This time I tried it with Elman and Jordan. Below is an image in Jordan. The coordinates of x and y and their respective accelerations are passed as inputs.

Acceleration is determined by the position of time t and the position of time t + 1, so I thought that it would learn well in the hidden layer ... but I added it as an input parameter because the accuracy was not achieved.
For the training data, we prepared several batches with different initial positions under the same initial acceleration, and trained / tested with them. Since the initial acceleration is the same for the training / test data, this model is a model that estimates what kind of trajectory will be drawn when the ball is placed at a certain point under that acceleration.
The accuracy is anxious, but the error with the test data was about 5.7 on average, which was not very good. Since this data predicts the trajectory of a ball bouncing in a 10x10 square, an error of 5.7 is a level that can be said to be almost completely wrong.
The animation shows that the feelings are moving to the extent that you can understand them, but there are a lot of things that can be completely reproduced. I also tried increasing or decreasing the hidden layers and nodes, but it didn't change.
Actual orbit
Predicted trajectory (quite close to the best)

The code used for verification is here. If you are the one who says I am, I am waiting for a pull request.
reference
- About RNN
- Recurrent neural network
- Types of artificial neural networks
- Hopfield network
- Echo state network
- What is the difference between Elman and Jordan neural networks
- Recurrent Neural Networks
- Bidirectional recurrent neural networks
- A tutorial on training recurrent neural networks, covering BPPT, RTRL, EKF and the "echo state network" approach
- A Direct Adaptive Method for Faster Backpropagation Learning: The RPROP Algorithm
- Papers on RNN implementation, etc.
- Modeling and generating sequences of polyphonic music with the RNN-RBM
- Modeling Temporal Dependencies in High-Dimensional Sequences:Application to Polyphonic Music Generation and Transcription
- ↑ Article explaining the paper in Japanese [Introduction to melody prediction and generation by RNN-RBM and music information processing](http://xiangze.hatenablog.com/entry/2014/09/28/ 143934)
- Continuous time recurrent neural networks for grammatical induction
- About PyBrain
- Welcome to PyBrain’s documentation!
Recommended Posts