Try using TensorFlow-Part 2-Convolutional Neural Network (MNIST)

This time, we will classify numbers by a convolutional neural network using MNIST.

MNIST MNIST is a dataset of handwritten text images from 0 to 9. This dataset contains 60,000 training data with an image size of 28x28. It contains 10,000 test data. Also, the same number of correct label data is included.

Use this dataset to find out what the numbers in the target image are.

Advance preparation

Download the MNIST sample code in advance.

Whole implementation code

The implementation content is based on TensorFlow's MNIST sample code. The contents of Deep MNIST for Experts have been imported and partially modified.

The entire implementation code is as follows. Place this source code directly under the mnist directory of the sample you downloaded earlier. ※ tensorflow/tensorflow/examples/tutorials/mnist

deep_mnist_softmax.py

from __future__ import absolute_import
from __future__ import division
from __future__ import print_function

import argparse
import sys

from tensorflow.examples.tutorials.mnist import input_data

import tensorflow as tf

#Weight variable
def weight_variable(shape):
  initial = tf.truncated_normal(shape, stddev=0.1)
  return tf.Variable(initial)

#Bias variable
def bias_variable(shape):
  initial = tf.constant(0.1, shape=shape)
  return tf.Variable(initial)

#Convolution
def conv2d(x, W):
  return tf.nn.conv2d(x, W, strides=[1, 1, 1, 1], padding='SAME')

#Pooling
def max_pool_2x2(x):
  return tf.nn.max_pool(x, ksize=[1, 2, 2, 1],
                        strides=[1, 2, 2, 1], padding='SAME')

def main(_):
  #Data acquisition
  mnist = input_data.read_data_sets('MNIST_data', one_hot=True)

  #placeholder creation
  x = tf.placeholder(tf.float32, [None, 784])
  y_ = tf.placeholder(tf.float32, [None, 10])

  #1st layer of convolution
  W_conv1 = weight_variable([5, 5, 1, 32])
  b_conv1 = bias_variable([32])
  x_image = tf.reshape(x, [-1,28,28,1])
  h_conv1 = tf.nn.relu(conv2d(x_image, W_conv1) + b_conv1)
  h_pool1 = max_pool_2x2(h_conv1)

  #2nd layer of convolution
  W_conv2 = weight_variable([5, 5, 32, 64])
  b_conv2 = bias_variable([64])
  h_conv2 = tf.nn.relu(conv2d(h_pool1, W_conv2) + b_conv2)
  h_pool2 = max_pool_2x2(h_conv2)

  #Fully connected layer
  W_fc1 = weight_variable([7 * 7 * 64, 1024])
  b_fc1 = bias_variable([1024])
  h_pool2_flat = tf.reshape(h_pool2, [-1, 7 * 7 * 64])
  h_fc1 = tf.nn.relu(tf.matmul(h_pool2_flat, W_fc1) + b_fc1)

  #Dropout layer
  keep_prob = tf.placeholder(tf.float32)
  h_fc1_drop = tf.nn.dropout(h_fc1, keep_prob)

  #Output layer
  W_fc2 = weight_variable([1024, 10])
  b_fc2 = bias_variable([10])
  y_conv = tf.matmul(h_fc1_drop, W_fc2) + b_fc2

  #Loss function (cross entropy error)
  cross_entropy = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(y_conv, y_))

  #Slope
  train_step = tf.train.AdamOptimizer(1e-4).minimize(cross_entropy)

  #accuracy
  correct_prediction = tf.equal(tf.argmax(y_conv, 1), tf.argmax(y_, 1))
  accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))

  #session
  sess = tf.InteractiveSession()
  sess.run(tf.global_variables_initializer())

  #training
  for i in range(5000):
    batch = mnist.train.next_batch(50)

    if i % 500 == 0:
      #Progress (every 500 cases)
      train_accuracy = accuracy.eval(feed_dict={x: batch[0], y_: batch[1], keep_prob: 1.0})
      print("step %d, training accuracy %f" % (i, train_accuracy))

    #Training execution
    train_step.run(feed_dict={x: batch[0], y_: batch[1], keep_prob: 0.5})

  #Evaluation
  print("test accuracy %f" % accuracy.eval(feed_dict={
    x: mnist.test.images, y_: mnist.test.labels, keep_prob: 1.0}))

if __name__ == '__main__':
  parser = argparse.ArgumentParser()
  parser.add_argument('--data_dir', type=str, default='/tmp/tensorflow/mnist/input_data',
                      help='Directory for storing input data')
  FLAGS, unparsed = parser.parse_known_args()
  tf.app.run(main=main, argv=[sys.argv[0]] + unparsed)

neural network

The processing flow of the above code and the shape of the neural network are as follows.

Process flow

shape

Implementation code details

The details of the implementation code are described below.

weight

#Weight variable
def weight_variable(shape):
  initial = tf.truncated_normal(shape, stddev=0.1)
  return tf.Variable(initial)

Initialize with a random value from the normal distribution as a weight variable.

--Bias

#Bias variable
def bias_variable(shape):
  initial = tf.constant(0.1, shape=shape)
  return tf.Variable(initial)

Initialize with a constant (0.1) as a bias variable.

shape [2, 3] [[0.1, 0.1, 0.1], [0.1, 0.1, 0.1]]

--Convolution

#Convolution
def conv2d(x, W):
  return tf.nn.conv2d(x, W, strides=[1, 1, 1, 1], padding='SAME')

Weight (filter size) Specify stride strides and padding paddingin the shape of W``` Perform convolution.

--Pooling

#Pooling
def max_pool_2x2(x):
  return tf.nn.max_pool(x, ksize=[1, 2, 2, 1],
                        strides=[1, 2, 2, 1], padding='SAME')

Specify stride strides and padding paddingin the shape of pooling size ksize``` Perform pooling.

ksize: How to specify the pooling size For 2x2 [1, 2, 2, 1] For 3x3 [1, 3, 3, 1]

--Data acquisition

  #Data acquisition
  mnist = input_data.read_data_sets('MNIST_data', one_hot=True)

Acquires MNIST data.

placeholder

 #placeholder creation
 x = tf.placeholder(tf.float32, [None, 784])
 y_ = tf.placeholder(tf.float32, [None, 10])

Input data: Create n x 784 as placeholder as `` `x. Label (correct) data: Create n x 10 as placeholder as y_```. The placeholder fills in the data at run time.

784 is the value when the 28x28 (= 784) image is treated as one dimension.

--Folding layer

#1st layer of convolution
W_conv1 = weight_variable([5, 5, 1, 32])
b_conv1 = bias_variable([32])
x_image = tf.reshape(x, [-1,28,28,1])
h_conv1 = tf.nn.relu(conv2d(x_image, W_conv1) + b_conv1)
h_pool1 = max_pool_2x2(h_conv1)

#2nd layer of convolution
W_conv2 = weight_variable([5, 5, 32, 64])
b_conv2 = bias_variable([64])
h_conv2 = tf.nn.relu(conv2d(h_pool1, W_conv2) + b_conv2)
h_pool2 = max_pool_2x2(h_conv2)

Here, the process is performed according to the following flow.

Convolution with filter size (5x5) and 32 outputs
Bias addition
Adapt the activation function ReLU
Pooling in pooling size (2x2)
To the second layer
Convolution with filter size (5x5) and output 64
Perform the same treatment as the first layer to the fully connected layer.

--Full bond layer

#Fully connected layer
W_fc1 = weight_variable([7 * 7 * 64, 1024])
b_fc1 = bias_variable([1024])
h_pool2_flat = tf.reshape(h_pool2, [-1, 7 * 7 * 64])
h_fc1 = tf.nn.relu(tf.matmul(h_pool2_flat, W_fc1) + b_fc1)

[7 * 7 * 64, 1024]Is7 * 7However, the size that was pooled in the second layer of convolution, 64However, the number of outputs in the second layer of convolution,1024Is the number of outputs of the fully connected layer.

Here, the process is performed according to the following flow.

Shape the output result of the second layer of convolution into two dimensions for multiplication.
Multiply by the convolutional second layer output (n, 7x7x64) and the weight (7x7x64, 1024)
Bias addition
Adapt the activation function ReLU
To the next layer

--Dropout layer

#Dropout layer
keep_prob = tf.placeholder(tf.float32)
h_fc1_drop = tf.nn.dropout(h_fc1, keep_prob)

keep_probSpecifies the drop rate.

Because it is a placeholder, enter the drop rate at runtime.

--Output layer

#Output layer
W_fc2 = weight_variable([1024, 10])
b_fc2 = bias_variable([10])
y_conv = tf.matmul(h_fc1_drop, W_fc2) + b_fc2

Specify the number of classifications to output, 10.

--Loss function / gradient / accuracy

#Loss function (cross entropy error)
cross_entropy = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(y_conv, y_))

#Slope
train_step = tf.train.AdamOptimizer(1e-4).minimize(cross_entropy)

#accuracy
correct_prediction = tf.equal(tf.argmax(y_conv, 1), tf.argmax(y_, 1))
accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))

Specify the cross entropy error as the loss function Specify Adam for the gradient. `` `1e-4``` is the learning rate. The accuracy is the average of the correct answers (number of correct answers / n).

--Session

#session
sess = tf.InteractiveSession()
sess.run(tf.global_variables_initializer())

Create a session. here,

`sess.run(tf.global_variables_initializer())At tf.Initializing Variable.`




 - training

```python
#training
for i in range(5000):
  batch = mnist.train.next_batch(50)

  if i % 500 == 0:
    #Progress (every 500 cases)
    train_accuracy = accuracy.eval(feed_dict={x: batch[0], y_: batch[1], keep_prob: 1.0})
    print("step %d, training accuracy %f" % (i, train_accuracy))

  #Training execution
  train_step.run(feed_dict={x: batch[0], y_: batch[1], keep_prob: 0.5})

Set the number of trainings to 5000 (specify less because it takes time) In one training, read 50 training data at a time and execute train_step. In addition, the accuracy is printed out every 500 times as a progress. (For the accuracy output of this progress, the training data is used as it is as the calculation data. Moreover, the number of data is as small as 50, so the reliability is low.)

Supplement ・ Mnist.train.next_batch ()` `` shuffles the data when it is read to the end. Read the data from the beginning again. - Feed_dict = {x: batch [0], y_: batch [1] `` `is inputting placeholder data. - Keep_prob: 0.5 specifies a drop rate of 50%, and 1.0 will not drop. Specify 1.0 for evaluation and forecasting.

--Evaluation

#Evaluation
print("test accuracy %f" % accuracy.eval(feed_dict={
  x: mnist.test.images, y_: mnist.test.labels, keep_prob: 1.0}))

Here, the accuracy is calculated using 10,000 test data.

`keep_prob is 1.0 is specified.`




## Run

 Run the code.

python deep_mnist_softmax.py

 * When executing in the environment created in the previous [Entry](http://qiita.com/fujin/items/93aa9144d756eb85004d), execute after starting the virtual environment.

## result

 The execution result is as follows.
 The accuracy has increased to 98.57%.
 Increasing the number of trainings should improve the accuracy a little more.

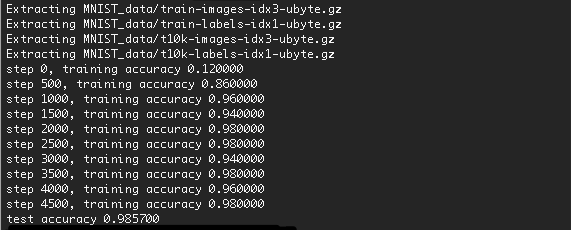
 ![sc_2017-02-001.png](https://qiita-image-store.s3.amazonaws.com/0/134550/55eafe53-65bd-e8bd-b73c-1e66b96f2ee0.png)

 > It will take some time for the first time because the data will be downloaded.

 As mentioned above, this time, we performed number classification by convolutional neural network using MNIST.