Design Pattern #Strategy

I practiced design patterns so that I could write code that was conscious of design. Other Design Patterns will be released frequently.

Preface

Introduction to Design Patterns Learned in Java Language has been changed from Java to Python. (Python is 3.4.2)
The code is on github (some of them still don't work)

The primary goal is to understand when, what, and how to use design patterns. (I'm new to Java or a statically typed language, and I don't have a long history of python, so I think there are some things that aren't like Pythonista. If you have any suggestions, please teach me.)

This time, the pattern Strategy regarding behavior.

What is Strategy?

The part that implements the algorithm can be exchanged in a sneak peek. A pattern that makes it easy to switch algorithms and solve the same problem differently.

That's because the Strategy pattern consciously separates the algorithm part from the other parts. And only the interface (API) part with the algorithm is specified. Then, the algorithm is used by delegation from the program. You can easily switch between algorithms by using the loose ties of delegation.

You can use the Strategy pattern when many behaviors appear as multiple conditional statements.

Overview

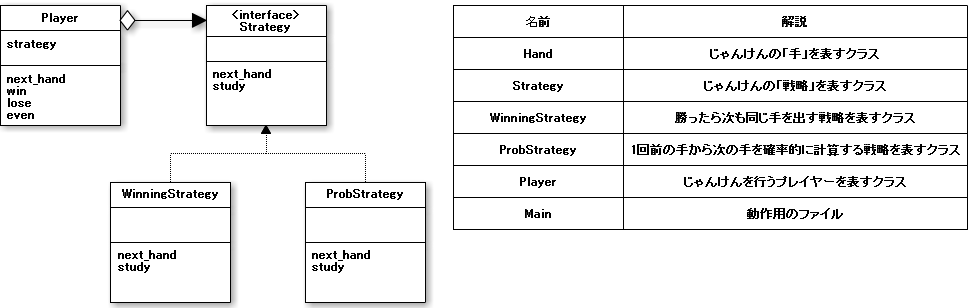
The sample program created here is for playing "rock-paper-scissors" on a computer. I thought of two methods as the "strategy" of rock-paper-scissors. One is the method of "if you win, you will do the same move next time" (WinningStrategy), and the other is the method of "probabilistically calculating the next move from the previous move" (ProbStrategy).

Overall class diagram

`hand.py`


class Hand():
    HANDVALUE_ROCK = 0
    HANDVALUE_SCISSORS = 1
    HANDVALUE_PAPER = 2
    NAMES = ['Goo', 'Choki', 'Par']
    HANDS = [HANDVALUE_ROCK,
             HANDVALUE_SCISSORS,
             HANDVALUE_PAPER]

    def __init__(self, handvalue):
        self.__handvalue = handvalue

    def get_hand(self, handvalue):
        return self.HANDS[self.__handvalue]

    def is_stronger_than(self, h):
        return self.__fight(h) == 1

    def is_weaker_than(self, h):
        return self.__fight(h) == -1

    def __fight(self, h):
        if self.__handvalue == h.__handvalue:
            return 0
        elif (self.__handvalue + 1) % 3 == h.__handvalue:
            return 1
        else:
            return -1

    def to_string(self):
        return self.NAMES[self.__handvalue]

The Hand class is a class that represents the "hand" of rock-paper-scissors. Inside the class, goo is 0, choki is 1, and par is 2. Save this as a field (handvalue) that represents the value of the hand.

Only three instances of the Hand class can be created. Initially three instances are created and stored in the array HANDS.

You can get an instance using the class method get_hand. If you give a hand value as an argument, the instance will be the return value.

is_stronger_than and is_weaker_than compare hand strength. Use when you have two hands, hand1 and hand2.

Inside this class, it is a method called fight that actually determines the strength of the hand. The value of the hand is used to judge the strength. The (self.__handvalue + 1)% 3 == h.__handvalue used here is the value of the hand of self plus 1 is the value of the hand of h (if self is goo, h is choki, self If is choki, h is par, and if self is par, h is goo), then self is stronger than h. The operator% is used to take the remainder of 3 because we want it to be goo (0) when 1 is added to par (2).

`strategy.py`


from abc import ABCMeta, abstractmethod


class Strategy(metaclass=ABCMeta):

    @abstractmethod
    def next_hand():
        pass

    @abstractmethod
    def study(win):
        pass

The Strategy interface is a collection of abstract methods for rock-paper-scissors "strategy".

next_hand is a method for "getting the next move". When this method is called, the class that implements the Strategy interface decides the "next move".

study is a method for learning "whether or not you won by the hand you just put out". If the previous next_hand method call wins, call it as study (True). If you lose, call it as study (False). As a result, the class that implements the Strategy interface changes its internal state and uses it as a material to determine the return value of the next_hand method from the next time onward.

`winning_strategy.py`


import random
from hand import Hand
from strategy import Strategy


class WinningStrategy(Strategy):

    __won = False
    __prev_hand = 0

    def __init__(self, seed):
        self.__rand = seed

    def next_hand(self):
        if not(self.__won):
            self.__prev_hand = Hand(self.__rand).get_hand(random.randint(0, 3))
        return self.__prev_hand

    def study(self, win):
        self.__won = win

The WinningStrategy class is one of the classes that implements the Strategy interface. Implementing the Strategy interface means implementing two methods, next_hand and study.

In this class, if you win the previous game, you will take the same strategy next time (goo for goo, par for par). If you lose the previous game, the next move will be decided using random numbers.

The rand field holds the random numbers that this class uses when it needs them.

The won field holds the result of the previous game. If you win, it will be True, if you lose, it will be False.

The prev_hand field holds the hand that was put out in the previous game.

`prob_strategy.py`


import random
from hand import Hand
from strategy import Strategy


class ProbStrategy(Strategy):

    __prev_hand_value = 0
    __current_hand_value = 0
    __history = [[1, 1, 1], [1, 1, 1], [1, 1, 1]]

    def __init__(self, seed):
        self.__rand = seed

    def next_hand(self):
        bet = random.randint(0, self.__get_sum(self.__current_hand_value))
        hand_value = 0
        if bet < self.__history[self.__current_hand_value][0]:
            hand_value = 0
        elif bet < self.__history[self.__current_hand_value][0] + \
                self.__history[self.__current_hand_value][1]:
            hand_value = 1
        else:
            hand_value = 2

        self.__prev_hand_value = self.__current_hand_value
        self.__current_hand_value = hand_value

        return Hand(hand_value).get_hand(hand_value)

    def __get_sum(self, hv):
        total = 0
        for i in range(0, 3):
            total += self.__history[hv][i]
        return total

    def study(self, win):
        if win:
            self.__history[self.__prev_hand_value][self.__current_hand_value] \
                += 1
        else:
            self.__history[self.__prev_hand_value][(self.__current_hand_value + 1) % 3] \
                += 1
            self.__history[self.__prev_hand_value][(self.__current_hand_value + 2) % 3] \
                += 1

The ProbStrategy class is another concrete "strategy". The next move is always decided by random numbers, but we use the history of past wins and losses to change the probability of each move.

The history field is a table for probability calculation that reflects past wins and losses. history is a two-dimensional array of integers, and the subscripts of each dimension have the following meanings.

history [Last hand] [This time] The higher the value of this formula, the higher the winning percentage in the past.

If you write in detail. history [0] [0] Goo, Goo and the number of past wins when you put out history [0] [1] Goo, Choki and the number of past wins when you put out history [0] [2] Goo, Par and the number of past wins when you put out

Suppose you put out a goo last time. At that time, what I will give next is calculated with probability from the above values of histroy [0] [0], history [0] [1], and history [0] [2]. In short, add the values of these three expressions (get_sum method), calculate the number from 0, and then decide the next move based on it (next_hand method).

For example The value of history [0] [0] is 3 The value of history [0] [1] is 5 The value of history [0] [2] is 7 in the case of. At this time, the ratio of goo, choki, and par is set to 3: 5: 7, and the next move is decided. Obtain a random number between 0 and 15 (15 is a value of 3 + 5 + 7), Goo if 0 or more and less than 3 Choki if 3 or more and less than 8 Par if 8 or more and less than 15 will do.

The study method updates the contents of the history field based on the outcome of the hand returned by the next_hand method.

`player.py`


class Player():

    __wincount = 0
    __losecount = 0
    __gamecount = 0

    def __init__(self, name, strategy):
        self.__name = name
        self.__strategy = strategy

    def next_hand(self):
        return self.__strategy.next_hand()

    def win(self):
        self.__strategy.study(True)
        self.__wincount += 1
        self.__gamecount += 1

    def lose(self):
        self.__strategy.study(False)
        self.__losecount += 1
        self.__gamecount += 1

    def even(self):
        self.__gamecount += 1

    def to_stirng(self):
        return '[{0}: {1} games {2} win {3} lose]'.format(self.__name,
                                                          self.__gamecount,
                                                          self.__wincount,
                                                          self.__losecount)

The Player class is a class that represents a person who plays rock-paper-scissors. The Player class is given a "name" and a "strategy" to instantiate. The next_hand method is for getting the next move, but it is your "strategy" that actually determines the next move. The return value of the strategy's next_hand method will be the return value of the Player's next_hand method. The next_hand method "delegates" what it should do to Strategy.

The Player class calls the study method through the startegy field in order to use the results of winning (win), losing (lose), and drawing (even) games in the next game. Use the study method to change the internal state of the strategy. wincount, losecount and geamecount record the number of wins of a player.

`main.py`


import random
import sys
from winning_strategy import WinningStrategy
from prob_strategy import ProbStrategy
from player import Player
from hand import Hand


def main():
    try:
        if int(sys.argv[1]) >= 3:
            seed1 = random.randint(0, 2)
        else:
            seed1 = int(sys.argv[1])

        if int(sys.argv[2]) >= 3:
            seed2 = random.randint(0, 2)
        else:
            seed2 = int(sys.argv[2])

        player1 = Player('Taro', WinningStrategy(seed1))
        player2 = Player('Hana', ProbStrategy(seed2))
        for i in range(0, 10):  # 10000
            next_hand1 = Hand(player1.next_hand())
            next_hand2 = Hand(player2.next_hand())
            if next_hand1.is_stronger_than(next_hand2):
                print('Winner : {0}'.format(player1.to_stirng()))
                player1.win()
                player2.lose()
            elif next_hand2.is_stronger_than(next_hand1):
                print('Winner : {0}'.format(player2.to_stirng()))
                player1.lose()
                player2.win()
            else:
                print('Even ...')
                player1.even()
                player2.even()

        print('Total result:')
        print(player1.to_stirng())
        print(player2.to_stirng())

    except IndexError:
        print('Check args size, does not work')
        print('usage: python main random_seed1 random_seed2')
        print('Example: python main.py 314 15')

if __name__ == "__main__":
    main()

Execution result

python main.py 21  3
Winner : [Hana: 0 games 0 win 0 lose]
Even ...
Winner : [Hana: 2 games 1 win 0 lose]
Winner : [Taro: 3 games 0 win 2 lose]
Even ...
Winner : [Taro: 5 games 1 win 2 lose]
Even ...
Winner : [Hana: 7 games 2 win 2 lose]
Winner : [Taro: 8 games 2 win 3 lose]
Winner : [Hana: 9 games 3 win 3 lose]
Total result:
[Taro: 10 games 3 win 4 lose]
[Hana: 10 games 4 win 3 lose]

Summary

The Strategy pattern consciously separates the algorithm part from the other parts. Since it uses a loose connection called delegation, it is easy to switch algorithms if you do not change the interface part.

Design Pattern #Strategy

Preface

What is Strategy?

Overview

Overall class diagram

hand.py

strategy.py

winning_strategy.py

prob_strategy.py

player.py

main.py