Gold needle for when it becomes a stone by looking at the formula of image processing

Image processing is difficult. Looking at Instagram's beautiful filters, Google's Photo Sphere, and those services, the images look interesting! An image processing book that opened with excitement. We had no choice but to petrify the mathematical formulas listed there, but what else is left to the voice whispered in our ears, "OpenCV will do the difficult things, right?" I could have done it.

I hope that this article will show the way (in terms of items, gold needles) to those who want to overcome those days when they had to petrify and understand the basic theory while using OpenCV. think. The scope of coverage is in Chapter 2 of Practical Computer Vision, which is the basis of all processing. Equivalent). In addition, since this article itself is written while being understood by me as a beginner, I would appreciate it if advanced image processing adventurers could point out any mistakes.

What are the feature points of the image?

Why can humans assemble jigsaw puzzles? Thinking about it, we can think of it as understanding the characteristics of each piece of the puzzle, finding similar and continuous characteristics, and connecting them together. Similarly, you can combine multiple photos into a panoramic photo because you find and connect common features between the photos.

image CS231M Mobile Computer Vision Class,Lecture5, Stitching + Blending, p4~

If you think about these "feature points" more and more simply, you can finally summarize them into the following three points.

image

And, considering the composition of panoramic photos as described above, it is necessary to follow the following rules when finding this "feature point".

Regarding reproducibility, for example, if the feature points that are recognized when the angle at which the photograph is taken changes drastically, the process of connecting the feature points will break down.

image

Therefore, it is better to be able to recognize robust feature points ** that do not change with the angle or magnification of the image.

With regard to distinctiveness, if the recognized feature points cannot be uniquely identified, it will be difficult to know which one to match.

image

Therefore, it is important to have a representation method that allows each feature point to be uniquely identified.

This is exactly what is required for Feature Detection and Feature Description. In other words, detecting "a robust feature point that does not change with the angle or magnification of the image" (Feature Detection) and expressing it with a "uniquely identifiable expression method" (Feature Description) is the image. It is the goal of recognizing feature points.

Now, let's look at the detection of feature points and the expression method of feature points in order.

Feature Detection

The procedure for detecting feature points is generally "detecting edges" and then "detecting corners" where edges are concentrated.

edge detection

Specifically, the edge is the "point where the brightness changes significantly". As a simple example, consider an image of a black tile with a white circle. If you plot the brightness on the red line drawn from the side as shown below along the coordinate axes, you should get a graph in which the brightness jumps in the white circle in the middle.

image

Here, what we want to detect is the edge, that is, the point on the graph that changes significantly from dark-> bright, bright-> dark. In order to know the degree of change at a certain point, let's calculate the rate of change from the values of the points before and after that point.

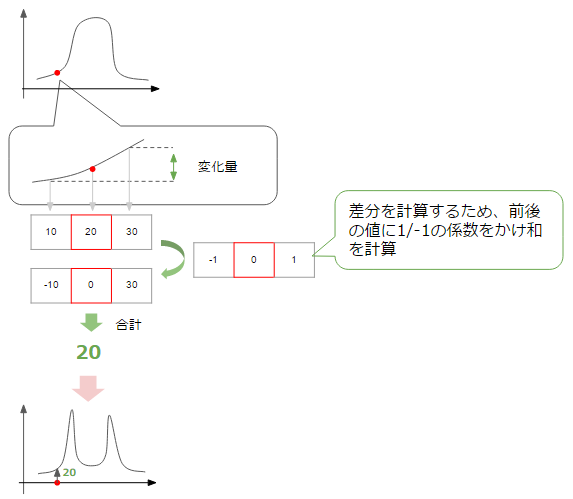
image

Then, as shown in the above figure, you can get a graph in which the rate of change is increasing at the point where the change is large, that is, the part corresponding to the edge (the amount of change has +-, but here the absolute value is plotted. Please think). Right now, we are thinking about the amount of change in the horizontal direction of the figure, but the same can be said for the vertical direction.

Ultimately, it seems that edge can be detected by summing the amount of change in both the horizontal and vertical directions (usually the square root of the sum of squares) and collecting points whose value is larger than a certain threshold.

This is the basic idea of edge detection, and although edge detection is possible with this alone, there are some techniques for more accurate detection, so let's take a look at it.

Smoothing

This is a method that considers the peripheral part when calculating the amount of change. Roughly speaking, it's like taking an average. By averaging, the change in value can be smoothed (smoothing), and as a result, smoothly connected edges can be detected.

The figure below shows how the amount of change in the horizontal direction is calculated by taking into account the amount of change at adjacent points. Smoothing is achieved by summing a total of three changes.

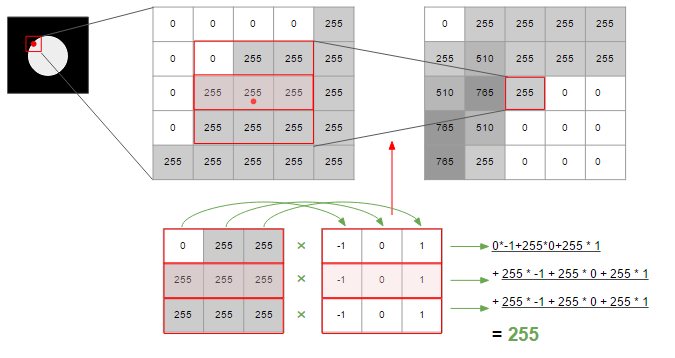
image

In the above figure, in order to calculate the amount of change, it is calculated using a matrix containing the value of -1/0/1 of 3 * 3. The matrix and processing for calculating such changes are called ** filters **.

There are various types of this filter, and the one used in the above figure is the Prewitt filter. Sobel filters focus more on what is adjacent to the center than Prewitt, and Gaussian uses a function of normal distribution to allow the center to be the apex and the coefficients to be gently multiplied toward the edges. The Canny method, which is often used to detect edges, is a method that uses this Gaussian filter.

image

Note that it is necessary to perform interpolation for the edge of the image because there are no adjacent points. There are the following methods for this interpolation method.

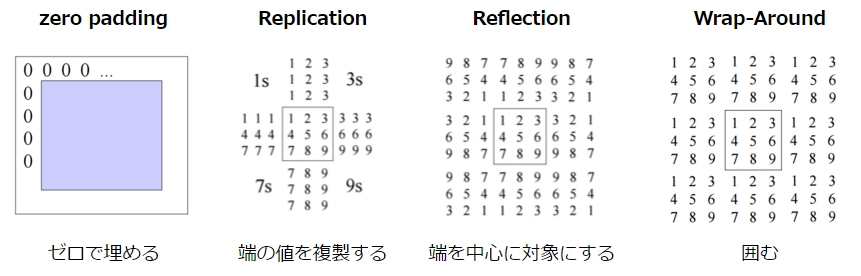image CSE/EE486 Computer Vision I, Lecture3, p26~

That's all for edge detection. I will summarize the contents so far.

Corner detection

Next is the detection of corner. Here, we will explain the Harris Corner Detector, which is often used for corner detection. This is a method that makes good use of the characteristics of the matrix, and intuitively gives an image close to principal component analysis.

image

I will leave the detailed explanation of principal component analysis to other articles, but the following two points are important.

Applying this to Harris, the "data" is, of course, a summary of the amount of change in each of the horizontal and vertical directions at a certain point. Then, from the explanation of principal component analysis above, it can be inferred as follows.

This makes it possible to detect edges first, and if there are "multiple eigenvectors with large eigenvalues", then it means that there are multiple edges, that is, corners. Assuming that the eigenvalues are $ \ lambda1 $ and $ \ lambda2 $, respectively, they can be classified as follows according to the size of the values.

image CSE/EE486 Computer Vision I, Lecture 06, Corner Detection, p19

I will also explain the formula. First, a point $ I (x, y) $ on the image $ I $ and a point $ I (x + u, y + v) moved by $ u $ in the $ x $ direction and $ v $ in the $ y $ direction. If the amount of change between) $ is $ E (u, v) $, the formula can be expressed as follows.

E(u, v) = \sum_{x, y} w(x, y) [I(x+u, y+v) - I(x, y)]^2

$ w (x, y) $ is a window function, which is a filter (Gaussian). The image is that the amount of change is $ [I (x + u, y + v) --I (x, y)] ^ 2 $, and this is smoothed with $ w (x, y) $ to calculate the amount of change. is. Approximating this formula using Taylor expansion is as follows (expansion formula is omitted. If you are interested, please refer to the lecture material linked above).

E(u, v) \simeq [u, v] M \begin{bmatrix} u \\ v \end{bmatrix}

Where $ M $ is:

M = \sum_{x, y} w(x, y) \begin{bmatrix} I_X^2 & I_x I_y \\ I_x I_y & I_y ^2 \end{bmatrix}

$ I_x $ and $ I_y $ are the differences on the x-axis and y-axis, respectively, and the square of $ [I_x, I_y] $ gives the above matrix part. What you are doing is the same as $ [I (x + u, y + v) --I (x, y)] ^ 2 $ in the above formula. And this is the "matrix that describes the amount of change", and by decomposing this into singular values, it is possible to judge the edge and corner as described at the beginning.

However, calculating the eigenvalues is a lot of work, so try not to calculate them where you don't need them. The following indicators are used for this purpose.

R = det M -k(trace M)^2

det M = \lambda1 \lambda2

trace M = \lambda1 + \lambda2

$ k $ is a constant, about 0.04 ~ 0.06. It can be classified as follows according to the value of R.

The figure is as follows.

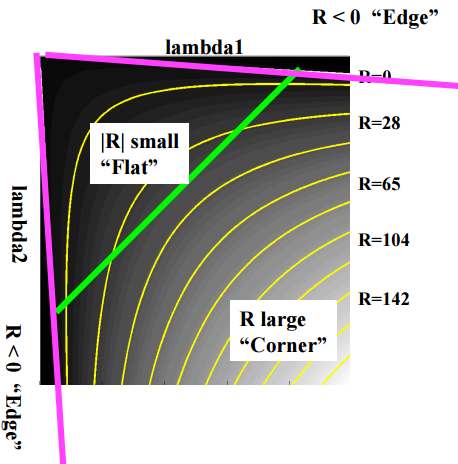image CSE/EE486 Computer Vision I, Lecture 06, Corner Detection, p22

Now you can detect the corner quickly. Here is a summary of corner detection.

Since Harris considers the eigenvectors that are the orientation of the edge, it is robust against the tilt of the image. However, it is not robust when it comes to scale. This is because the corners become looser as you expand, making it harder to distinguish the edges.

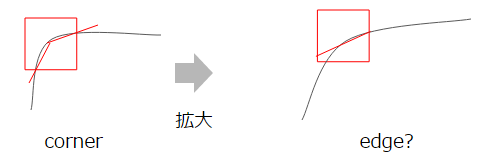
image

FAST is a devised method to overcome this. I will omit the details, but it is a method to recognize a series of n points darker or brighter than the center point. This is literally a FAST technique and is robust against rotation and expansion.

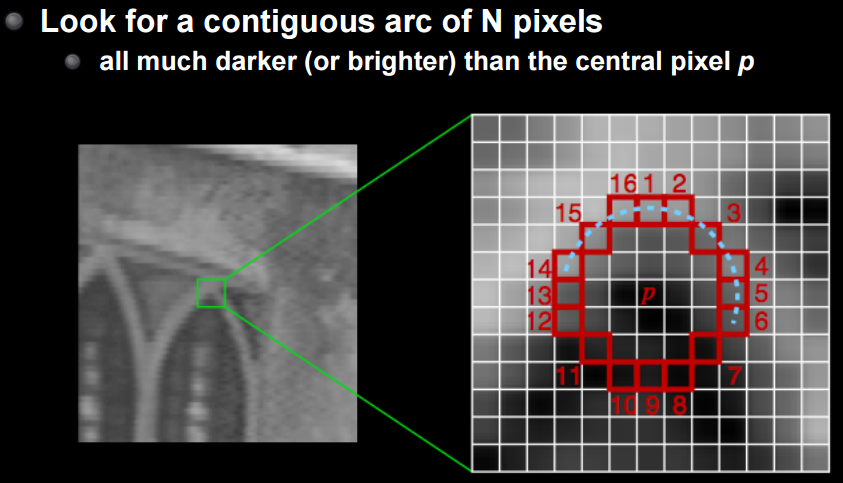image CS231M Mobile Computer Vision Class,Lecture5, Stitching + Blending, p24

Feature Description

The feature points can now be detected. Next time, I would like to be able to match images by creating a unique feature expression and Feature Description using the feature points.

As I mentioned a little, the following three characteristics are desirable for this Feature Description.

Since Translation simply changes its position, it is relatively easy to deal with, and as mentioned in Harris in the previous section, Rotation is also quite good. However, it is difficult to support Scaling. As you can see from the figure below, the information in the image changes significantly depending on the magnification.

image CSE/EE486 Computer Vision I, Lecture 31, Object Recognition : SIFT Keys, p31

In the first place, if you expand it, it is obvious that the information will be lost if you do not expand the matching range accordingly. This is because the area that fits in the same range changes.

image

In other words, it is necessary to consider the scale to satisfy the above three characteristics. In Harris, only "direction" and "strength" were used from the eigenvectors and eigenvalues, but here we add "scale", that is, what enlargement value is obtained. The image looks like the following.

image

The SIFT method enables the detection and description of feature points that take this scale into consideration.

SIFT (Scale Invariant Feature Transform)

The heart of SIFT is the extraction of feature points for each scale. The method used for this is LoG / DoG. Log is an abbreviation of Laplacian of Gaussian, and the point with the largest amount of change in the image smoothed by the Gaussian filter is obtained by the second derivative (= Laplacian). Since Gaussian is as described in Smoothing, I will briefly explain why the point with the maximum amount of change is obtained by the second derivative (= Laplacian).

image

Think of differentiation as simply finding the amount of change at a certain point. Then you can see the following.

In other words, the point where $ I (x)'' = 0 $ is raised as the point with the largest amount of change and the feature point. The filter equivalent to applying this second derivative is called the "Laplacian filter", and the closer the value is to 0, the higher the possibility of feature points.

Then, returning to LoG, as the name suggests, this is a method of smoothing with a Gaussian filter and then finding the point with the maximum amount of change = feature point with a Laplacian filter. And since LoG uses a Gaussian filter, you can adjust its $ \ sigma $ (variance). The larger $ \ sigma $ is, the stronger the smoothing will be, so it will only be possible to detect where points with large changes are gathered. This is the other way around, and as you may have noticed, it plays the same role as just manipulating the magnification.

image

スクリーンショット 2016-02-04 13.37.57.png

CSE/EE486 Computer Vision I, Lecture 11, LoG Edge and Blob Finding, p19

SIFT detects feature points by preparing multiple hierarchies adjusted for this $ \ sigma $ (scale space). The following is the figure.

スクリーンショット 2016-02-04 13.45.53.png

Here, in order to simplify the calculation of LoG, the approximation is performed by the difference between the two layers with different $ \ sigma $. This is the DoG (Difference of Gaussian). The found feature points are compared with the front and back scales to see if they are robust against the scale (compared with 8 points around and 9 points each on the front and back scales, for a total of 26 points).

Now you can see the robust features on the scale. The rest is the "strength" and "direction" of the amount of change at this feature point, which is obtained from the amount of change and its angle.

スクリーンショット 2016-02-04 13.30.42.png

Here, SIFT considers not only a single feature point, but also 16 * 16 cells centered on it (the size of this "mass" is called [bin size](http: // www). .vlfeat.org/api/sift.html)).

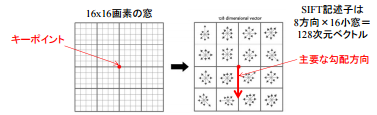image Semantic multimedia processing A2, p4

Divide it into 4x4 areas, and create a histogram with the vertical axis representing the amount of change (magitude of the amount of change) and the horizontal axis oriented (= the angle of the gradient of the amount of change).

image CSE/EE486 Computer Vision I, Lecture 31, Object Recognition : SIFT Keys, p24

The above figure is summarized from 0 to 36 (corresponding to 360 degrees), but finally it is summarized in 8 directions. Then, a vector is created in which each 4 * 4 window has elements in 8 directions. This 128-dimensional vector is the SIFT Vector, which is a feature point description with three characteristics: it is robust to "scale" and "strength" and "direction" are known.

By using this SIFT Vector, it becomes possible to match feature points with extremely high accuracy.

Evolution of feature point detection method

The methods for detecting and describing feature points listed above are evolving year by year. The following is the evolution of the method before and after the appearance of SIFT. You can see the process of obtaining features that are robust against rotation and scale.

image MIRU2013 Tutorial: SIFT and subsequent approaches, p5

This is the evolution after SIFT. A technique called SURF, which accelerates SIFT, is also often used. Both SIFT and SURF are patented **. SIFT patent expired on March 6, 2020, and OpenCV also [out of NON FREE](https://github.com/ opencv / opencv_contrib / pull / 2449), but there is still a patent fee for using SURF. Therefore, I have explained so far, but it seems that ORB and AKAZE added in OpenCV 3.0 are good for actual use. Nothing is faster than SIFT / SURF.

image MIRU2013 Tutorial: SIFT and subsequent approaches, p93

If you understand the basic methods introduced this time, it will be easier to understand what has been improved when new methods appear in the future.

Feature point matching

The detected feature points can be used for various purposes. As a typical example, I would like to introduce the method used for image matching.

First, when matching images, the basic flow is to cut out the area around the feature point to be compared (this cut out is called a patch) and check if it is also in the other image. Become. There are two types of how to use this patch:

The image is as shown in the figure below.

image

In any case, when making a comparison, you need a function to measure similarity. * Since it is difficult to calculate the similarity for the entire range of the image, it is necessary to narrow down the search range, but I will not touch it here.

The following are typical indicators for measuring similarity.

** SSD ** is the simplest index, and if you look at the difference between Templates and Features and it is close to 0, it is considered to be similar. For the distance, that is, the threshold, the ratio to the most matching feature point is often used. ** NCC **, or cross-correlation, is a measure of similarity and can be obtained by calculating the dot product. For example, vectors that are completely unrelated (= independent of each other) should be orthogonal, and the inner product of the orthogonal vectors is 0. On the contrary, if it is other than 0, there is a positive or negative correlation. Then, the normalized cross-correlation is obtained by normalizing (mean 0, variance 1) and then taking the cross-correlation.

I will also write a formula

SSD(I_1, I_2) = \sum_{[x, y] \in R} (I_1(x, y) - I_2(x, y))^2 \\
C(I_1, I_2) = \sum_{[x, y] \in R} I_1(x, y) I_2(x, y) \\
NCC(I_1, I_2) = \frac{1}{n - 1}\sum_{[x, y] \in R} \frac{(I_1(x, y) - \mu_1)}{\sigma_1} \cdot \frac{(I_2(x, y) - \mu_2)}{\sigma_2}

NCC is a process that is filtered by Template due to the nature of taking the inner product. The following is an example of actual processing, and you can see that the part that matches the Template is reacting.

image CSE/EE486 Computer Vision I, Lecture 7, Template Matching, p7

If you want to perform more strict matching, you can match not only A-> B but also B-> A and use only the ones that are judged to match on both sides. By using this feature point matching, it is possible to create panoramic photos, classify and search images.

Implementation in OpenCV

Finally, I will introduce how to implement it in OpenCV. I have a sample written in Jupyter notebook in the following repository.

icoxfog417/cv_tutorial_feature

Although it is an installation of OpenCV, Anaconda (conda) is recommended for Windows. Not only numpy and matplotlib, but also OpenCV itself can be installed in one shot from the following.

menpo/Packages/opencv3

For implementation, I referred to the following OpenCV official tutorial.

The code itself is just a few lines, but it often doesn't detect well without parameter adjustments (especially SIFT), and parameter adjustments still require a theoretical understanding. In that sense, I think that a theoretical understanding is indispensable for mastering OpenCV in the true sense of the word.

image

We hope that the explanations introduced this time will help you to solve petrification and become a true image processing master.

Research trends

Recently, the Convolutional Neural Network (CNN) has appeared, and in terms of feature extraction from images, I think the first thing to worry about is which is better, the ancient method or CNN. First, I would like to introduce a survey on that point.

CNN still has some handicap in terms of learning required and processing speed, but it is still strong in that it can perform various tasks with high accuracy. Many of the ideas contained in the methods represented by SIFT are still useful, so it is proposed in the above paper that we can go higher by combining them.

Research on feature extraction using DNN includes the following.

References

Recommended Posts

Gold needle for when it becomes a stone by looking at the formula of image processing
Image processing? The story of starting Python for
Try image processing with Python when asked for entertainment at a wedding ceremony
Take a peek at the processing of LightGBM Tuner
Image crawling summary performed at the speed of a second
The image display function of iTerm is convenient for image processing.
What to do when a part of the background image becomes transparent when the transparent image is combined with Pillow
A collection of examples for when you're confused by Python's slice notation
How to save the feature point information of an image in a file and use it for matching
Grayscale by matrix-Reinventor of Python image processing-
The story of blackjack A processing (python)
When increasing the available memory of node, it may be limited by vm.max_map_count
Half a year when the humanities of Gorigori learned AI almost by themselves
3. Natural language processing with Python 3-3. A year of corona looking back at TF-IDF