Make a DNN-CRF with Chainer and recognize the chord progression of music
This is the 11th day of Chainer Advent Calendar.
What is chord progression recognition?
When we make music, we can get a richer sound by layering sounds with different pitches. This is called a chord. By changing (developing) the chords as time goes by, the diaphysis of music is completed. This is the chord progression. Chord progression is probably the most important factor when listening to music. If you know the chord progression, you can almost reproduce the accompaniment on the guitar or keyboard. Well, in short, the text is about letting the computer copy by ear automatically. When actually copying by ear, I make a rough judgment such as "Am is ringing in this measure, and C is next ...". I don't think about the enumeration of notes or the rhythm. The chords can be clearly defined by the constituent notes, but when the actual music signal is decomposed into the frequency range, the pitch is unclear, the overtones are mixed, and the non-constituent notes are usually mixed, so it is not easy to distinguish. Therefore, the current situation is that we tend to rely on data-driven methods. It is one of the basic tasks in the music information processing (MIR) area and is useful for genre discrimination, sentiment analysis and cover song recognition. It is also one of the tasks of the annual music information processing competition MIREX. MIREX 2016:Audio Chord Estimation Summary of participating algorithms Well, it's a normal series labeling problem that is formally normal, so I hope it will be a reference for implementing various similar tasks, not limited to chord progression recognition. The implementation of NN uses Chainer, librosa for preprocessing, and mir_eval for calculating the correct answer rate.
Input preprocessing
The input of NN is the spectrum series (or spectrogram) of the music signal. If the procedure includes preprocessing,
- Separate the percussion instrument components of the music signal. Let's turn off the jamming percussion sounds. It is one shot with librosa.
- Constant-Q Transform. Speaking of spectrum transform, it is Fourier transform (STFT), but Fourier transform has the problem that "the frequency range is linear" and "the resolution is different for each frequency (because the window has a fixed length)". Since pitch information is important for music signals, it is desirable to display them in the logarithmic frequency range. It is possible to compress the FFT spectrum and convert it to the logarithmic frequency range, but here we use CQT, which changes the window length for each frequency so that the resolution does not change. ~~ Anyway, librosa is one shot. ~~ 24 dimensions for each octave (that is, 1/2 semitone for each dimension), and the spectrum for 6 octaves was calculated from the pitch of C0, so it is a 144-dimensional vector. The choice of numbers is rather appropriate.
- Logarithmic compression. Convert to f (X) = log (1 + X). This is a pre-processing that converts vector values into a logarithmic range to suppress noise. It seems to be a little robust.
- Concatenate adjacent vectors into a larger vector. For example, if there is a vector of time t, a total of 7 vectors from t-3 to t + 3 (padding if insufficient) are concatenated and converted into a 1008 (= 144x7) dimensional input vector. The input size also swells 7 times, but the recognition seems to be more stable. (* See also the supplement at the end of the sentence!) Now, let's throw this one-dimensional vector series (a set rather than a series for DNN) into DNN.
DNN-CRF model
Create an NN to learn the labeling of the spectrum series. It is a dimension that classifies each frame by DNN, sends it to CRF, takes into account the context of the label series, finds the plausibility of the series, and outputs the final label series. Let's write NN. Since the Chainer version uses CRF, there should be no problem if it is 1.13 or higher. Python is 2.7 series. Since we want to be able to easily control the number of hidden layers and the number of units, we use ChainList to define DNN. Well, it's just a normal stack of fully connected layers. The learning method is the same as the MNIST example, so no explanation is necessary.
dnn.py
class DNN(ChainList):
def __init__(self,links):
super(DNN,self).__init__(*links)
self.train = True
def __call__(self,x):
links = self.children()
h = x
for i in xrange(self.__len__()-1):
li = links.next()
h = F.dropout((F.relu(li(h))),train=self.train)
y = links.next()(h)#The final stage is a linear transformation
return y
And the definition of CRF. Chainer implements a model called linear-chain CRF, which seems to be popular in natural language processing, with only the previous label as the feature. Takes the output of DNN as input.
DNN.py
class CRF(Chain):
def __init__(self):
super(CRF,self).__init__(crf=L.CRF1d(N_CLASSES))
def __call__(self,list_x,list_t):
self.loss = self.crf(list_x,list_t)
return self.loss
def argmax(self,list_x):
~,path = self.crf.argmax(list_x)
return np.array(path,dtype="int32").flatten() #Since path is an array of batches, it is transformed
Looking at it again, there is almost no point in creating a new class ... Is that okay? When sending input to the CRF, you need to put the Variables together in an array (the documentation says list of Variables). When learning, you can speed up by batching. In my case, I wrote it as below. Y is the output of DNN calculated in advance, and it is an array of shape = (seqsize, 25) because it is all contained in one batch. T is the correct label series.
DNN.py
#Part of the learning loop
startidx = np.random.randint(0,seqsize-256-1,size=16*100)#Randomly determine the starting point of the series
for i in range(0,32*100,32):
x_batch_list = [Variable(cp.asarray(Y[startidx[i:i+32]+j,:])) for j in range(256)]
t_batch_list = [Variable(cp.asarray(T[startidx[i:i+32]+j])) for j in range(256)]
opt.update(crfmodel,x_batch_list,t_batch_list) #cp is cupy
In short, the flow is to randomly take 32 series of length 256 each time, combine them into one batch, and give them to the CRF. In the latest version, CRF1d seems to be able to handle series with different lengths in batch, but here it is fixed at 256 length. Easy to write. It is possible to put DNN and CRF in one chain and train them together, but here we divide it into two steps. First, use the training data to train only the DNN. The loss function is softmax_cross_entropy. After that, fix the DNN parameters and train the CRF. For label estimation, if you give a series of DNN output, CRF1d.argmax () will return the maximum likelihood route in the Viterbi search. Benly.
Label type
Let's go with the simplest MajMin rule. Ignoring Seventh, etc., in addition to 12 major triads and 12 minor triads, there are a total of 25 types, including a special label called No Chord (silence, single note, percuss only section, etc.).
Hyperparameters
DNN parameters are selected appropriately by referring to papers. --Optimization algorithm: AdaDelta --Number of input dimensions: 1008 (= 144x7) --Number of hidden layers: 4 --Number of hidden layer units: 512 --Dropout rate: 0.5 CRF optimization is also AdaDelta.
data set
The chord progression annotations published by isophonics.net are used for datasets. It is part of the entire Beatles album, Queen's best compilation album and the Kalore King album, and has a volume of about 200 songs. The notation of the annotation looks like this.
06_-_Let_It_Be.lab
0.000000 0.175157 N
0.175157 1.852358 C
1.852358 3.454535 G
3.434535 4.720022 A:min
...
...
If the recognition result by DNN is also output in this notation, the correct answer rate can be calculated by mir_eval and the recognition result can be visualized. The data set is randomly divided into train set and test set at about 5: 1. I don't do Cross validation because it's annoying. There is no validate set. Since it is a classification problem, the evaluation standard is correct answer rate = (sum of time when the estimated label answered correctly) / (sum of music length). After outputting the estimation result in the same text format as the isophonics dataset, I asked the mir_eval library to calculate the correct answer rate.
Performance evaluation
We measured the classification accuracy of the trained DNN test set and train set, and the final recognition accuracy in combination with the trained CRF.
| DNN(train set) | DNN(test set) | DNN-CRF(train set) | DNN-CRF(test set) |
|---|---|---|---|
| 77.0% | 68.4% | 84.7% | 76.6% |
You can see that the CRF greatly contributes to the accuracy of series labeling. It looks like this when Audacity visualizes the recognition result. This is a chord progression (part) of Here Comes The Sun of The Beatles. The bottom is the recognition result, and the top is the correct answer manually. I can't catch the small changes in the code, but I can see that it's mostly working.

Try to Residual
Let's remodel DNN like ResNet because it is a good idea. ResNet style modification by Chainer is super easy. Therefore Chainer is the strongest.
DNN.py
class DNNRes(ChainList):
def __init__(self,links):
super(DNNRes,self).__init__(*links)
self.train = True
def __call__(self,x):
links = self.children()
li = links.next()
h = F.relu(li(x)) #Do not convert from the input layer to Res
for i in xrange(self.__len__()-2):
li = links.next()
h = F.dropout(F.relu(li(h)),train=self.train)+h #here+Just add h
y = links.next()(h)
return y
It seems that the original ResNet has two hidden layers and one Residual Block, but ~~ It's annoying ~~ We give priority to comprehensibility and make each layer Residual. In the case of multiple layers, it is better to create a Residual Block in a separate class (Chain). The number of hidden layers has increased to 20. Since the overfitting was terrible, I added a slightly stronger Weight Decay in addition to Dropout. Coefficient 0.001.
result!
| DNN(train set) | DNN(test set) | DNN-CRF(train set) | DNN-CRF(test set) |
|---|---|---|---|
| 78.8% | 74.0% | 85.5% | 80.5% |
The accuracy of the test set has improved considerably. I went to 80% Odai.
Results of this year's MIREX is up to about 86%, so it's still a long way off, but I'm pretty good at it compared to others. (I can't compare exactly because it's not Cross validation).
About CRF implementation
For (linear-chain) CRF, see This article and [This article (English)](http://blog.echen.me/2012/01/ 03 / introduction-to-conditional-random-fields /) is recommended. CRF is
P(Y|X)=\frac{\exp{E(X,Y)}}{\sum_{Y'}{\exp{E(X,Y)}}}
The conditional probability of the label series Y is calculated like this (it becomes a loss function when multiplied by -log), but there are various definitions of the feature function E (X, Y). In the case of Chainer (guessed from the documentation),
E(X,Y)=\sum_i{(x_{iy_i}+c_{y_{i-1}y_i})}
And simply add the frame class loss x (calculated by DNN etc.) and the label transition cost c. In this case, the only parameter to be learned is the label transition cost matrix c.
Incorporating the upper DNN into this (assuming X is a spectral sequence),
E(X,Y)=\sum_i{(f_{dnn}(x_{iy_i})+c_{y_{i-1}y_i})}
It can be said that it was one big CRF as a whole in the first place. Or rather, the label transition cost is also non-linear,
E(X,Y)=\sum_i{(f_{dnn_1}(x_{iy_i})+f_{dnn_2}(c_{y_{i-1}y_i}))}
It may be an ant to do that. I feel like I'm gradually approaching RNNs. Looking at other papers,
E(X,Y)=\sum_i{(x_{iy_i}+c_{y_{i-1}y_i}+b_{y_i})}+\pi_{y_0}+\gamma_{y_N}
In this way, we see bias b and the potential (global features) at the beginning and end of the label series. Is this possible with a little tweaking of the Chainer implementation? When it comes to part-of-speech tagging tasks, it also seems to be a case-by-case function for suffixes (such as -ly). In this way, the fact that it is a discriminative model (directly obtains conditional probabilities), the feature function is flexible (global features and heuristic rules can be incorporated), and there are no restrictions on parameter values are often used in the same task. Difference from the HMM. Above all, if the parameters are differentiable, it can be learned by gradient descent, so it is compatible with NN! strongest! Therefore, it seems that the application is expanding in the task of series labeling. Chainer is also expected to have more variations in the future.
- Supplement: I plotted the matrix c in this example.
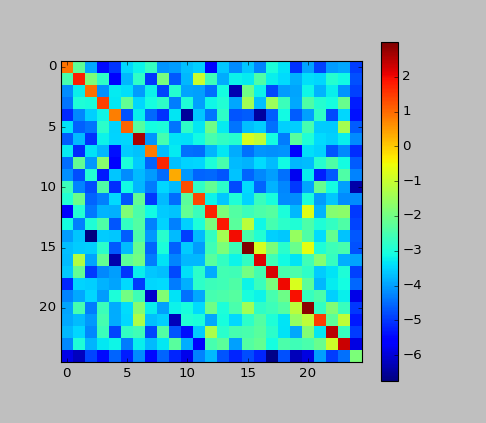 From the high value of the main diagonal, we can see that the CRF "works in the direction of suppressing the change of the label". It was almost like that in HMM.
From the high value of the main diagonal, we can see that the CRF "works in the direction of suppressing the change of the label". It was almost like that in HMM.
Summary
Please forgive me because the complete source code cannot be shown to anyone. I'm a research student on the subject of automatic ear copy, so I've introduced what I learned to some extent (also as a missionary in the MIR field). Formally, it's a really simple model for series labeling, but it still seems to perform quite well in the task of chord progression recognition. If you feel like it, you can make DNN deeper, make it CNN, or even make it RNN. I'm currently making a slightly more complicated model, but I'm writing a dissertation, so I hope I can introduce it again. I've been using Chainer for a long time, but it's really good. The feeling of being able to assemble as you envisioned is super comfortable and helpful. Therefore the strongest (second time).
Note: I forgot to normalize
I completely forgot to normalize the input in the pre-processing. What a mess. Start over. Put normalization between steps 3 (logarithmic conversion) and 4 of the preprocessing. I think there are various ways to do it, but here we will use global mean variance normalization (find the mean and var of the entire spectrogram for one song).
norm(X)=\frac{X-mean(X)}{var(X)}
Converted to a form that NN is pleased with, with an average value of 0 and a variance of 1.
I also reviewed the so-called logarithmic compression in step3. Originally, this process was a pre-process to compress the noise of the feature called Chromagram, which is often used in the same task, but since Chromagram is non-negative, it was necessary to maintain the property by adding +1 when performing logarithmic conversion. I used it for spectrogram preprocessing in another deep learning paper and imitated it, but when I think about it, it is not necessary to limit the input range to non-negative, so if so, +1 to compress the range It's a shame to do it. So you don't need +1.
f(X)=log(0.01+X)
If you write log normally, it's OK. 0.01 is for avoiding zero values. I tried this again with the Residual DNN-CRF settings.
| DNN(train set) | DNN(test set) | DNN-CRF(train set) | DNN-CRF(test set) |
|---|---|---|---|
| 84.8% | 77.4% | 88.6% | 82.0% |
It has grown a lot. After all pretreatment is important. Normalization is important. Let's all be careful!
Recommended Posts