Des robots aux voitures autonomes en passant par les jeux tels que Go et Shogi, de nombreuses «IA» deviennent populaires ces jours-ci.

L'un des mots clés est "renforcer l'apprentissage". En ce sens, il s'agit peut-être de la méthode la plus notable (et exagérée ...) de toutes les méthodes d'apprentissage automatique.

Cette fois, à propos de la méthode de renforcement de l'apprentissage, Deep Q-learning (soi-disant Dokyun, DQN, qui a récemment atteint une précision remarquable des bases. )), Je voudrais expliquer le flux et le mécanisme de son développement.

** Un événement pratique a été organisé sur la base du contenu de cet article (version améliorée et révisée de PyConJP Talk) **

Renforcer l'apprentissage en commençant par l'expérience pratique de Python OpenAI Gym

Les supports de cours sont plus riches en illustrations, c'est donc recommandé pour les formules et autres choses.

Caractéristiques de l'apprentissage par renforcement

L'apprentissage intensifié est similaire à l'apprentissage supervisé, mais ne fournit pas de «réponse» claire (par l'enseignant). Donc, ce qui est présenté, ce sont des «options d'action» et des «récompenses».

Si vous considérez cela comme la réponse = récompense, vous pouvez penser que c'est la même chose (action A = 10 pt, etc.), mais il y a une grande différence. Autrement dit, la récompense de l'apprentissage par renforcement n'est pas pour «chaque action» mais pour «le résultat d'actions continues». Dans le cas du football, un point pour un but est une récompense pour le renforcement de l'apprentissage. Cependant, aucune récompense n'est donnée pour chaque action de passe ou de dribble pour atteindre l'objectif. D'autre part, l'apprentissage instruit se produit lorsque des instructions sont envoyées de l'extérieur du court, disant: "La passe actuelle est bonne!" Et "Vous ne devriez pas dribbler là-bas!" Dans l'apprentissage par renforcement, un seul objectif en tant que «résultat d'une action continue» est récompensé, donc la qualité de la passe et du dribble pour l'atteindre dépend du cas où l'objectif a été atteint et du cas où cela n'a pas été possible. Vous devez faire vous-même l '«évaluation».

Alors, comment évaluez-vous chaque action? Tout d'abord, l'action au moment du but (le dernier tir) sera récompensée (1 point). Mais qu'en est-il de l'action juste avant cela? C'était aussi le réglage final pour marquer un but, donc je pense que c'était une très bonne décision. Ensuite, si vous calculez en arrière à partir de la précédente, vous pouvez évaluer chaque action rétroactivement à partir de la dernière action.

Dans l'apprentissage intensif, «l'évaluation» de chaque action est mise à jour par soi-même à partir de la récompense du «résultat d'actions continues» de cette manière. De cette façon, même si vous ne définissez pas une récompense pour chaque action une par une, vous apprendrez des actions continues qui obtiendront finalement une récompense basée sur votre propre évaluation. Dans le cas de jeux compliqués tels que le shogi et le go, il peut être difficile de décider quel coup est le meilleur dans quelle situation, et encore moins combien de points la récompense devrait être. Même dans de tels cas, la victoire ou la perte finale est claire, vous pouvez donc appliquer un apprentissage par renforcement pour éviter la difficulté de l'évaluation comportementale et apprendre le comportement gagnant final. En conséquence, un apprentissage amélioré peut gérer des problèmes plus complexes en général que l'apprentissage supervisé.

Cependant, veuillez noter que cela ne signifie pas que l'apprentissage amélioré est une meilleure méthode que l'apprentissage supervisé. Pour le dire autrement, renforcer l'apprentissage prend beaucoup de temps car il faut acquérir en soi une «évaluation du comportement» sans instructions claires. Le nombre d'actions pour atteindre l'objectif, et le nombre de combinaisons de celles-ci, est énorme et l'optimisation prend beaucoup de temps (bien que les ordinateurs soient rapides en calcul). En outre, il n'y a aucune garantie raisonnable du point de vue humain que «l'évaluation du comportement» acquise en renforçant l'apprentissage le soit. Il est clair qu'il y a un bon enseignant et que le premier est plus efficace et plus facile à trouver la solution optimale si vous étudiez par vous-même, vous devez donc choisir la méthode d'apprentissage de manière appropriée en fonction du problème que vous rencontrez.

Ce qui précède sont les caractéristiques d'un apprentissage amélioré. Ensuite, je vais modéliser cela et expliquer comment l'apprendre.

Modélisation de l'apprentissage par renforcement (processus décisionnel de Markov)

Le problème ciblé par l'apprentissage intensif est modélisé comme suit.

States: S
Statut. Dans le jeu, cela représente un aspect spécifique
Model: T(s, a, s') (=P(s'|s, a))
T est Transition, et si vous agissez dans la situation s, vous serez dans la situation s '. Cependant, c'est une expression probabiliste (P (s 's, a)) car elle exprime une situation où même si a est sélectionné, elle ne s'active pas ou va à un autre endroit.
Actions: A(s), A
Action. Si l'action qui peut être entreprise change en fonction de la situation, elle devient une fonction telle que A (s)
Reward: R(s), R(s, a), R(s, a , s')
Situations et récompenses des actions dans ces situations. Cette récompense est auto-évaluée à l'exception du résultat final (récompense immédiate).
Policy: \pi(s) -> a
Stratégie. Une fonction qui renvoie quelle action a doit être entreprise dans la situation s.

Cette modélisation est appelée le processus de décision de Markov (MDP, processus de décision de Markov). Markov signifie la nature de Markov, ce qui signifie que seul le ou les états actuels sont impliqués dans l'action suivante, représentée par $ \ pi (s) $.

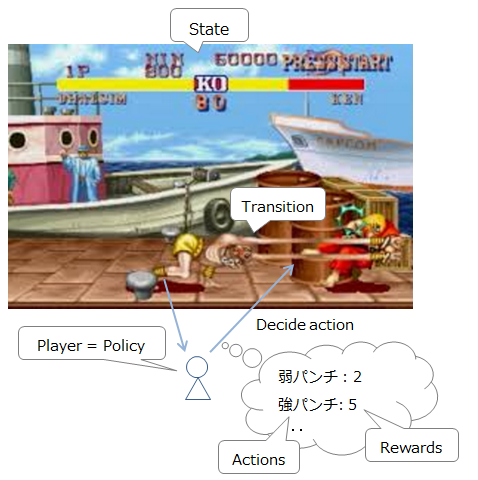
Pour l'expliquer en tant que combattant de rue, cela ressemble à ce qui suit.

Situation actuelle (position ennemie / propre et HP): état
Commandes actuellement disponibles: Actions
Mouvement / attaque etc: T (s, a, s ') Liste des commandes qui peuvent être entrées et leurs probabilités d'activation (car vous pouvez manquer une commande même si vous essayez d'émettre un feu de yoga, cela devient probabiliste)
Joueur (personne décisionnaire): Politique
Récompense pour l'action: récompense
De plus, j'ai reçu un commentaire disant: "Je voulais que vous fassiez le guerrier le plus puissant de Strike 2 par apprentissage automatique", mais la capacité de combat de l'IA a déjà dépassé celle des gens ordinaires, et au contraire, "comment régler" est un problème (Référence). L'humanité doit travailler dur pour s'entraîner.

Au fait, dans un combat de rue, raser les PV de l'adversaire est le chemin le plus court pour gagner, mais il est clair qu'il est difficile de gagner à la fin même avec juste des coups de poing. Par conséquent, afin d'optimiser la stratégie, il est nécessaire de maximiser la récompense à long terme, pas à court terme.

Cependant, si le temps est infini même pour une longue période de temps, le zoom punching (voir la figure ci-dessus) est la stratégie la plus efficace d'aussi loin que possible. En effet, si vous avez un temps infini, il est plus sûr de prendre des mesures qui au moins se tiennent à l'écart de l'adversaire, plutôt que de risquer de s'approcher et de faire des flammes de yoga. De cette façon, lorsque le temps est infini, il a tendance à être biaisé vers un comportement à faible risque et à faible rendement, nous allons donc introduire le concept de remise par le temps. En d'autres termes, si vous n'agissez pas rapidement, vous obtiendrez de moins en moins de récompense pour la même action.

En d'autres termes, les deux points suivants sont importants pour optimiser la stratégie.

Essayez d'optimiser la somme des récompenses
Introduisez une remise de récompense au fil du temps

Cela peut être exprimé comme une expression comme suit.

U^{\pi}(s) = E \left[ \sum_{t}^{\infty} \gamma^{t} R(s_t) | \pi, s_0=s \right]

Somme des récompenses = $ U ^ {\ pi} (s) $: Somme des récompenses lors de l'exécution de la stratégie $ \ pi $ à partir de l'état $ s $ ($ \ pi, s_0 = s $)
Remise à temps = $ \ gamma $: $ 0 \ leq \ gamma <1 $, une valeur proche de 1

Le but est de découvrir une stratégie qui maximise cette «somme de récompenses compte tenu des réductions de temps». Appelons cette stratégie optimale $ \ pi ^ * $. Dans la meilleure stratégie, vous devez essentiellement agir pour maximiser votre récompense. Cela peut être exprimé mathématiquement comme suit.

\pi^{*}(s) = argmax_a \sum_{s'} T(s, a, s') U(s')

$ argmax $ signifie choisir le plus grand. En d'autres termes, sur $ s '$, qui est la destination de transition à partir de $ s $, la récompense totale attendue $ U (s') $ agira vers le maximum $ s '$. Après tout, la stratégie optimale $ \ pi ^ * $ signifie que tout $ s $ se comportera de telle manière que la somme des récompenses qui en découle soit maximisée, donc le premier défini $ U ^ {\ Vous pouvez réécrire pi} (s) $ comme suit:

U(s) = R(s) + \gamma max \sum_{s'} T(s, a, s') U(s')

Cette équation est appelée ** équation de Bellman **. La raison pour laquelle je l'ai réécrit de cette façon est que j'ai pu extraire la stratégie $ \ pi $ de la formule afin que je puisse «calculer sa récompense quelle que soit la stratégie que j'ai choisie». En d'autres termes, le comportement optimal ne peut être calculé qu'à partir des paramètres du jeu (environnement). C'est l'élément clé pour la formation du modèle.

Apprentissage de modèle

De là, je vais vous expliquer comment entraîner le modèle construit ci-dessus.

Value Iteration

En utilisant l'équation de Bellman dérivée précédemment, calculons immédiatement le comportement optimal "à partir de l'environnement uniquement". Dans ce calcul, comme expliqué dans la première section, le calcul est répété à partir de l'état où la "dernière récompense" a été obtenue. Ce calcul itératif est appelé ** Itération de valeur **.

Ci-dessous, l'état de l'itération de valeur est illustré à l'aide de l'exemple de Pacman.

Il est calqué sur Markov Decision Processes and Reinforcement Learning, p18 ~ 21.

Si vous notez cette situation, ce sera comme suit.

Définir une récompense fixe
Pour chaque état, calculez les récompenses gagnées par un

\gamma \sum T(s, a, s') U(s')

Calculez la récompense totale $ U (s) $ en a, ce qui donne la récompense la plus élevée en 1.

U(s) = R(s) + \gamma max \sum_{s'} T(s, a, s') U(s') = Bellman Equation!

Revenez à 1 jusqu'à ce qu'il converge (jusqu'à ce que la largeur de mise à jour de $ U (s) $ devienne plus petite) et répétez la mise à jour.

Il a été prouvé qu'il finira par converger vers la valeur attendue.

De cette manière, Value Iteration a pu estimer la carte de récompense "à partir de l'environnement uniquement". Cependant, dans cet état, toutes les actions qui peuvent être placées dans toutes les situations sont minutieusement étudiées, de sorte que l'action optimale peut être dérivée, mais elle n'est pas très efficace. Par conséquent, nous déciderons d'abord d'une stratégie appropriée, puis rechercherons des récompenses dans cette fourchette et envisagerons une méthode de mise à jour. C'est une itération de politique.

Policy Iteration

Dans Policy Itteration, décidez d'abord d'une stratégie (aléatoire) appropriée $ \ pi_0 $. Ensuite, vous pouvez calculer la "récompense de la stratégie" $ U ^ {\ pi_0} (s) , et améliorer la stratégie en fonction de celle-ci ( \ pi_1 $). En d'autres termes, les étapes sont les suivantes.

Décidez d'une stratégie appropriée ($ \ pi_0 $)
Calculez $ U ^ {\ pi_t} (s) $ en fonction de la stratégie
Mettez à jour la stratégie $ \ pi_t $ en $ \ pi_ {t + 1} . ( \ pi_ {t + 1} = argmax_a \ somme T (s, a, s ') U ^ {\ pi_t} (s') $)
Revenez à 1 jusqu'à ce qu'il converge et répétez la mise à jour

La convergence signifie $ \ pi_ {t + 1} \ approx \ pi_ {t} $, c'est-à-dire lorsque l'action sélectionnée est presque inchangée. Cette répétition est appelée ** Itération de politique **.

Maintenant, il semble possible de calculer la stratégie optimale en utilisant l'itération de valeur et l'itération de politique. Cependant, comme vous pouvez le voir à partir de la formule, ce calcul nécessite que $ T (s, a, s ') $ soit connu. En d'autres termes, il est nécessaire de clarifier à l'avance la destination de transition lorsque l'on agit dans chaque situation. C'est une contrainte délicatement grande, et surtout quand il y a un grand nombre de situations et d'actions qui peuvent être prises, il est très difficile de tout définir comme "C'est ce qui se passe ici ...".

Le Q-learning, qui sera présenté dans la section suivante, résout ce problème. Elle est également appelée méthode d'apprentissage «sans modèle» car elle ne nécessite pas de paramètres d'environnement (modèle) préalables.

Q-learning

Alors, comment apprendre en Q-learning sans informations sur l'environnement (modèle)? La réponse est «essayez d'abord». Même si $ T (s, a, s ') $ est inconnu, si vous effectuez une action a dans l'état s une fois, cela deviendra clair, vous apprendrez donc en répétant cet "essai". .. Bien sûr, cela prend beaucoup de temps pour faire une telle chose, donc dans ce sens, il y a un avantage qu'il n'est pas nécessaire de définir le modèle à l'avance, mais d'un autre côté, c'est un handicap en termes de temps d'apprentissage.

La formule pour «essayer d'abord» est la suivante.

Q(s, a) \approx R(s, a) + \gamma max_{a'} E[Q(s', a')]

$ T (s, a, s ') $ a disparu et est maintenant la valeur attendue ($ E [Q (s', a ')] ). Cette valeur attendue sera affinée en répétant l'essai. Par conséquent, à la fin, les expressions qui sont presque égales ( \ approx ) ci-dessus seront établies comme des expressions égales. Parce que, le fait que l'équation soit vraie signifie que la valeur attendue ( Q (s, a) ) et la valeur attendue lorsqu'elle agit réellement ( R (s, a) + \ gamma max_ {a '} E [ C'est parce que Q (s ', a')] $) est égal, ce qui signifie que nous avons une estimation précise de la récompense. Ceci est un guide pour terminer l'apprentissage.

La formule de ce processus d'apprentissage est la suivante.

Q(s, a) = Q(s, a) + \alpha(\underline{R(s, a) + \gamma max_{a'} E[Q(s', a')]} - \underline{Q(s, a)})

$ \ Alpha $ est le taux d'apprentissage, ce qui signifie que vous apprendrez de la différence entre la valeur attendue ($ \ approx $ récompense réelle) et la valeur attendue. Cette différence (= erreur) est appelée erreur TD (TD = différence temporelle), et la méthode d'apprentissage basée sur l'erreur TD est appelée apprentissage TD. En d'autres termes, le Q-learning est une sorte d'apprentissage TD.

La formule ci-dessus est également appliquée comme suit.

Q(s, a) = (1 - \alpha)\underline{Q(s, a)} + \alpha(\underline{R(s, a) + \gamma max_{a'} E[Q(s', a')]})

Ça devient un peu compliqué, mais au final, on essaie de clarifier "quel type d'état, comment agir et quel genre de récompense". Le tableau des perspectives de cette récompense est appelé le Q-Table (voir la figure ci-dessous).

Markov Decision Processes and Reinforcement Learning, p39

De la p39 à la p46 du matériel ci-dessus, vous pouvez vérifier comment le Q-Table est mis à jour, c'est-à-dire comment l'apprentissage progresse, veuillez donc vous y référer (0.9 dans le matériel est $). \ gamma $, le taux d'actualisation de la récompense).

Maintenant, nous pouvons améliorer $ Q (s, a) $ de plus en plus ... mais il reste la question de savoir comment décider a en premier lieu. En bref, vous devriez choisir celui avec le plus grand $ Q (s, a) $, mais si vous faites cela, vous continuerez à sélectionner le "maximum connu", donc la récompense est toujours inconnue. Cela réduira les chances d'atteindre le niveau le plus élevé. Empruntez un chemin inconnu où il peut y avoir des trésors, ou un chemin stable avec des récompenses connues ... Ceci est un compromis et s'appelle le dilemme de l'exploration et de l'exploitation. Je vais.

Il existe plusieurs approches à ce problème, mais la méthode de base est la méthode ε-gourmande. C'est une méthode d'aventure avec une probabilité de ε, puis avide, c'est-à-dire agissant sur la base de récompenses connues. Une autre distribution de Boltzmann ($ P (a | s) = \ frac {e ^ {\ frac {Q (s, a)} {k}}} {\ sum_j e ^ {\ frac {Q (s, a_j)) Il existe une méthode utilisant} {k}}} $), qui est aléatoire lorsque $ k $ est grand, et à mesure qu'il devient plus petit, il devient connu pour prendre des actions très gratifiantes.

Il a été prouvé que si vous répétez l'action basée sur la stratégie et mettez à jour $ Q (s, a) $, elle finira par converger vers la valeur optimale. Oui un jour ... Cependant, comme ce sont les êtres humains qui ne peuvent pas attendre un jour, diverses tentatives ont été faites pour trouver comment se rapprocher des $ Q (s, a) $ optimaux. Parmi eux, l'approximation utilisant le réseau de neurones a conduit au DQN et au Deep Q-learning, qui ont atteint une précision remarquable ces dernières années.

Deep Q-learning

La base de l'apprentissage d'un réseau neuronal est la méthode de propagation d'erreur (Back Propagation). En bref, c'est une méthode d'ajustement du modèle pour qu'il soit proche de la bonne réponse en calculant l'erreur à partir de la bonne réponse et en la propageant dans la direction opposée.

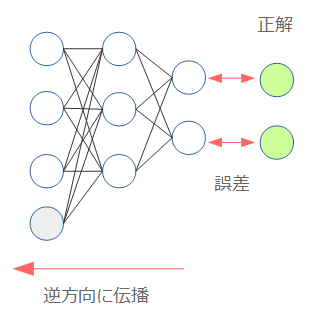Réseau neuronal commençant par Chainer

Par conséquent, la question est de savoir quelle est «l'erreur» lors de l'approximation de $ Q (s, a) $ avec un réseau neuronal. Ici, une erreur appelée "erreur TD" est apparue ci-dessus.

Q(s, a) = Q(s, a) + \alpha(R(s, a) + \gamma max_{a'} E[Q(s', a')] - Q(s, a))

C'était la différence entre la récompense attendue ($ \ approx $ récompense réelle) et la perspective. C'est probablement le point de départ de la définition de l'erreur. Tout d'abord, le réseau neuronal $ Q (s, a) $. Le poids du réseau neuronal à ce moment est $ \ theta $ et $ Q_ \ theta (s, a) $. Ensuite, la définition de l'erreur utilisant l'erreur TD dans la formule ci-dessus est multipliée comme suit.

L_\theta = E[\frac{1}{2} (\underline{R(s, a) + \gamma max_{a'} Q_{\theta_{i-1}}(s', a')} - Q_\theta(s, a))^2]

Le carré est dû à l'erreur, et le $ \ frac {1} {2} $ consiste à éliminer le 2 qui apparaît lors de la différenciation ($ f (x) = x ^ 2 $). Lorsque $ f '(x) = 2x $). Comme vous pouvez le voir dans la structure de la formule, la partie soulignée (valeur attendue) est le libellé de l'enseignant (cible) dans l'apprentissage supervisé. Ensuite, le gradient au moment de la propagation d'erreur obtenu en différenciant cette équation est le suivant.

\nabla_\theta L(\theta_i) = E[(\underline{R(s, a) + \gamma max Q_{\theta_{i-1}}(s', a')} - Q_{\theta_i}(s, a))\nabla_\theta Q_{\theta_i}(s, a)]

Maintenant, vous êtes prêt à partir. Cependant, qui a une bonne compréhension? Vous pourriez penser, mais $ Q $ du côté de la valeur attendue est $ Q_ {\ theta_ {i-1}} (s ', a') $. En effet, la valeur attendue est calculée à l'aide du $ \ theta $ précédent. Comme mentionné ci-dessus, cela sert d'étiquette d'enseignant dans l'apprentissage supervisé, donc $ \ theta $ est inclus dans la formule du côté de la valeur attendue, mais ce n'est pas une cible différentielle lors du calcul du gradient. Cela doit être gardé à l'esprit lors de la mise en œuvre.

Maintenant, tout ce que vous avez à faire est d'apprendre ... mais en réalité, apprendre tel qu'il est ne fonctionne pas très bien. Il est naturel que le nombre de paramètres ait augmenté en raison du filet neuronal. Par conséquent, une certaine ingéniosité dans l'apprentissage a été mise au point, et le Deep Q-learning n'est possible que lorsqu'il est inclus.

Experience Replay

Les données fournies dans l'apprentissage par renforcement sont, bien entendu, continues par ordre chronologique. Si tel est le cas, il y aura une corrélation entre les données, le but d'Expérience Replay est donc de les séparer.

La méthode consiste à stocker d'abord l'état / l'action / la récompense / la destination de transition expérimentés dans la mémoire, puis à échantillonner au hasard et à l'utiliser lors de l'apprentissage.

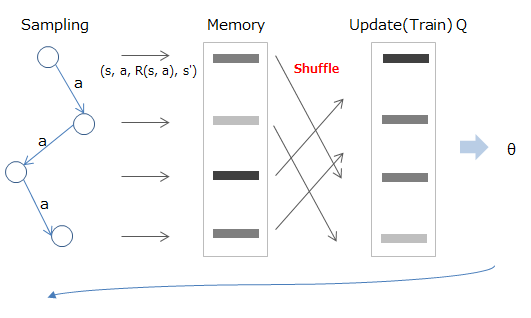
Mathématiquement, c'est comme échantillonner à partir de la valeur stockée dans la mémoire (D) comme indiqué ci-dessous (partie rouge) et apprendre en utilisant la valeur attendue calculée (partie bleue).

Deep Reinforcement Learning/David Silver, Google DeepMind, p12

Fixed Target Q-Network

$ Q_ {\ theta_ {i-1}} (s ', a') $ inclus dans la valeur attendue, qui est le poids précédent $ \ theta_ {i, même s'il agit comme une étiquette d'enseignant. Cela dépend de -1} $. Par conséquent, l'étiquette change en tant que B, et $ \ theta $ est mis à jour, même si c'était A il y a quelque temps. C'est un état de changement le matin.

Par conséquent, comme dans Experience Replay ci-dessus, extrayez d'abord quelques échantillons des données pour créer un mini-lot, et pendant la formation, le $ \ theta $ utilisé pour calculer la valeur attendue est fixe.

Mathématiquement, en corrigeant $ w ^ - $ (rouge) utilisé pour calculer la valeur attendue comme indiqué ci-dessous, la valeur attendue (partie bleue) est stabilisée. Une fois l'apprentissage terminé, mettez à jour $ w ^ - $ en $ w $ et passez au calcul du lot suivant.

Deep Reinforcement Learning/David Silver, Google DeepMind, p13

Coupure de récompense

Cela signifie que la récompense à donner est fixe, donc si elle est positive, elle sera de 1 et si elle est négative, elle sera de -1. Par conséquent, il n'est pas possible de pondérer la récompense (comme 10 points! Parce que j'ai pu atteindre l'objectif rapidement), mais au contraire, il devient plus facile de procéder à l'apprentissage.

Comme décrit ci-dessus, le Deep Q-learning comprend le procédé d'approximation du Q-learning avec un réseau neuronal et (au moins) les trois techniques ci-dessus pour un apprentissage efficace dans ce cas. L'approximation de réseau neuronal présente également l'avantage qu'un vecteur numérique peut maintenant être reçu comme entrée pour l'état s. Dans des jeux tels que la rupture de bloc, cela permet d'effectuer des astuces telles que la vectorisation de l'écran de jeu tel qu'il est et sa saisie et son apprentissage, et AlphaGo utilise également la même méthode (en utilisant l'image du plateau telle qu'elle est en entrée). ..

Le Deep Q-learning fait actuellement l'objet de diverses améliorations, mais je pense que la compréhension du contenu ci-dessus vous aidera à comprendre lorsque vous suivrez les tendances de la recherche.

Entraine toi

Jusque-là, le contenu était théorique, alors essayons-le à partir d'ici. Il existe une plate-forme appelée Open AI qui résume divers environnements d'apprentissage pour un apprentissage amélioré. Cette fois, je vais l'utiliser pour apprendre réellement l'algorithme.

OpenAI Gym OpenAI ouvre un "gym d'entraînement pour l'IA"

Comme vous pouvez le voir ici, divers environnements d'apprentissage tels que des jeux sont fournis. C'est amusant de le regarder.

OpenAI Gym environments

Il s'agit en fait d'une bibliothèque Python, et la méthode d'installation est décrite en détail sur le GitHub officiel.

openai/gym

L'installation est essentiellement pip install gym, mais cela ne peut être exécuté que dans l'environnement suivant avec l'installation de configuration minimale.

algorithmic
toy_text
classic_control (nécessite pyglet pour dessiner)

D'autres environnements d'apprentissage nécessitent une installation supplémentaire. Par exemple, si vous voulez exécuter des jeux Atari, vous devez installer des modules supplémentaires avec pip install gym [atari]. Vous devrez peut-être installer autre chose que Python, il est donc sûr d'inclure ceux répertoriés dans Tout installer. Lors de l'utilisation avec Python3, veuillez noter la description de Supported-systems.

L'utilisation est celle décrite dans Document, mais elle ressemble à ce qui suit.

import gym


env = gym.make('CartPole-v0')  # make your environment!

for i_episode in range(20):
    observation = env.reset()
    for t in range(100):
        env.render()  # render game screen
        action = env.action_space.sample()  # this is random action. replace here to your algorithm!
        observation, reward, done, info = env.step(action)  # get reward and next scene
        if done:
            print("Episode finished after {} timesteps".format(t+1))
            break

Initialisez l'environnement avec ʻenv.reset () `(équivalent à réinitialiser le jeu)
À partir de l'état observé (état = ʻobservation`), déterminez l'action par un algorithme
Obtenez la récompense pour l'action et le prochain état de transition par l'action par "env.step (action) "
done indique la fin de l'épisode (avec le résultat du jeu). Lorsque vous atteignez ce point, revenez à 1 et recommencez à apprendre.

Avec ʻenv.monitor`, vous pouvez facilement surveiller la précision et prendre des vidéos. Ce résultat peut également être téléchargé sur le site OpenAI, donc si vous êtes celui-là, essayez-le.

Voici le code que j'ai réellement implémenté. Puisque les résultats sont téléchargés sur OpenAI Gym, vous pouvez également y consulter les résultats de l'évaluation (algorithme d'icoxfog417).

icoxfog417/chainer_pong

Lors de la mise en œuvre, j'ai fait référence au code suivant.

Cela prend beaucoup de temps à apprendre, donc il faut beaucoup de temps pour déterminer si cela fonctionne (le code essentiel ci-dessus prend environ 3 jours à apprendre). Comme pour la reconnaissance d'image, en bref, le développement est difficile sans GPU. En ce sens, les GPU deviennent indispensables dans l'apprentissage automatique moderne s'il ne s'agit pas seulement d'exécuter des échantillons.

Cependant, il devient plus facile de préparer un environnement tel qu'une instance GPU d'AWS, alors essayez-le (même si ce sera très excitant lors du lancement d'une instance).

C'est tout pour l'explication. J'espère que vous pourrez plonger de zéro à profond!

Apprentissage amélioré pour apprendre de zéro à profond

Caractéristiques de l'apprentissage par renforcement

Modélisation de l'apprentissage par renforcement (processus décisionnel de Markov)

Apprentissage de modèle

Coupure de récompense

Entraine toi

Les références