L'apprentissage en profondeur

Deep Learing

perceptron

Contexte

Ce programme a été conçu en 1957 par un chercheur nommé Rosenblatt des États-Unis. Perceptron est à l'origine du réseau neuronal.

Qu'est-ce que Perceptron?

Il reçoit plusieurs signaux en tant qu'entrées et sort un signal. Le signal de Perceptron est "1 ou 0". Le Perceptron qui reçoit les deux signaux comme entrées est le suivant.

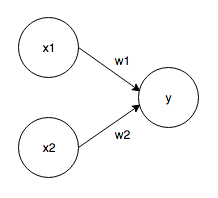
Signal d'entrée: x1, x2 Signal de sortie: y Poids: w1, w2 Lorsque le signal d'entrée est envoyé au neurone, chacun est multiplié par un poids unique, et 1 n'est émis que lorsque la somme dépasse la valeur limite (seuil, θ).

f(x) = \left\{
\begin{array}{ll}
0 & (w1x1 + w2x2 \leq θ) \\
1 & (w1x1 + w2x2 \gt θ)
\end{array}
\right.

Implémentation de Perceptron

Prenant la porte ET comme exemple ...

def AND(x1,x2):
    w1,w2,theta = 0.5,0.5,0.7
    tmp = x1*w1 + x2*w2
    if tmp <= theta:
        return 0
    elif tmp > theta:
        return 1

Introduire le biais

Transformez l'équation ci-dessus avec θ en -b

f(x) = \left\{
\begin{array}{ll}
0 & (b + w1x1 + w2x2 \leq 0) \\
1 & (b + w1x1 + w2x2 \gt 0)
\end{array}
\right.

La porte ET ressemble à ceci

import numpy as np
def AND(x1,x2):
    x = np.array([x1,x2])
    w = np.array([0.5,0.5])
    b = -0.7
    tmp = np.sum(w*x) + b
    if tmp <= 0:
        return 0
    else:
        return 1

La porte NAND ressemble à ceci

import numpy as np
def AND(x1,x2):
    x = np.array([x1,x2])
    w = np.array([-0.5,-0.5])
    b = 0.7
    tmp = np.sum(w*x) + b
    if tmp <= 0:
        return 0
    else:
        return 1

La porte OU ressemble à ceci

import numpy as np
def AND(x1, x2):
    x = np.array([x1, x2])
    w = np.array([0.5, 0.5])
    b = -0.2
    tmp = np.sum(w * x) + b
    if tmp <= 0:
        return 0
    else:
        return 1

Différence de travail

Poids => Contrôler l'importance du signal d'entrée Bias => Contrôle la facilité d'allumage

Les limites de Perceptron

Percepton ne peut pas représenter les portes XOR. Cependant, il peut être exprimé par des ** couches d'empilement **.

def XOR(x1,x2):
    s1 = NAND(x1,x2)
    s2 = OR(x1,x2)
    y = AND(s1,s2)
    return y

réseau neuronal

Il a la propriété que les paramètres de poids appropriés peuvent être automatiquement appris à partir des données.

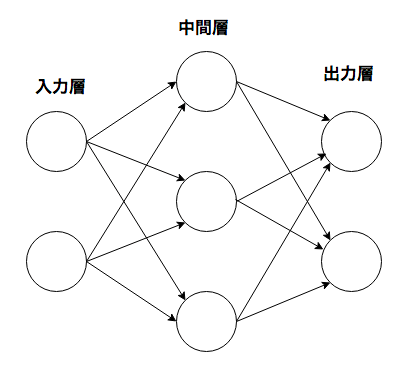
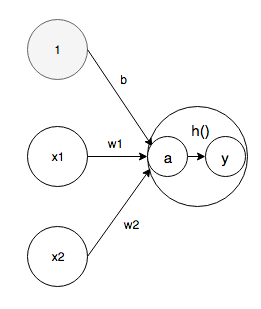
Fonction d'activation

La fonction d'activation est une fonction qui convertit la somme des signaux d'entrée en signaux de sortie. Dans un réseau de neurones, il est nécessaire d'utiliser une fonction non linéaire.

a = b + w1x1 + w2x2 \\
y = h(a)

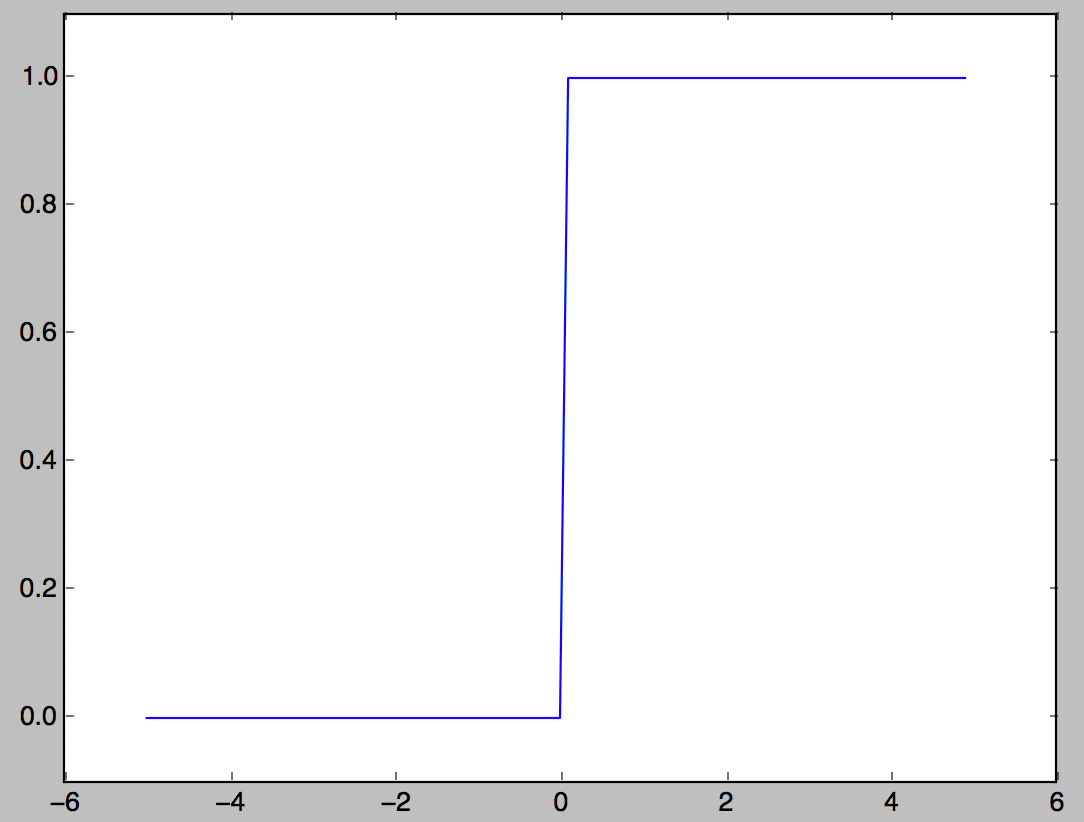
Fonction Step

L'une des fonctions d'activation qui produit 1 lorsque l'entrée dépasse 0 et 0 sinon.

import numpy as np
import matplotlib.pylab as plt
def step_function(x):
    y = x > 0
    return y.astype(np.int)

x = np.arange(-5.0,5.0,0.1)
y = step_function(x)
plt.plot(x,y)
plt.ylim(-0.1,1.1)
plt.show()

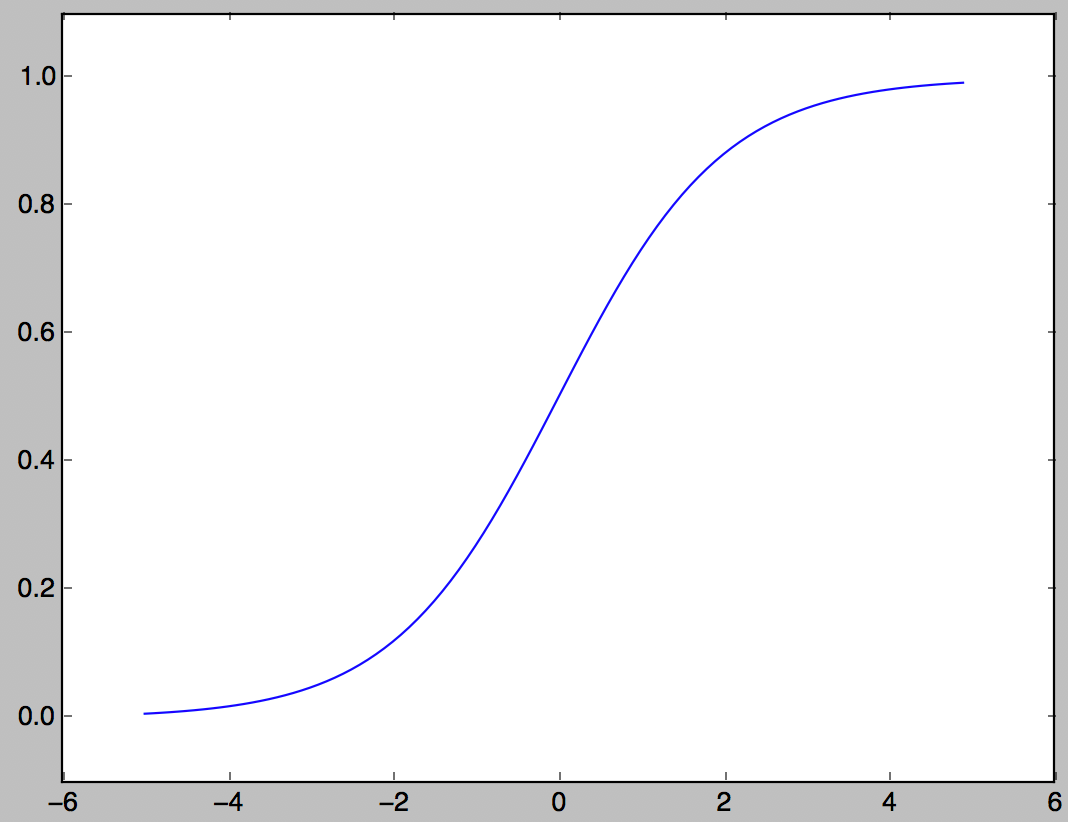
Fonction Sigmaid

L'une des fonctions d'activation souvent utilisées dans les réseaux de neurones.

h(x) = \frac{1}{1+e^{-x}}

import numpy as np
import matplotlib.pylab as plt
def sigmoid(x):
    return 1/(1+np.exp(-x))

x = np.arange(-5.0,5.0,0.1)
y = sigmoid(x)
plt.plot(x,y)
plt.ylim(-0.1,1.1)
plt.show()

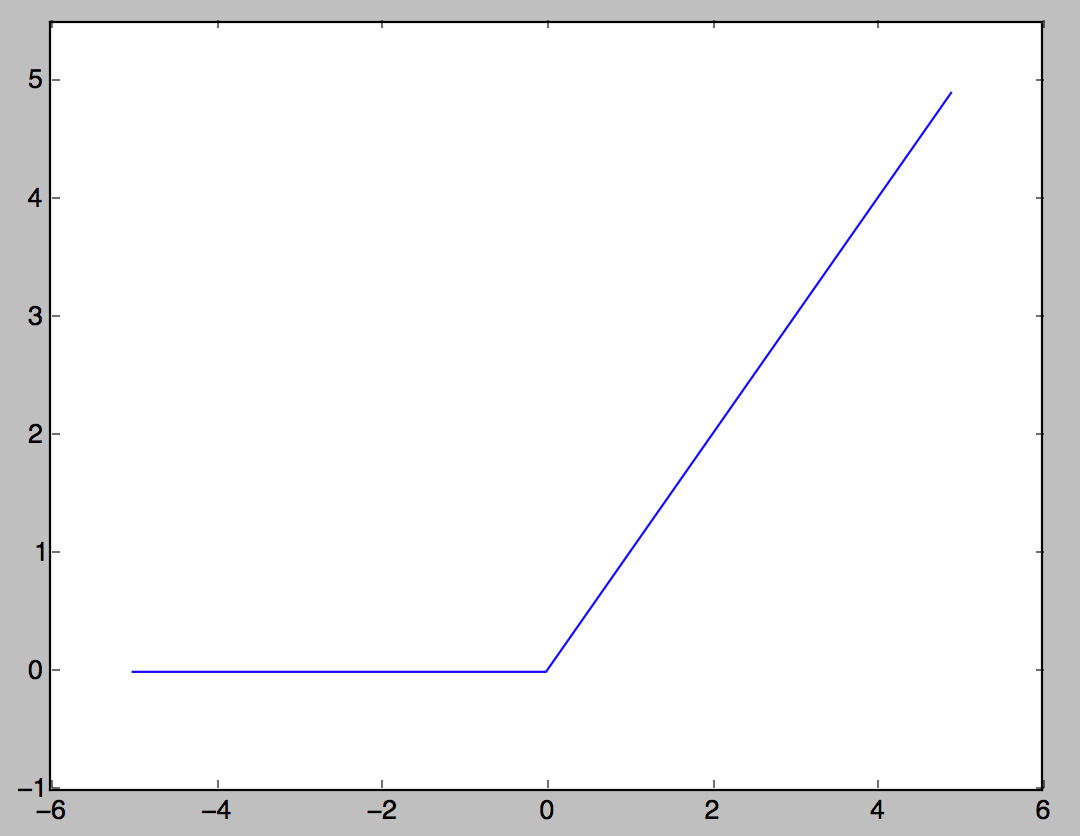
Fonction ReLU

Fonction d'activation souvent utilisée de nos jours. Si l'entrée dépasse 0, l'entrée est sortie telle quelle, et si elle est égale ou inférieure à 0, 0 est sortie.

h(x) = \left\{
\begin{array}{ll}
x & (x \gt 0) \\
0 & (x \leq 0)
\end{array}
\right.

import numpy as np
import matplotlib.pylab as plt
def relu(x):
    return np.maximum(0, x)

x = np.arange(-5.0,5.0,0.1)
y = relu(x)
plt.plot(x,y)
plt.ylim(-1.0,5.5)
plt.show()

Implémentation d'un réseau neuronal à 3 couches

#Définir un nombre
def init_network():
    network = {}
    network['W1'] = np.array([[0.1, 0.3, 0.5], [0.2, 0.4, 0.6]])
    network['b1'] = np.array([0.1, 0.2, 0.3])
    network['W2'] = np.array([[0.1, 0.4], [0.2, 0.5], [0.3, 0.6]])
    network['b2'] = np.array([0.1, 0.2])
    network['W3'] = np.array([[0.1, 0.3], [0.2, 0.4]])
    network['b3'] = np.array([0.1, 0.2])

    return network

#Fonction pour calculer jusqu'à la couche de sortie
def forward(network, x):
    W1, W2, W3 = network['W1'], network['W2'], network['W3']
    b1, b2, b3 = network['b1'], network['b2'], network['b3']

    a1 = np.dot(x, W1) + b1
    z1 = sigmoid(a1)
    a2 = np.dot(z1, W2) + b2
    z2 = sigmoid(a2)
    a3 = np.dot(z2, W3) + b3
    y = identity_function(a3)

    return y

#la mise en oeuvre
network = init_network()
x = np.array([1.0, 0.5])
y = forward(network, x)

Fonction Softmax

Fonctions souvent utilisées dans les problèmes de classification

y_k = \frac{e^{a_k}}{\sum_{i = 1}^{n}e^{a_i}}

Des mesures de débordement sont nécessaires pour calculer la fonction exponentielle

\begin{align}
y_k & = \frac{Ce^{a_k}}{C\sum_{i = 1}^{n}e^{a_i}} \\
& =  \frac{e^{a_k+\log C}}{\sum_{i = 1}^{n}e^{a_i+\log C}} \\
& =  \frac{e^{a_k+C'}}{\sum_{i = 1}^{n}e^{a_i+C'}} \\
\end{align}

Il est courant d'utiliser la valeur maximale du signal d'entrée pour C '.

import numpy as np
def softmax(a):
    c = np.max(a)
    exp_a = np.exp(a - c)
    sum_exp_a = np.sum(exp_a)
    y = exp_a/sum_exp_a
    return y

Apprentissage du réseau neuronal

Apprentissage = obtenir automatiquement la valeur optimale du paramètre de poids à partir des données d'entraînement Introduisez une fonction de perte pour permettre au réseau de neurones de s'entraîner. Objectif: trouver le paramètre de pondération qui minimise sa valeur par rapport à la fonction de perte La ** méthode du gradient ** est utilisée pour atteindre cet objectif.

Axé sur les données

Considérons un programme qui reconnaît le nombre «5». Il est très difficile de créer un programme qui reconnaît «5» à partir de zéro, alors utilisez efficacement les données. Il existe une méthode pour extraire des ** caractéristiques ** de l'image et apprendre le modèle des caractéristiques à l'aide de la technologie d'apprentissage automatique. Fonctionnalité = Convertisseur conçu pour extraire avec précision les données essentielles (données importantes) des données d'entrée (image d'entrée) Dans le réseau neuronal, la "machine" apprend même les caractéristiques contenues dans l'image.

Fonction de perte

Un indicateur de la mesure dans laquelle le réseau neuronal ne correspond pas aux données de l'enseignant (plus petit est moins d'erreur) Généralement, il existe une erreur de somme des carrés, une erreur d'entropie croisée, etc.

Erreur de somme des carrés

E = \frac{1}{2}\sum_{k}(y_k - t_k)^2 

y _{k </ sub>: sortie du réseau neuronal t k </ sub>: données enseignant k: nombre de dimensions}

Pour les données de l'enseignant, l'étiquette de réponse correcte est 1 et les autres sont 0. Cette méthode est appelée notation one-hot.

import numpy as np
def mean_squared_error(y,t):
    return 0.5*np.sum((y-t)**2)

Erreur d'entropie croisée

E =- \sum_{k}t_k\log y_k 

import numpy as np
def cross_entropy_error(y,t):
    delta = 1e-7
    return -np.sum(t*np.log(y + delta))

En ajoutant une unité minute, np.log (0) = -inf empêchera le calcul de devenir impossible.

Mini apprentissage par lots

Le problème de l'apprentissage automatique est le travail d'apprentissage utilisant des données d'entraînement → trouver la fonction de perte des données d'entraînement et définir la valeur la plus petite possible.

E = - \frac{1}{N}\sum_{n}\sum_{k}{}t_{nk}\log y_{nk}

Il est normalisé en développant les données N et en divisant finalement par N. L'apprentissage par mini-lots est une méthode dans laquelle seul un certain nombre de feuilles est sélectionné parmi des dizaines de milliers de données d'entraînement et l'apprentissage est effectué pour chaque mini-lot.

Pente

Collecte des différentiels partiels des deux (x _{0 </ sub>, x 1 </ sub>),}

(\frac{\partial f}{\partial x_0},\frac{\partial f}{\partial x_1})

Le gradient est la somme des différentiels partiels de toutes les variables en tant que vecteur.

import numpy as np
def numerical_gradient(f, x):
    h = 1e-4
    grad = np.zeros_like(x)

    for idx in range(x.size):
        tmp_val = x[idx]
        #f(x+h)Calculs de
        x[idx] = tmp_val + h
        fxh1 = f(x)

        # f(x+h)Calculs de
        x[idx] = tmp_val + h
        fxh2 = f(x)

        grad[idx] = (fxh1 - fxh2)/(2*h)
        x[idx] = tmp_val #Restaurer la valeur

    return grad

La pente pointe dans le sens de la descente à chaque point.

Méthode de gradient

La méthode du gradient consiste à faire bon usage du gradient et à trouver la valeur minimale de la fonction. Dans la méthode du gradient, le véhicule se déplace dans la direction du gradient à partir de l'emplacement actuel sur une certaine distance, trouve le gradient à la destination, puis se déplace dans la direction du gradient à plusieurs reprises. Réduisez progressivement la valeur de la fonction en répétant la direction du dégradé.

x_0 = x_0 - \eta\frac{\partial f}{\partial x_0} \\
x_1 = x_1 - \eta\frac{\partial f}{\partial x_1}

η représente la quantité de mises à jour et est appelé ** taux d'apprentissage ** dans la formation des réseaux neuronaux. C'est une variable qui détermine la quantité à apprendre dans un apprentissage et le nombre de paramètres mis à jour. La formule ci-dessus montre une formule de mise à jour unique, et ceci est répété plusieurs fois. La valeur du taux d'apprentissage doit être déterminée à l'avance, par exemple 0,01 ou 0,001. Il est courant de vérifier si l'apprentissage est correct tout en modifiant la valeur du taux d'apprentissage.

import numpy as np
def numerical_gradient(f, x):
    h = 1e-4
    grad = np.zeros_like(x)

    for idx in range(x.size):
        tmp_val = x[idx]
        #f(x+h)Calculs de
        x[idx] = tmp_val + h
        fxh1 = f(x)

        # f(x+h)Calculs de
        x[idx] = tmp_val + h
        fxh2 = f(x)

        grad[idx] = (fxh1 - fxh2)/(2*h)
        x[idx] = tmp_val #Restaurer la valeur

    return grad

def gradient_descent(f,init_x,lr=0.01,step_num=100):
    x = inti_x

    for i in range(step_num):
        grad = numerical_gradient(f,x)
        x -= lr * grad

    return x

J'utilise la fonction pour trouver le dégradé. lr représente le taux d'apprentissage et step_num représente le nombre d'itérations par la méthode du gradient.

Gradient par rapport au réseau neuronal

Le gradient dans le réseau neuronal est le gradient de la fonction de perte par rapport au paramètre de poids. Si le poids est W et la fonction de perte est L, le gradient est

\frac{\partial L}{\partial W}

Ce sera.

Algorithme d'apprentissage

import sys, os
sys.path.append(os.pardir)
from common.functions import *
from common.gradient import numerical_gradient

class TwoLayerNet:
    
    #Initialiser l'entrée_size est le nombre de neurones dans la couche d'entrée, masqués_size est le nombre de neurones dans la couche cachée, sortie_la taille est le nombre de neurones dans la couche de sortie
    def __init__(self, input_size, hidden_size, output_size, weight_init_std=0.01):
        #Initialisation du poids
        self.params = {}
        self.params['W1'] = weight_init_std * np.random.randn(input_size, hidden_size)#Aléatoire
        self.params['b1'] = np.zeros(hidden_size)
        self.params['W2'] = weight_init_std * np.random.randn(hidden_size, output_size)#Aléatoire
        self.params['b2'] = np.zeros(output_size)
        
    def predict(self, x):
        W1, W2 = self.params['W1'], self.params['W2'] #Paramètres de poids de substitution
        b1, b2 = self.params['b1'], self.params['b2']#Remplacer les paramètres de biais
        
        a1 = np.dot(x, W1) + b1#Poids de la première couche x calcul du signal d'entrée + biais
        z1 = sigmoid(a1) #Convertir a1 calculé ci-dessus avec la fonction sigmoïde
        a2 = np.dot(z1, W2) + b2 #Poids de la deuxième couche*Calcul de z1+biais
        y = softmax(a2) #Passez a2 calculé ci-dessus à y, qui est la couche de sortie
        
        return y

    # x:Données d'entrée, t:Données des enseignants
    def loss(self, x, t):#Fonction de perte
        y = self.predict(x)#Instance de classe TwoLayerNet, prédire(x)Renvoie le résultat de.
        
        return cross_entropy_error(y, t)#Le résultat est appliqué à l'erreur d'entropie croisée et l'erreur est calculée en comparant avec les données de l'enseignant. À
    
    #Calculez le taux de réponse correct. Précision de reconnaissance
    def accuracy(self, x, t):
        y = predict(x) #predict(x)Je calcule, mais je me demande si je n'ai pas besoin de moi?
        y = np.argmax(y, axis=1)#Avec argmax, seules les étiquettes avec des nombres élevés sont supprimées.
        t = np.argmax(t, axis=1)#Utilisez argmax pour récupérer l'étiquette correcte.
        
        accuracy = np.sum(y == t)/float(x.shape[0])#y==Si t est Vrai, additionnez-les à 1 et divisez-le par le nombre total de données.
        return accuracy
    
    # x:Des données d'entrée, t:Données des enseignants
    #Trouvez la différenciation partielle et le gradient
    def numerical_gradient(self, x, t):
        loss_W = lambda W: self.loss(x, t) #fonction anonyme lambda, lambda x:y x est l'argument et y est la valeur de retour
        # def loss_W(W):
        #   self.loss(x,t)Devrait avoir la même signification que.
        
        grads = {}#Initialisez les diplômés.
        grads['W1'] = numerical_gradient(loss_W, self.params['W1'])#Gradient de poids de la première couche. Calculé à partir de la fonction de perte et du poids.
        grads['b1'] = numerical_gradient(loss_W, self.params['b1'])#Le gradient du biais de la première couche. Calculé à partir de la fonction de perte et du poids.
        grads['W2'] = numerical_gradient(loss_W, self.params['W2'])#Le gradient du poids de la deuxième couche. Calculé à partir de la fonction de perte et du poids.
        grads['b2'] = numerical_gradient(loss_W, self.params['b2'])#Le gradient du biais de la deuxième couche. Calculé à partir de la fonction de perte et du poids.
        
        return grads