J'ai essayé de vérifier la meilleure façon de trouver un bon partenaire de mariage
Selon le taux actuel de célibataires à vie au Japon, un homme sur quatre et une femme sur sept n'ont jamais été mariés avant l'âge de cinquante ans, et la proportion de ces personnes continuera d'augmenter. (Source: Huffington Post). Il semble y avoir plusieurs causes, mais il semble que la raison ** "Je ne peux pas rencontrer la bonne personne" ** arrive en tête.
Mais quel genre de personne est la bonne personne?
Il y a diverses conditions que les gens veulent les uns des autres, comme le revenu annuel, l'apparence, la personnalité, la maison, etc., mais même si vous pouvez rencontrer un bon partenaire, vous pouvez dire: «Peut-être une meilleure personne dans le futur». Vous pouvez souvent rater une opportunité en vous demandant si vous pouvez vous rencontrer ... "(larmes)
Le problème est que si M. A cherche un conjoint,
- M. A rencontre N personnes et femmes candidates au mariage
- Les candidats adversaires apparaissent les uns après les autres
- Les candidats adversaires ont des scores différents
- M. A veut épouser une personne avec le score le plus élevé possible
- Les candidats peuvent se marier si M. A dit Oui. Mais je ne peux plus rencontrer le reste des candidats
- Les candidats partiront lorsque M. A dit non et ne pourront plus se réunir
Il peut être simplifié en un jeu avec la règle. Ce problème est appelé le ** problème du secrétaire ** et il existe une stratégie mathématiquement optimale. C'est,
- Les premiers 37% disent non, quel que soit le score
- Pour les personnes après cela, si le score de cette personne est le plus élevé jamais enregistré, choisissez cette personne
C'est vraiment simple. À proprement parler, 37% correspond à ** 1 / e **. Cette stratégie semble augmenter les chances d'épouser un adversaire au score élevé quel que soit le nombre d'adversaires candidats N.
Même quand j'entends ça, je pense honnêtement "Est-ce vraiment?" Je comprends que je dois fixer un seuil quelque part, mais je sens que je peux trouver un meilleur partenaire, comme 50% ou 80% après avoir attendu plus longtemps, au lieu de la valeur impaire de 37%.
Cette fois, j'aimerais utiliser une simple simulation pour tester cette stratégie.
Mise en œuvre de la stratégie
Je vais calculer en utilisant Python3. Tout d'abord, mettez les bibliothèques requises.
# import libraries
import random
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
La fonction principale prend en entrée le nombre de candidats et le nombre de personnes qui se rencontrent avant de créer un seuil, et sélectionne la personne qui dépasse le seuil pour la première fois. Le rang et le score de l'adversaire sont affichés. Supposons que le score du candidat prenne une valeur entière aléatoire de 0 à 100.
# function to find a partner based on a given decision-time
def getmeplease(rest, dt, fig):
## INPUT: rest ... integer representing the number of the fixed future encounters
# dt ... integer representing the decision time to set the threshold
# fig ... 1 if you want to plot the data
# ++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
# score ranging from 0 to 100
scoremax = 100
#random.seed(1220)
# sequence of scores
distribution = random.sample(range(scoremax), k=rest)
# visualize distribution
if fig==1:
# visualize distribution of score
plt.close('all')
plt.bar(range(1,rest+1), distribution, width=1)
plt.xlabel('sequence')
plt.ylabel('score')
plt.xlim((0.5,rest+0.5))
plt.ylim((0,scoremax))
plt.xticks(range(1, rest+1))
# remember the highest score among the 100 x dt %
if dt > 0:
threshold = max(distribution[:dt])
else:
threshold = 0
# pick up the first one whose score exceeds the threshold
partner_id = 1
partner_score = distribution[0]
t = dt
for t in range(dt+1, rest):
if partner_score < threshold:
partner_score = distribution[t]
else:
partner_id = t
break
else:
partner_score = distribution[-1]
partner_id = rest
# get the actual ranking of the partner
array = np.array(distribution)
temp = array.argsort()
ranks = np.empty(len(array), int)
ranks[temp] = np.arange(len(array))
partner_rank = rest - ranks[partner_id-1]
# visualize all
if fig==1:
plt.plot([decisiontime+0.5,decisiontime+0.5],[0,scoremax],'--k')
plt.bar(partner_id,partner_score, color='g', width=1)
return [partner_id, partner_score, partner_rank]
Par exemple, si le nombre de candidats est de 10 et le nombre de personnes que vous rencontrez avant de définir un seuil est de 4 personnes, soit environ 37% de cela, cette fonction getmeplease (10,4,1) dessine le graphique suivant.

…… J'ai pu épouser la personne avec le score le plus élevé qui est apparue 8e sur 10 personnes ((((o ノ ´3 `) ノ génial (yeux blancs)
simulation
Préparez 4 modèles de 5, 10, 20, 100 pour le nombre de personnes N à rencontrer. De même, j'aimerais préparer et comparer quatre schémas de stratégies lorsque le nombre de personnes rencontrées avant de créer un seuil est porté à 10%, 37%, 50%, 80% du total.
Dans la fonction suivante, chaque stratégie («optimale»: 37%, «précoce»: 10%, «tard»: 80%, «moitié»: 50%) est simulée 10000 fois avec le rang de l'adversaire sélectionné. Faites un histogramme des scores et trouvez la médiane.
# parameters
repeat = 10000
rest = [5,10,20,100]
opt_dt = [int(round(x/np.exp(1))) for x in rest]
tooearly_dt = [int(round(x*0.1)) for x in rest]
toolate_dt = [int(round(x*0.8)) for x in rest]
half_dt = [int(round(x*0.5)) for x in rest]
# initialization
opt_rank = np.zeros(repeat*len(rest))
early_rank = np.zeros(repeat*len(rest))
late_rank = np.zeros(repeat*len(rest))
half_rank = np.zeros(repeat*len(rest))
opt_score = np.zeros(repeat*len(rest))
early_score = np.zeros(repeat*len(rest))
late_score = np.zeros(repeat*len(rest))
half_score = np.zeros(repeat*len(rest))
# loop to find the actual rank and score of a partner
k = 0
for r in range(len(rest)):
for i in range(repeat):
# optimal model
partner_opt = getmeplease(rest[r], opt_dt[r], 0)
opt_score[k] = partner_opt[1]
opt_rank[k] = partner_opt[2]
# too-early model
partner_early = getmeplease(rest[r], tooearly_dt[r], 0)
early_score[k] = partner_early[1]
early_rank[k] = partner_early[2]
# too-late model
partner_late = getmeplease(rest[r], toolate_dt[r], 0)
late_score[k] = partner_late[1]
late_rank[k] = partner_late[2]
# half-time model
partner_half = getmeplease(rest[r], half_dt[r], 0)
half_score[k] = partner_half[1]
half_rank[k] = partner_half[2]
k += 1
# visualize distributions of ranks of chosen partners
plt.close('all')
begin = 0
for i in range(len(rest)):
plt.figure(i+1)
plt.subplot(2,2,1)
plt.hist(opt_rank[begin:begin+repeat],color='blue')
med = np.median(opt_rank[begin:begin+repeat])
plt.plot([med, med],[0, repeat*0.8],'-r')
plt.title('optimal: %i' %int(med))
plt.subplot(2,2,2)
plt.hist(early_rank[begin:begin+repeat],color='blue')
med = np.median(early_rank[begin:begin+repeat])
plt.plot([med, med],[0, repeat*0.8],'-r')
plt.title('early: %i' %int(med))
plt.subplot(2,2,3)
plt.hist(late_rank[begin:begin+repeat],color='blue')
med = np.median(late_rank[begin:begin+repeat])
plt.plot([med, med],[0, repeat*0.8],'-r')
plt.title('late: %i' %int(med))
plt.subplot(2,2,4)
plt.hist(half_rank[begin:begin+repeat],color='blue')
med = np.median(half_rank[begin:begin+repeat])
plt.plot([med, med],[0, repeat*0.8],'-r')
plt.title('half: %i' %int(med))
fig = plt.gcf()
fig.canvas.set_window_title('rest' + ' ' + str(rest[i]))
begin += repeat
plt.savefig(figpath + 'rank_' + str(rest[i]))
begin = 0
for i in range(len(rest)):
plt.figure(i+10)
plt.subplot(2,2,1)
plt.hist(opt_score[begin:begin+repeat],color='green')
med = np.median(opt_score[begin:begin+repeat])
plt.plot([med, med],[0, repeat*0.8],'-r')
plt.title('optimal: %i' %int(med))
plt.subplot(2,2,2)
plt.hist(early_score[begin:begin+repeat],color='green')
med = np.median(early_score[begin:begin+repeat])
plt.plot([med, med],[0, repeat*0.8],'-r')
plt.title('early: %i' %int(med))
plt.subplot(2,2,3)
plt.hist(late_score[begin:begin+repeat],color='green')
med = np.median(late_score[begin:begin+repeat])
plt.plot([med, med],[0, repeat*0.8],'-r')
plt.title('late: %i' %int(med))
plt.subplot(2,2,4)
plt.hist(half_score[begin:begin+repeat],color='green')
med = np.median(half_score[begin:begin+repeat])
plt.plot([med, med],[0, repeat*0.8],'-r')
plt.title('half: %i' %int(med))
fig = plt.gcf()
fig.canvas.set_window_title('rest' + ' ' + str(rest[i]))
begin += repeat
plt.savefig(figpath + 'score_' + str(rest[i]))
Lorsque N = 20
Lors de la rencontre de 20 personnes, la répartition des scores et des classements est la suivante.
Rang
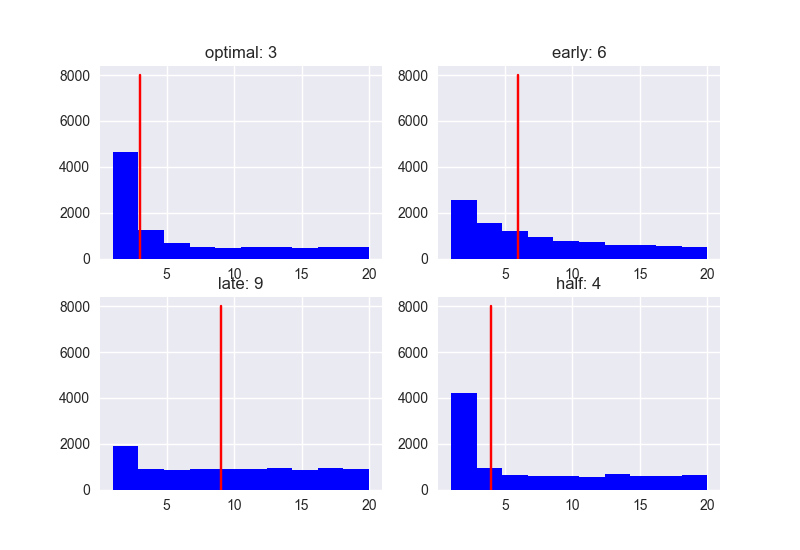
Avec la stratégie optimale (37%), le rang médian était de 3. Si vous approchez avec la stratégie «Non pour les premiers 37%, puis Oui pour la personne avec le score le plus élevé», vous pourrez épouser la personne dans le tiers des personnes que vous pouvez rencontrer avec une forte probabilité. ..
À propos, les valeurs médianes pour Early (10%) et Half (50%) sont respectivement de 6 et 4, donc ce n'est pas mal du tout (?). Le retard (80%) a une médiane de 9, donc les chances d'échec sont élevées. .. ..
Et le score?

Avec la stratégie Optimal (37%), le score médian était de 89. D'autres stratégies ont 78 pour Early (10%), 59 pour Late (80%) et 86 pour Half (80%), les performances sont donc toujours élevées lorsque le seuil est défini sur ** 1 / e **. n'est-ce pas. Il semble qu'il sera plus facile de choisir une meilleure personne. La meilleure stratégie ne mène pas toujours à la meilleure solution, mais elle peut augmenter la probabilité d'approcher la meilleure solution.
En prime, je listerai également le nombre de candidats pour 5, 10 et 100.
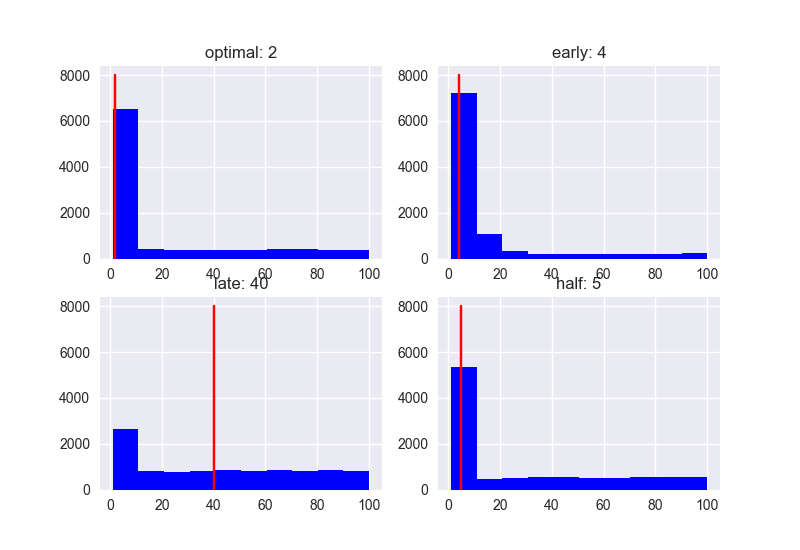
N = 5 ###
Rang

But
N = 10 ###
Rang

But

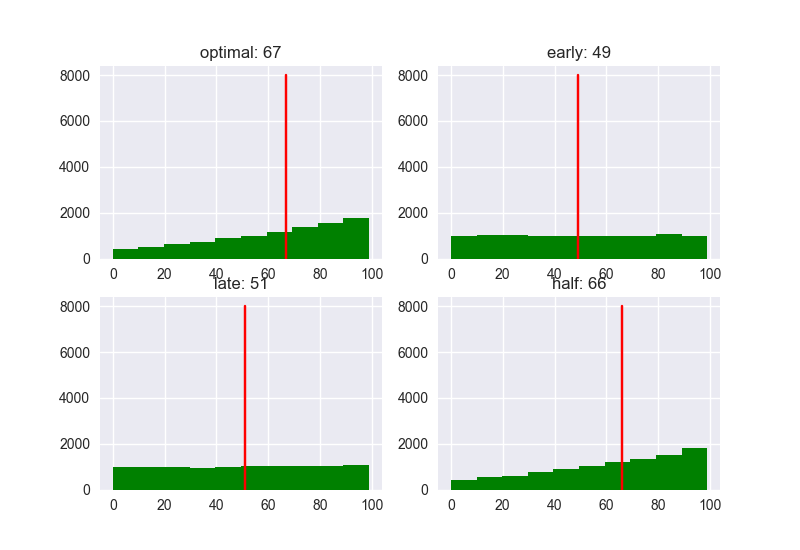
N = 100 ###
Rang
But

La tendance évidente est que la performance des «retard» se détériore à mesure que le nombre de candidats augmente. Si le nombre de candidats est petit, la différence de performance en fonction de la stratégie est faible, mais la valeur du score a tendance à être faible. Dans tous les cas, il semble probable que la stratégie consistant à rencontrer d'abord 37% des personnes pour fixer le seuil sera celle avec le rang le plus élevé et le score le plus élevé.
Conclusion
«Plus vous avez de candidats, plus vous avez de chances de rencontrer de meilleurs adversaires. «Cependant, si vous vous trompez avec" Pensez plus ... ", non seulement vous perdrez des opportunités, mais le score de la personne finale va également empirer. ――Mais peu importe s'il est trop tôt ――Il semble que la meilleure stratégie soit de décider du nombre de personnes que vous rencontrerez à l'avenir, de rencontrer les personnes 1 / e pour fixer le seuil, puis de décider de la personne qui dépasse le seuil pour la première fois.
Mise en garde
`` En réalité, même si vous dites oui, l'autre partie dit souvent non. ―― ~~ Les gens qui écrivent du code à la maison pendant les vacances ~~ n'ont souvent aucun candidat en premier lieu
- ** Adopter la stratégie optimale ne signifie pas que vous obtiendrez la solution optimale **
……Faisons de notre mieux!
Référence
Article du Huffington Post Conférence TED * Hannah Fly-Mathematics to Talk about Love- [Article du Washington Post](https://www.washingtonpost.com/news/wonk/wp/2016/02/16/when-to-stop-dating-and-settle-down-according-to-math/ ? utm_term = .ee305554c210)