Prédire les données de séries chronologiques avec un réseau neuronal
Lorsque vous traitez des données de séries chronologiques dans un réseau neuronal, utilisez un réseau neuronal récurrent. Cette fois, je vais vous expliquer le réseau de neurones récurrent.
(Parce qu'il est long, le réseau neuronal est abrégé en NN, et le réseau neuronal récurrent est abrégé en RNN)
Présentation de RNN
Dans certaines données, les données précédentes ont une corrélation avec les données suivantes, par exemple lorsqu'un "x" apparaît, il y a une forte possibilité qu'un "y" vienne. Plus précisément, c'est quelque chose comme des mots ou de la musique (comme «ha» ou «ga» vient souvent après «je»). Pour de telles données corrélées de séries chronologiques, il est naturellement tentant de considérer des données précédemment générées. Est-il possible de saisir des données précédemment générées dans NN? La réponse est RNN.
Plus précisément, c'est comme le montre la figure ci-dessous.

Le contenu de la couche cachée au temps $ t $ sera traité comme entrée à la prochaine fois $ t + 1 $. La couche cachée de $ t + 1 $ continue avec $ t + 2 $ ..., mais le fait est que la couche cachée précédente est également utilisée pour apprendre la couche cachée suivante.
Type RNN
| Nom | Cible combinée | Fonctionnalité |
|---|---|---|
| Fully recurrent network | Tous les nœuds(1:N) | Combinez complètement bidirectionnellement, y compris lui-même |
| Hopfield network | Tous les nœuds(1:N-1) | Jointure bidirectionnelle, ne s'inclut pas dans la cible de jointure |
| Elman network | 1:1 (Couche cachée->Couche cachée) | Couche d'entrée / contexte(Couche cachée)・ Structure à trois couches de la couche de sortie |
| Jordan network | 1:1 (Couche de sortie->Couche cachée) | Couche d'entrée / contexte(Couche cachée)・Couche de sortieの3層構造 |
| Echo state network (ESN) | 1->1? | La cible de la jointure est un ensemble de nœuds(reservoir)Déterminé aléatoirement à partir de |
| Long short term memory network (LSTM) | - | Au lieu du nœud RNN, un bloc qui peut contenir la valeur d'entrée est adopté. Haute précision |
| Bi-directional RNN (BRNN) | - | Bidirectionnel(passé->futur/futur->passé)Une combinaison de RNN |
Réseau Hopfield a applicable aux problèmes d'optimisation en plus de la classification générale. /~kanakubo/research/neuro/hopfieldnetwork.html) Ceci est un modèle.
Elman / Jordan est la forme la plus simple comme on l'appelle Réseaux récurrents simples. Si vous souhaitez utiliser RNN, essayez d'abord l'un ou l'autre, et s'il y a un problème de précision, essayez de passer à une autre méthode. La différence entre Elman / Jordan est comme ci-dessus (que les données précédentes soient reflétées depuis la couche cachée ou la couche de sortie), mais ici Il est également écrit en détail dans. Il n'y a pas d'avantage exact, mais je pense qu'Elman est plus flexible car la quantité de propagation suivante peut être modifiée en fonction du nombre de couches cachées.
Echo state network est un modèle avec une couleur de cheveux différente, et les nœuds ne sont pas combinés à l'avance et stockés dans un pool appelé Reservoir (ce qui signifie réservoir, etc.). C'est un style qui se joint de manière aléatoire / dynamique après que l'entrée est donnée. Le fait est qu'il n'y a pas de connexion prédéterminée dans le cerveau humain, il a donc été créé avec le concept de l'imiter et de se connecter de manière fluide. Il semble que cela s'appelle aussi Liquid State Machines (littéralement, mécanisme liquide).
Le réseau de mémoire à long terme (LSTM) et le RNN bidirectionnel (BRNN) n'ont aucune restriction particulière sur la façon de se joindre. LSTM adopte un bloc LSTM qui peut mémoriser des poids au lieu de simples nœuds. Ceci est pour résoudre les défis d'apprentissage dans RNN et sera expliqué plus tard.
Le RNN bidirectionnel peut améliorer la précision non seulement en apprenant dans une direction du passé vers le futur, mais également en apprenant les séries chronologiques dans une certaine direction négative du futur au passé.
Apprendre RNN
Les documents suivants sont très soigneusement rédigés sur l'apprentissage de RNN. Bien qu'il soit en anglais, il n'y a presque pas de littérature japonaise sur RNN à ce stade (2015/1), il n'y a donc pas d'autre choix que d'abandonner et de le lire.
L'apprentissage RNN est généralement très lent à converger. Vous devez réduire le taux d'apprentissage pour la précision, mais l'abaisser ralentira la convergence déjà lente. C'est un compromis, mais il semble y avoir un moyen de le résoudre en tenant compte de l'instabilité du gradient dans le processus d'optimisation (voir [ALGORITHMES D'APPRENTISSAGE DE SECOND ORDRE EFFICACES POUR RÉSEAUX NEURAUX RÉCURRENTS À TEMPS DISCRET] pour plus de détails]. (Voir http://ir.nmu.org.ua/bitstream/handle/123456789/120274/866d31771b48ba40c56fcc039f091b9b.pdf?sequence=1&isAllowed=y#page=58).
Une chose que je peux dire est que, pour le moment (2015/1), il n'y a pas de méthode établie qui ne pose aucun problème de précision et de vitesse dans l'apprentissage RNN, donc bien sûr il n'y a pas de bibliothèque qui l'implémente. .. Il est nécessaire de pratiquer régulièrement ici.
BPTT (BackPropagation Through Time) L'idée de base est que la rétropropagation doit être applicable comme d'habitude, car les RNN peuvent être considérés comme des NN longs lorsqu'ils sont développés. L'image est la suivante.

L'erreur se propage du dernier temps T au premier 0. Par conséquent, l'erreur de la couche de sortie à un certain instant t est la somme de «la différence entre l'enseignant (données de l'enseignant) et la sortie (sortie) au temps t» et «l'erreur propagée à partir de t + 1».
Comme le montre clairement la figure, BPTT ne peut pas s'entraîner sans les données jusqu'au dernier T, c'est-à-dire toutes les données de la série chronologique. Par conséquent, il est nécessaire de prendre des mesures telles que supprimer uniquement les dernières données pour les données longues.
Ce BPTT présente divers problèmes et diverses méthodes d'apprentissage ont été conçues pour y faire face.
LSTM(Long short term memory) Si T est trop grand, c'est-à-dire pour des données de séries chronologiques longues, l'erreur de la couche supérieure peut être diminuée ou inversement très importante en raison d'un problème de calcul (ceci est détaillé ici (p8 ~)]( http://www.slideshare.net/beam2d/pfi-seminar-20141030rnn)). À mesure que la valeur augmente, la valeur maximale est limitée, mais elle ne peut pas être empêchée de disparaître, donc l'idée du LSTM est de propager l'erreur afin qu'elle ne se décompose pas.
teacher forcing Dans RNN, la sortie de t devient l'entrée de t + 1 et ainsi de suite, mais au moment de l'apprentissage, la réponse correcte de l'entrée à t + 1 est claire de la part de l'enseignant, donc la méthode pour l'utiliser telle quelle est. Cela permet d'entraîner chaque couche en ignorant l'influence de la couche inférieure et d'augmenter la vitesse de convergence, mais il semble que la sortie n'est pas stable lorsqu'elle est réellement exécutée (après apprentissage).
RPROP(Resilient backpropagation) C'est la méthode également utilisée pour les NN réguliers. Lors de l'apprentissage de NN, le gradient est calculé, mais il est pondéré ($ \ eta $) en fonction de la façon dont la direction (signe) du gradient a changé entre la dernière fois et maintenant (voir [ici](http pour plus de détails). Vous pouvez en savoir plus sur //paginas.fe.up.pt/~ee02162/dissertacao/RPROP%20paper.pdf).
- Si le signe est le même entre l'instant précédent et cette fois, l'apprentissage est accéléré en pondérant le gradient.
- Si le signe est différent entre l'instant précédent et cette fois, le gradient est décéléré et la solution revient à la solution optimale négligée.
Je pense que cela s'appelle Résilient parce que ce comportement ressemble à faire rouler une balle (accélération sur un gradient, ralentissement lorsque le gradient change de direction et exerçant une force dans la direction opposée). ..
Avec une fonction comme la fonction Sigmoïde, l'apprentissage sera difficile à réaliser car il sera plat (le gradient est presque 0) où la valeur dépasse une certaine plage (Flat Spot Problem. wiki / Flat_Spot_Problem))), l'application de cette méthode a également pour effet d'éviter la stagnation d'apprentissage due au poids.
Il existe de nombreuses variantes de cette technique elle-même. Pour plus de détails, veuillez consulter ici.
En plus des diverses méthodes décrites ci-dessus, il est également important d'ajuster des paramètres tels que le taux d'apprentissage qui ajuste le degré de propagation d'erreur et l'élan qui ajuste l'influence de la couche précédente, comme avec NN normal.
Le BPTT est généralement lent à converger et prend beaucoup de temps à apprendre. Par conséquent, les nœuds de couche cachée sont souvent utilisés dans de petits réseaux d'environ 3 à 20, et s'ils le dépassent, l'apprentissage peut prendre plusieurs heures, voire plus.
RTRL (Real Time Recurrent Learning) Contrairement à BPTT, RTRL est une méthode de propagation des erreurs dans le futur, ce qui le rend approprié pour l'apprentissage en ligne.

Met à jour le poids à l'instant t + 1 suivant avec l'erreur survenue au temps t. Dans la figure ci-dessus, l'erreur est calculée et propagée à chaque instant, mais il existe également une méthode de mise à jour après un certain laps de temps (époque). Cependant, comme le poids qui doit être mis à jour en une seule fois est supérieur à celui du BPTT, la charge de calcul est élevée.
EKF (Extended Kalman Filter) C'est EKF qui applique le filtre de Kalman étendu à RNN et met à jour le poids. Le filtre de Kalman étendu est une extension non linéaire du filtre de Kalman qui gère les systèmes linéaires et estime l'état du système comme suit.
$ x(n+1) = f(x(n)) + q(n) $ $ d(n) = h_n(x(n)) $
La formule ci-dessus exprime ce qui suit.
- L'état suivant $ x (n + 1) $ représente l'entrée $ f (x (n)) $ de l'état précédent $ x (n) $ et $ q (n) $ (bruit externe) Est déterminé par
- La sortie de l'état $ x (n) $ est $ h_n (x (n)) $
L'image est comme indiqué dans la figure ci-dessous.

Et RNN peut être considéré comme ce filtre de Kalman étendu. La figure ci-dessous le montre.
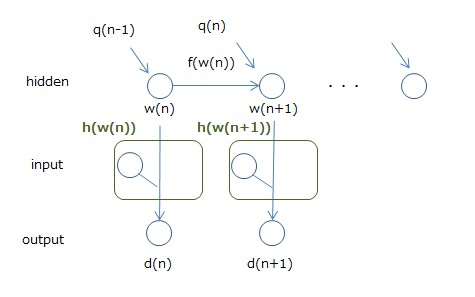
Je pense que c'est correct d'avoir le poids $ w $ comme état et la sortie comme $ d $. Le problème est l'entrée, mais en la considérant comme faisant partie de la fonction $ h $ pour calculer la sortie $ d $, nous disons que c'est un filtre de Kalman étendu (en fait l'entrée et les poids de l'entrée). Il est calculé en $ w $, donc je ne pense pas que ce soit trop difficile).
Ensuite, le procédé de mise à jour de l'état du filtre de Kalman étendu peut être appliqué tel quel à la mise à jour de l'état de RNN, c'est-à-dire le poids. La formule de mise à jour de l'état est assez compliquée, je vais donc omettre les détails, mais la méthode appelée EKF apporte la méthode du filtre de Kalman étendu à RNN de cette manière. Il existe également une méthode pour simplifier le calcul, qui est une méthode prometteuse, mais comme BPTT et RTRL, un réglage empirique (taux d'apprentissage, configuration du réseau, etc.) est nécessaire pour atteindre la précision.
Bibliothèque RNN
Pybrain est clairement pris en charge par les principales bibliothèques. Un didacticiel de réseau récurrent (http://pybrain.org/docs/tutorial/netmodcon.html#using-recurrent-networks) est également disponible.
Il semble que cela soit possible avec pylearn2, qui est célèbre pour le Deep Learning, mais comme vous pouvez le voir sur le chemin, il est toujours dans le bac à sable pour le moment (2015/1), et il est dans un état difficile de l'utiliser.
lisa-lab/pylearn2 pylearn2/pylearn2/sandbox/rnn/models/tests/test_rnn.py
Si vous souhaitez l'implémenter vous-même, la méthode utilisant Theano est introduite.
Implementing a recurrent neural network in python gwtaylor/theano-rnn
Il s'agit d'une combinaison de RNN et RBM, mais l'implémentation comprenant le code est introduite.
Modeling and generating sequences of polyphonic music with the RNN-RBM Introduction à la prédiction et à la génération de mélodie par RNN-RBM et au traitement de l'information musicale
De plus, neuraltalk semble être un modèle qui entraîne une image et son explication, et en fournit une explication lorsqu'une image est donnée. C'est une bibliothèque prête à l'emploi plutôt qu'une bibliothèque pour la construction, mais je pense que c'est bien de l'utiliser à cette fin.
Implémentation RNN
Cette fois, je vais implémenter RNN en utilisant «pybrain», qui a un exemple d'implémentation comme décrit ci-dessus.
La dernière version de PyBrain est la 0.3.3 (à partir de janvier 2015). Il semble qu'il ait été téléchargé sur le site PYPI (https://pypi.python.org/pypi/PyBrain/0.3.3) ... mais comme il est 0.3.2 d'entrer depuis pip, `git clone Déposez le référentiel avec ʻet installez-le. Veuillez vous référer ici pour la procédure et les bibliothèques dépendantes.
La dépendance principale est Scipy. Python est écrit en 2.5, mais j'ai confirmé que le test (python runtests.py) peut être passé avec Python 3.4.2 dans mon environnement. En regardant les problèmes, etc., il semble que Python 3 a des parties non prises en charge, mais il n'y a eu aucun problème lors de son utilisation (à moins qu'il y ait eu une erreur sans le savoir ...).
Pour les données de séries temporelles prévues, nous avons généré et utilisé des données de trajectoire de balle. Données liées à la balle (www.cs.utoronto.ca/~ilya/code) initialement utilisées dans cet article J'ai essayé d'utiliser /2008/RTRBM.tar), mais l'environnement d'exploitation est ancien comme Python2, et si vous en croyez la description dans README, il faudra une semaine pour apprendre (citation: les problèmes de balles rebondissantes s'entraînent pour une quantité considérablement plus longue) Puisqu'il était temps (environ une semaine sur un ordinateur rapide ...)), j'ai décidé de générer et d'utiliser une trajectoire simple.
La construction du modèle est soigneusement décrite dans le didacticiel PyBrain, mais les principales méthodes de description sont résumées ci-dessous.
Welcome to PyBrain’s documentation!
Construire un réseau
Assemblez en utilisant pybrain.structure. Dans ce qui suit, nous construisons un réseau normal avec un terme de biais en 2-3-1.
Building Networks with Modules and Connections
from pybrain.structure import FeedForwardNetwork, LinearLayer, SigmoidLayer, BiasUnit, FullConnection
net = FeedForwardNetwork()
net.addInputModule(LinearLayer(2, name='i'))
net.addModule(BiasUnit('bias'))
net.addModule(SigmoidLayer(3, name='h'))
net.addOutputModule(LinearLayer(1, name='o'))
# connect nodes
net.addConnection(FullConnection(net['i'], net['h']))
net.addConnection(FullConnection(net['bias'], net['h']))
net.addConnection(FullConnection(net['bias'], net['o']))
net.addConnection(FullConnection(net['h'], net['o']))
Il est plus facile de créer avec buildNetwork. Ce qui suit est le même que le processus ci-dessus.
net = buildNetwork(2, 3, 1, bias=True, hiddenclass=SigmoidLayer)
Apprendre le réseau
Pour faire la formation, préparez d'abord un jeu de données. Dans ce qui suit, les données de la sortie 1 sont passées comme ʻaddSample pour l'entrée 2 selon le réseau construit ci-dessus (notez que ʻappendLinked et ʻaddSample` apparaissant dans le document sont équivalents //github.com/pybrain/pybrain/blob/1dd5086a51c3c98497ef85b31178588a89d8951e/pybrain/datasets/unsupervised.py#L31)).
from pybrain.datasets import SupervisedDataSet
ds = SupervisedDataSet(2, 1)
ds.addSample((0, 0), (0,))
...
La formation sera effectuée à l'aide de l'ensemble de données préparé. trainer.train renvoie un double proportionnel à l'erreur, ce qui vous permet d'évaluer l'ajustement à vos données d'entraînement.
Training your Network on your Dataset
from pybrain.supervised.trainers import BackpropTrainer
net = buildNetwork(2, 3, 1, bias=True, hiddenclass=TanhLayer)
trainer = BackpropTrainer(net, ds)
err = trainer.train()
Prédiction de réseau
La prédiction se fait avec la fonction ʻactiver`.
net.activate([1, 2])
Bâtiment RNN
Dans le cas de RNN, c'est presque la même chose qu'une construction de réseau normale.
RNN utilise RecurrentNetwork, et lors d'une connexion récursive, connectez-vous avec ʻaddRecurrentConnection`.
Ensuite, la prédiction est exécutée par ʻactivate après une réinitialisation avec net.reset () . Pour ʻactiver, dans l'exemple ci-dessus, j'ai prédit en saisissant la même valeur tout le temps, mais en réalité, ce n'était pas vrai à moins que je ne saisisse à nouveau la valeur prédite et que je ne le fasse (en théorie, même la première entrée). Si c'est le cas, on peut le prédire de plus en plus par la suite, donc j'ai l'impression qu'il n'y a pas de problème même si la valeur initiale est utilisée ...).
Cette fois, je l'ai essayé avec Elman et Jordan. Ci-dessous, une image en Jordanie. Les coordonnées x et y et leurs accélérations respectives sont transmises comme entrées.

Puisque l'accélération est déterminée par la position du temps t et la position du temps t + 1, je pensais qu'elle apprendrait bien dans la couche cachée ... mais je l'ai ajoutée comme paramètre d'entrée car elle n'était pas précise.
Pour les données d'entraînement, nous avons préparé plusieurs lots avec des positions initiales différentes sous la même accélération initiale, et formé / testé avec eux. Étant donné que l'accélération initiale est la même pour les données d'entraînement / de test, ce modèle est un modèle qui estime le type de trajectoire qui sera dessiné lorsque la balle est placée à un certain point sous cette accélération.
C'est une précision intéressante, mais l'erreur avec les données de test était d'environ 5,7 en moyenne, ce qui n'était pas très bon. Puisque ces données prédit la trajectoire d'une balle rebondissant dans un carré de 10x10, une erreur de 5,7 est un niveau qui peut être considéré comme presque complètement faux.
Bien que cela bouge dans la mesure où vous pouvez comprendre le sentiment dans l'animation, c'est beaucoup pour une reproduction complète. J'ai également essayé d'augmenter ou de réduire les couches et les nœuds cachés, mais cela n'a pas changé.
Orbite réelle
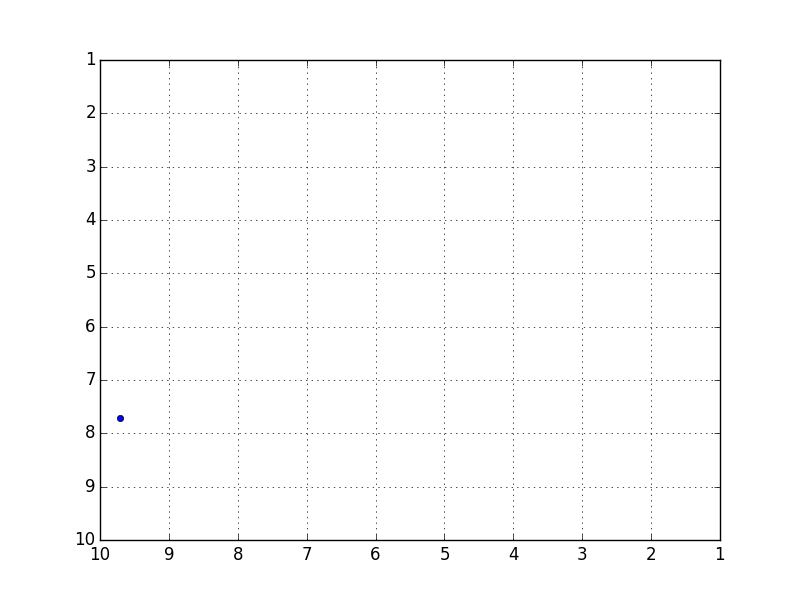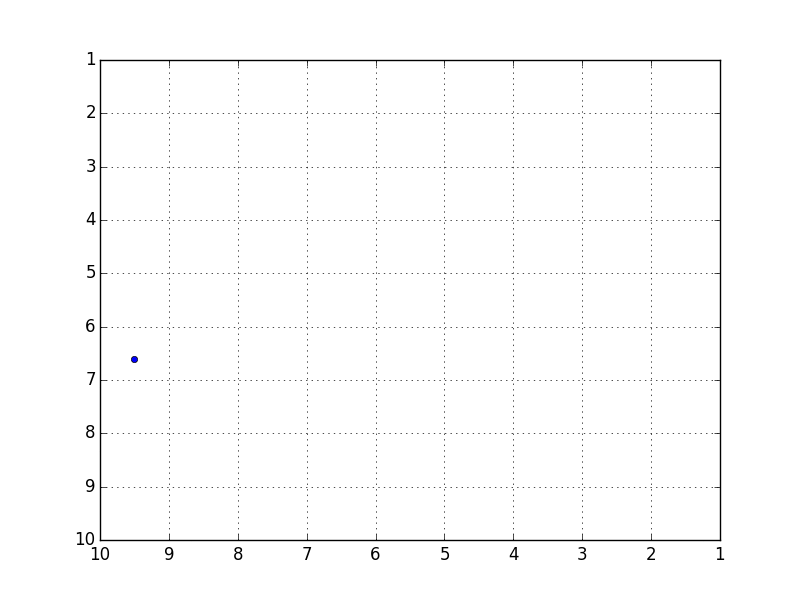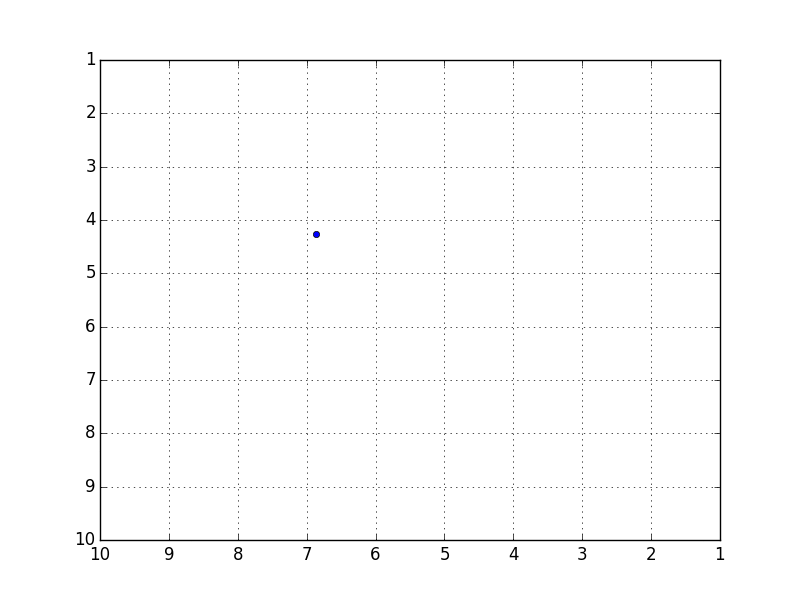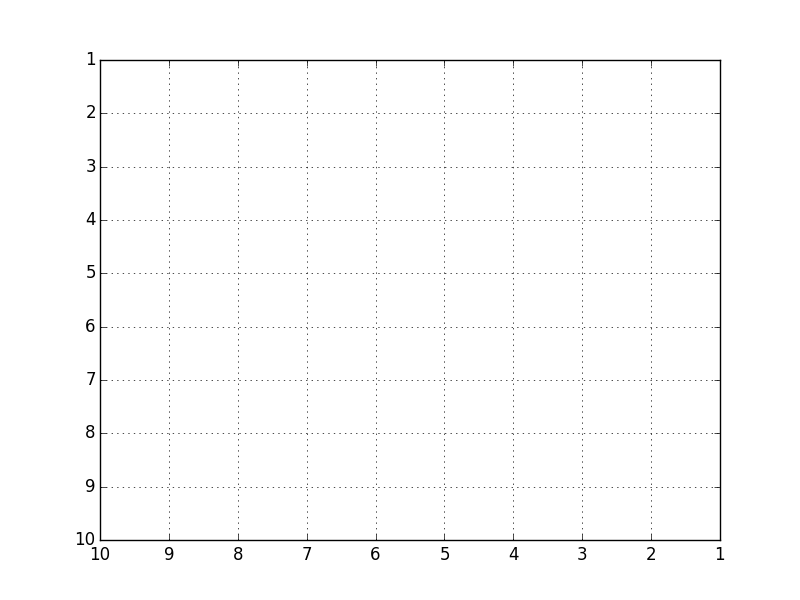
Trajectoire prédite (assez proche du meilleur)

Le code utilisé pour la vérification est ici. Si vous êtes celui qui dit que je suis, j'attends une pull request.
référence
- À propos de RNN
- Recurrent neural network
- Types of artificial neural networks
- Hopfield network
- Echo state network
- What is the difference between Elman and Jordan neural networks
- Recurrent Neural Networks
- Bidirectional recurrent neural networks
- A tutorial on training recurrent neural networks, covering BPPT, RTRL, EKF and the "echo state network" approach
- A Direct Adaptive Method for Faster Backpropagation Learning: The RPROP Algorithm
- Articles sur l'implémentation RNN, etc.
- Modeling and generating sequences of polyphonic music with the RNN-RBM
- Modeling Temporal Dependencies in High-Dimensional Sequences:Application to Polyphonic Music Generation and Transcription
- ↑ Article expliquant l'article en japonais [Introduction à la prédiction et à la génération de mélodie par RNN-RBM et traitement de l'information musicale](http://xiangze.hatenablog.com/entry/2014/09/28/ 143934)
- Continuous time recurrent neural networks for grammatical induction
- À propos de PyBrain
- Welcome to PyBrain’s documentation!
Recommended Posts