3. Traitement du langage naturel par Python 3-1. Important outil d'extraction de mots Analyse TF-IDF [définition originale]
- Lors du traitement du langage naturel, l'un des objectifs spécifiques est "d'extraire des mots importants qui caractérisent une certaine phrase".
- Lors de l'extraction de mots, sélectionnez d'abord les mots qui apparaissent le plus souvent dans le texte. En haut de la liste par ordre de fréquence d'apparition, seuls les mots couramment utilisés dans toutes les phrases.
- Même si vous vous limitez à la nomenclature en utilisant des informations sur une partie de mot, de nombreux mots à usage général qui n'ont pas de signification spécifique, tels que "chose" et "temps", apparaîtront en haut, donc excluez-les comme mots vides. Traitement tel que requis.
⑴ L'idée de TF-IDF
- ** TF-IDF (Fréquence du terme - Fréquence du document inverse) **, littéralement traduit par «Fréquence du terme - Fréquence du document inverse».
- ** L'idée de déterminer qu'un mot qui apparaît fréquemment mais le nombre de documents dans lesquels le mot apparaît est petit **, c'est-à-dire un mot qui n'apparaît pas partout, est un ** mot caractéristique et important ** est.
- La plupart d'entre eux sont pour les mots, mais ils peuvent également être appliqués aux lettres et aux phrases, et les unités des documents peuvent être appliquées de différentes manières.
⑵ Définition de la valeur TF-IDF
** Fréquence d'occurrence $ tf $ multipliée par l'indice de rareté $ idf $ **
tfidf=tf×idf - $ tf_ {ij} $ (fréquence d'occurrence du mot $ i $ dans le document $ j $) × $ idf_ {i} $ ($ log $, l'inverse du nombre de documents contenant le mot $ i $)
** La fréquence d'occurrence $ tf $ et le coefficient $ idf $ sont définis comme suit **
- $ tf_ {ij} = \ dfrac {n_ {ij}} {\ sum_ {k} n_ {kj}} = \ dfrac {nombre d'occurrences du mot i dans le document j} {nombre d'occurrences de tous les mots dans le document j Somme} $
idf_{i}=\log \dfrac{|D|}{|\{d:d∋t_{i}\}|} = \log{\dfrac{Nombre de tous les documents}{Nombre de documents contenant le mot i}}
(3) Mécanisme de calcul basé sur la définition originale
#Import de la bibliothèque de calculs numériques
from math import log
import pandas as pd
import numpy as np
➀ Préparer la liste de données de mots
- Calculez $ tfidf $ des trois mots cibles, en supposant que la liste de mots suivante a été créée pour les six documents après un prétraitement tel qu'une analyse morphologique.
docs = [
["Mot 1", "Mot 3", "Mot 1", "Mot 3", "Mot 1"],
["Mot 1", "Mot 1"],
["Mot 1", "Mot 1", "Mot 1"],
["Mot 1", "Mot 1", "Mot 1", "Mot 1"],
["Mot 1", "Mot 1", "Mot 2", "Mot 2", "Mot 1"],
["Mot 1", "Mot 3", "Mot 1", "Mot 1"]
]
N = len(docs)
words = list(set(w for doc in docs for w in doc))
words.sort()
print("Nombre de documents:", N)
print("Mots cibles:", words)

➁ Définissez une fonction de calcul
- Définissez une fonction qui calcule la fréquence d'occurrence $ tf $, le coefficient $ idf $ et $ tfidf $ multipliés par eux à l'avance.
#Définition de la fonction tf
def tf(t, d):
return d.count(t)/len(d)
#Définition de la fonction idf
def idf(t):
df = 0
for doc in docs:
df += t in doc
return np.log10(N/df)
#Définition de la fonction tfidf
def tfidf(t, d):
return tf(t,d) * idf(t)
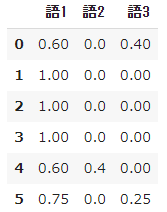
➂ Observez le résultat du calcul de TF
- Pour référence, jetons un œil aux résultats des calculs de $ tf $ et $ idf $ étape par étape.
#Calculer tf
result = []
for i in range(N):
temp = []
d = docs[i]
for j in range(len(words)):
t = words[j]
temp.append(tf(t,d))
result.append(temp)
pd.DataFrame(result, columns=words)
➃ Observez les résultats du calcul IDF
#Calculer l'idf
result = []
for j in range(len(words)):
t = words[j]
result.append(idf(t))
pd.DataFrame(result, index=words, columns=["IDF"])
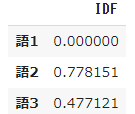
- Le coefficient $ idf $ pour le mot 1 qui apparaît dans les six documents est 0, et le mot 2 qui apparaît dans un seul document a la plus grande valeur de 0,778151.
➄ Calcul TF-IDF
#Calculer tfidf
result = []
for i in range(N):
temp = []
d = docs[i]
for j in range(len(words)):
t = words[j]
temp.append(tfidf(t,d))
result.append(temp)
pd.DataFrame(result, columns=words)
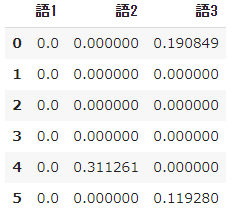
- $ Tfidf $ dans le mot 1 a un coefficient $ idf $ de 0, donc peu importe combien de fois il apparaît, il sera de 0.
- De plus, TF-IDF est un index proposé à l'origine à des fins de recherche d'informations, et pour les mots qui n'apparaissent même pas une seule fois, le dénominateur devient 0 (soi-disant division zéro) dans le calcul de $ idf $ et une erreur se produit. Ce sera.
⑷ Calcul par scikit-learn
- En réponse à ces problèmes, la bibliothèque TF-IDF de scikit-learn
TfidfVectorizerest implémentée avec une définition légèrement différente de la définition originale.
# scikit-apprendre TF-Importer la bibliothèque IDF
from sklearn.feature_extraction.text import TfidfVectorizer
- Calculons $ tfidf $ en utilisant
TfidfVectorizerpour la liste de données de mots des 6 documents ci-dessus.
#Liste unidimensionnelle
docs = [
"Mot 1 Mot 3 Mot 1 Mot 3 Mot 1",
"Mot 1 Mot 1",
"Mot 1 Mot 1 Mot 1",
"Mot 1 Mot 1 Mot 1 Mot 1",
"Mot 1 Mot 1 Mot 2 Mot 2 Mot 1",
"Mot 1 Mot 3 Mot 1 Mot 1"
]
#Générer un modèle
vectorizer = TfidfVectorizer(smooth_idf=False)
X = vectorizer.fit_transform(docs)
#Représenté dans un bloc de données
values = X.toarray()
feature_names = vectorizer.get_feature_names()
pd.DataFrame(values,
columns = feature_names)
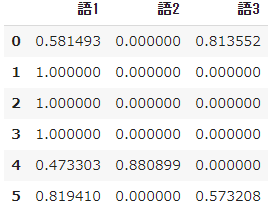
- $ Tfidf $ dans le mot 1 n'est plus 0 dans chaque document, et dans les mots 2 et 3, il a une valeur différente de la définition originale sauf pour les documents qui étaient à l'origine 0.
- Alors, reproduisons le résultat de scikit-learn basé sur la définition originale.
⑸ Reproduisez le résultat de scikit-learn
➀ Formule IDF modifiée
#Définition de la fonction idf
def idf(t):
df = 0
for doc in docs:
df += t in doc
#return np.log10(N/df)
return np.log(N/df)+1
- Modifiez
np.log10 (N / df)ennp.log (N / df) + 1 - En d'autres termes, changez le logarithme régulier avec la base 10 en logarithme naturel avec le nombre de base e et ajoutez +1.
#Calculer l'idf
result = []
for j in range(len(words)):
t = words[j]
result.append(idf(t))
pd.DataFrame(result, index=words, columns=["IDF"])
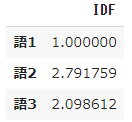
➁ Observez le résultat du calcul de TF-IDF
#Calculer tfidf
result = []
for i in range(N):
temp = []
d = docs[i]
for j in range(len(words)):
t = words[j]
temp.append(tfidf(t,d))
result.append(temp)
pd.DataFrame(result, columns=words)
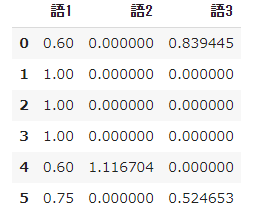
➂ Régularisation L2 des résultats des calculs TF-IDF
- Enfin, ** L2 régularise ** le résultat du calcul de $ tfidf $.
- Autrement dit, mettez les valeurs à l'échelle et convertissez-les de manière à ce qu'elles soient toutes au carré et additionnées à 1.
- La raison pour laquelle la régularisation est nécessaire est de compter le nombre de fois où chaque mot apparaît dans chaque document, mais comme chaque document a une longueur différente, plus le document est long, plus le nombre de mots a tendance à être grand.
- En supprimant l'effet du nombre total de ces mots, il est possible de comparer la fréquence d'occurrence des mots relativement.
#Calculer la valeur de la norme selon la définition uniquement dans le document 1 à titre d'essai
x = np.array([0.60, 0.000000, 0.839445])
x_norm = sum(x**2)**0.5
x_norm = x/x_norm
print(x_norm)
#Place-les et additionne-les pour s'assurer qu'ils sont 1
np.sum(x_norm**2)

- Profitons ici avec scikit-learn.
# scikit-Importer la bibliothèque de régularisation d'apprentissage
from sklearn.preprocessing import normalize
#Régularisation L2
result_norm = normalize(result, norm='l2')
#Représenté dans un bloc de données
pd.DataFrame(result_norm, columns=words)
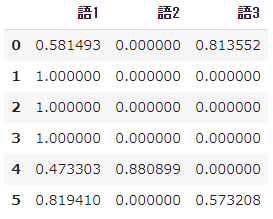
- En résumé, le TF-IDF de scikit-learn résout les deux inconvénients de la définition originale.
- Évitez zéro en utilisant le logarithme naturel dans la formule du coefficient $ idf $ et en ajoutant +1. À propos, la conversion de la logarithmique commune à la logarithmique naturelle est d'environ 2,303 fois.
- De plus, la régularisation L2 élimine l'effet de la différence du nombre de mots due à la longueur de chaque document.
- Le principe de TF-IDF est très simple, mais scikit-learn a divers paramètres, et il semble y avoir de la place pour un réglage en fonction de la tâche.
Recommended Posts