Génération de vecteurs de nombres aléatoires de haute dimension ~ Échantillonnage d'hypercube latin / Échantillonnage super carré latin ~

introduction

L'un des problèmes dans l'espace à haute dimension est le phénomène de concentration sphérique. Le phénomène de concentration sphérique est un phénomène dans lequel la densité de points augmente à la surface d'un supercube de dimension $ n $ dans un espace de grande dimension. Ce phénomène pose le problème que le nombre d'échantillons près du centre diminue lors de la recherche dans un espace de grande dimension ou en utilisant la méthode de Monte Carlo. Dans cet article, je voudrais présenter l'échantillonnage Latin Hypercube, qui est l'une des méthodes d'exemple pour résoudre ce problème. Il existe également une méthode d'échantillonnage bien connue utilisant la colonne Sobol.

Algorithme d'échantillonnage Latin Hypercube

Lors de l'échantillonnage de points $ M $ dans l'espace de dimension $ n $, l'échantillonnage d'hypercube latin divise d'abord chaque axe en grilles $ M $. Dans la figure ci-dessous, un exemple est donné lorsque $ n = 2 $ et $ M = 5 $.

Sélectionnez ensuite les cellules une par une afin que les lignes ne couvrent pas chaque colonne.

Des nombres aléatoires sont générés dans chaque cellule sélectionnée et utilisés comme points d'échantillonnage.

Cela empêchera la sélection de plus de quelques cellules qui se chevauchent, de sorte que la distance moyenne entre un point et le point le plus proche de l'espace sera probablement plus proche du centre de gravité de cellule à cellule (en fait différent, mais une image). En d'autres termes, l'image est qu'il est plus facile de voir l'espace plus uniformément avec moins d'échantillons. Par exemple, dans l'exemple bidimensionnel ci-dessus, le nombre total de carrés sur les bords (colonnes A, E, 1 ligne, 5 lignes) est de 16 et le nombre de carrés internes est de 9. Considérant une probabilité simple, la probabilité que tous les échantillons gèlent à l'extérieur

\frac{{}_{16} C _{5}}{{}_{25} C _{5}} = \frac{16 \times 15 \times 14 \times 13 \times 12}{25 \times 24 \times 23 \times 22 \times 21}=\frac{8 \times 13}{5 \times 23 \times 11} \simeq 8.2 \%

Il devient. D'autre part, l'échantillonnage d'hypercube latin échantillonne toujours à partir de chaque colonne et n'autorise pas la duplication de lignes, de sorte que la probabilité que tous les échantillons gèlent à l'extérieur est de 0 $ % $.

À propos, selon le calcul manuel à portée de main, lorsque $ n = 3, M = 5 $, il semble que tout soit solidifié à l'extérieur avec une probabilité de 29 $ % $ pour des nombres aléatoires uniformes et de 25,9 $ % $ pour l'échantillonnage d'hypercube latin. Il semble qu'il n'y ait pas beaucoup de différence si le nombre de divisions est petit. (Je ferai une expérience numérique plus tard.)

Code d'échantillonnage Latin Hypercube

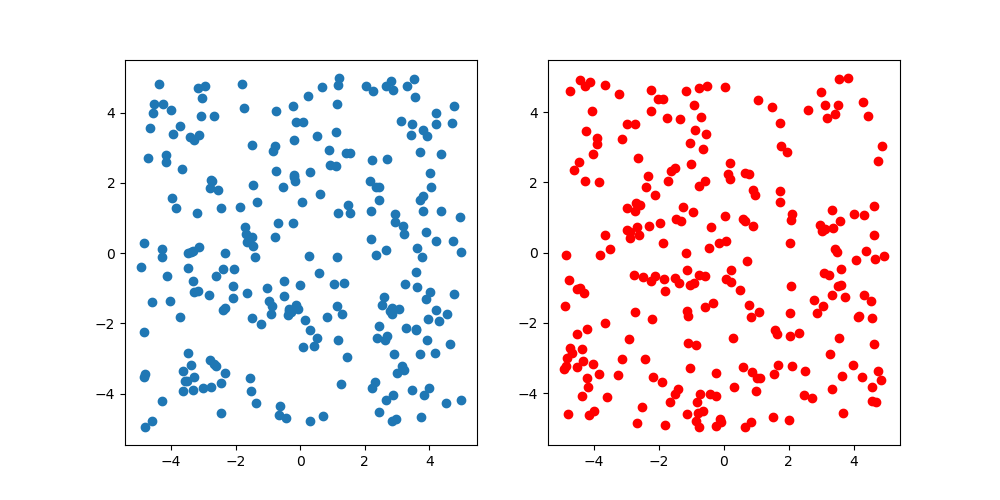
Juste au cas où, comparez avec un nombre aléatoire uniforme. Le nombre d'échantillons est de 250, le bleu est un nombre aléatoire uniforme et le rouge est l'échantillonnage Latin Hypercube. En regardant la figure, il ne semble pas qu'il y ait une telle différence, mais cela ne peut pas être aidé car elle est bidimensionnelle. Puisqu'il est difficile de visualiser des images de grande dimension, c'est la fin de cette vérification.

import numpy as np
import matplotlib.pyplot as plt 


n = 2
M = 250

lb, ub = -5., 5.

f = lambda x: (ub - lb) * x + lb
g = lambda x: (x - rng.uniform()) / M
rng = np.random.RandomState()
rs = f(rng.rand(M, n))

rnd_grid = np.array([rng.permutation(list(range(1, M + 1))) for _ in range(n)])
lhs = np.array([[f(g(rnd_grid[d][m])) for d in range(n)] for m in range(M)])


fig, ax = plt.subplots(1, 2, figsize=(10, 5)) 
ax[0].scatter(rs[:, 0], rs[:, 1]) 
ax[1].scatter(lhs[:, 0], lhs[:, 1], color="red")

plt.show()