Résumé de la génération de nombres aléatoires par Numpy
Le standard Python a également un module appelé random, mais numpy, qui peut effectuer des opérations vectorielles, s'exécute plus rapidement lors de "la génération d'un grand nombre de nombres aléatoires et l'exécution de certains traitements". Il existe également de nombreuses fonctions de distribution.
Nombre aléatoire uniforme
Générez un nombre aléatoire uniforme de 0 à 1 avec numpy.random.rand (). Plusieurs nombres aléatoires peuvent être générés en spécifiant un argument. Si vous souhaitez modifier la plage de nombres aléatoires, vous pouvez effectuer des opérations vectorielles ultérieurement.
from numpy.random import *
rand() #Générer un nombre aléatoire de 0 à 1
rand(100) #Génère 100 nombres aléatoires de 0 à 1
rand(10,10) #Générer une matrice 10x10 avec des nombres aléatoires de 0 à 1
rand(100) * 40 + 30 #Génère 100 nombres aléatoires de 30 à 70
Nombres aléatoires qui suivent une fonction de distribution particulière
N'importe quel nombre de nombres aléatoires peut être généré en spécifiant un argument tel que size = (10,10).
from numpy.random import *
"""Distribution normale standard. Soi-disant gaussien. Randn pour la distribution normale standard()Si vous souhaitez spécifier la moyenne / la variance, normal()Est utilisé."""
randn() #Distribution normale standard(Moyenne 0,Écart type 1)
randn(10) #Générer 10 distributions normales standard
randn(10,10) #Matrice 10x10 avec distribution normale standard
normal(50,10) #Distribution normale avec moyenne 50 et écart type 10
"""Distribution binaire. Le nombre de pièces qui peuvent être affrontées en lançant des pièces avec une probabilité de p n fois."""
binomial(n=100, p=0.5)
"""Distribution de Poisson. Distribution du nombre de fois où un phénomène qui se produit rarement est observé pendant une longue période. λ est la moyenne."""
poisson(lam=10) # λ=Distribution de Poisson de 10
"""Distribution bêta. Utilisé pour la distribution a priori conjuguée de la distribution binomiale."""
beta(a=3, b=5) # a=3, b=Distribution bêta de 5
Il existe de nombreuses autres distributions telles que la distribution χ, la distribution de Diricle, la distribution exponentielle, la distribution F, la distribution gamma, la distribution géométrique, la distribution de Gambel, la distribution supergéométrique, la distribution de Laplace, la distribution logistique, la distribution normale logarithmique, etc. Voir cette page pour plus de détails. http://docs.scipy.org/doc/numpy/reference/routines.random.html
entier
from numpy.random import *
randint(100) #Génère un entier de 0 à 99
randint(30,70) #Génère un entier de 30 à 69
randint(0,100,20) #Génère 20 entiers de 0 à 99
randint(0,100,(5,5)) #Générer une matrice 5x5 avec des entiers de 0 à 99
random_integers(100) #Génère un entier de 1 à 100
random_integers(30,70) #Génère un entier de 30 à 70
Extraction aléatoire de la liste
from numpy import *
city = ["Sapporo","Sendai","Tokyo","Nagoya","Kyoto","Osaka","Fukuoka"]
random.choice(city) #Extrayez-en un au hasard
random.choice(city,10) #Extraction aléatoire de 10 (avec duplication)
random.choice(city,5,replace=False) #Extraction aléatoire de 5 (pas de duplication))
#Lors de la pondération de la probabilité
weight = [0.1, 0.1, 0.3, 0.1, 0.1, 0.2, 0.1]
random.choice(city, p=weight) #Extrayez-en un avec la probabilité spécifiée
Initialisation de la génération de nombres aléatoires
Le nombre aléatoire généré par Numpy est un nombre pseudo aléatoire, donc si vous spécifiez une graine fixe, le même nombre aléatoire sera généré à chaque fois. Il est utilisé lorsque vous souhaitez que le même nombre aléatoire soit généré à chaque fois, par exemple lors du débogage.
from numpy.random import *
seed(100) #N'importe quel nombre est bien
rand() #Renvoie la même valeur à chaque fois
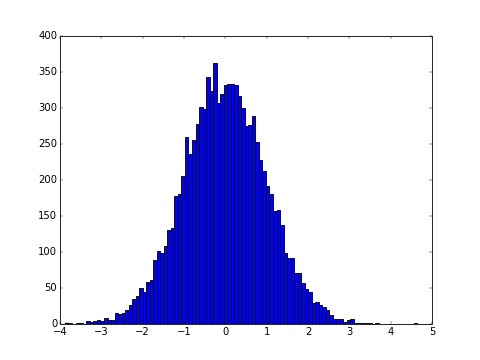
Vérifiez la distribution avec un histogramme
Si vous ne savez pas si les nombres aléatoires souhaités sont générés, il est conseillé de générer un grand nombre de nombres aléatoires et de dessiner un histogramme. Ici, un module de dessin de graphe appelé matplotlib est utilisé.
from numpy.random import *
import matplotlib.pyplot as plt
R = randn(10000) #Génère 10000 nombres aléatoires avec une distribution normale standard
plt.hist(R, bins=100) #Créez 100 histogrammes
plt.show() #Afficher le graphique
Application: génération de marche aléatoire
Générez une séquence aléatoire de droite ou de gauche, c'est-à-dire +1 ou -1, et prenez la somme cumulée cumsum ().
from numpy import *
L = 1000 #Nombre d'étapes
step = random.choice([-1,1],L) # +1 or -Générer L 1
position = cumsum(step) #Changement de poste

Recommended Posts