LSTM multivarié avec Keras
Je vois souvent des séries chronologiques univariées dans les keras, mais comme plusieurs facteurs sont impliqués dans la prédiction des prix des actions, des ventes, etc., cette fois, j'ai essayé de prédire en utilisant plusieurs données de séries chronologiques. ..
Introduction de la source
code
Basé sur le code introduit dans "MACHINE LEARNING MASTERY", il est compatible avec plusieurs variables. Time Series Prediction with LSTM Recurrent Neural Networks in Python with Keras
Cliquez ici pour le code complet qui peut être vu sur jupyter https://github.com/tizuo/keras/blob/master/LSTM%20with%20multi%20variables.ipynb
Les données
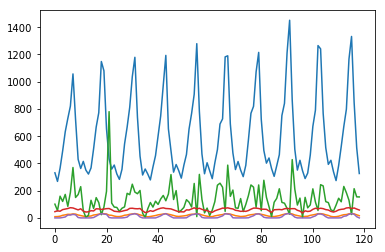
Des exemples de données sont empruntés à ce qui suit. Prédisez les ventes de glace les plus à gauche. Comment vendre de la glace
| ice_sales | year | month | avg_temp | total_rain | humidity | num_day_over25deg |
|---|---|---|---|---|---|---|
| 331 | 2003 | 1 | 9.3 | 101 | 46 | 0 |
| 268 | 2003 | 2 | 9.9 | 53.5 | 52 | 0 |
| 365 | 2003 | 3 | 12.7 | 159.5 | 49 | 0 |
| 492 | 2003 | 4 | 19.2 | 121 | 61 | 3 |
| 632 | 2003 | 5 | 22.4 | 172.5 | 65 | 7 |
| 730 | 2003 | 6 | 26.6 | 85 | 69 | 21 |
| 821 | 2003 | 7 | 26 | 187.5 | 75 | 21 |
Standardisation des données
Standardisez les données. Il a été expliqué que LSTM est sensible et que les nombres qu'il gère doivent être normalisés.
python
scaler = MinMaxScaler(feature_range=(0, 1))
dataset = scaler.fit_transform(dataset)
Données de test séparées
Cette fois, nous allons prédire les données de ce dernier demi-tiers, donc nous allons les séparer de celles pour l'apprentissage.
python
train_size = int(len(dataset) * 0.67)
test_size = len(dataset) - train_size
train, test = dataset[0:train_size,:], dataset[train_size:len(dataset),:]
Mise en forme des données
Étant donné que la valeur du mois suivant sera apprise en utilisant la valeur d'il y a jusqu'à 3 mois, formatez-la comme suit. Créez des variables qui l'utilisent et stockez-les dans les données à un moment donné.
| Y | il y a 3 mois | il y a 2 mois | Il ya 1 mois |
|---|---|---|---|
| Valeur de janvier | Valeur d'octobre | 1Valeur de janvier | Valeur de décembre |
| Valeur de février | Valeur de novembre | 1Valeur de février | Valeur de janvier |
| Valeur de mars | Valeur de décembre | Valeur de janvier | Valeur de février |
Cette fois, nous le considérons comme un ensemble par an et l'analyse rétrospective crée des données avec 12.
python
def create_dataset(dataset, look_back=1):
dataX, dataY = [], []
for i in range(len(dataset)-look_back-1):
xset = []
for j in range(dataset.shape[1]):
a = dataset[i:(i+look_back), j]
xset.append(a)
dataY.append(dataset[i + look_back, 0])
dataX.append(xset)
return numpy.array(dataX), numpy.array(dataY)
look_back = 12
trainX, trainY = create_dataset(train, look_back)
testX, testY = create_dataset(test, look_back)
Convertissez ces données dans un format accepté par keras LSTM. [Nombre de lignes]> [Nombre de variables]> [Nombre de colonnes (nombre de recherches)]
python
trainX = numpy.reshape(trainX, (trainX.shape[0], trainX.shape[1], trainX.shape[2]))
testX = numpy.reshape(testX, (testX.shape[0], testX.shape[1], testX.shape[2]))
La modélisation
input_shape contient le nombre de variables et le nombre de recherches. Le nombre de sorties est fixé à 4 comme dans l'échantillon sans le prendre en compte.
python
model = Sequential()
model.add(LSTM(4, input_shape=(testX.shape[1], look_back)))
model.add(Dense(1))
model.compile(loss='mean_squared_error', optimizer='adam')
model.fit(trainX, trainY, epochs=1000, batch_size=1, verbose=2)
Vérification
La prédiction est la même que d'habitude.
python
trainPredict = model.predict(trainX)
testPredict = model.predict(testX)
Après cela, renvoyez Y au nombre non standardisé. Étant donné que la mise à l'échelle n'est acceptée que si elle a la même forme que l'ensemble de données d'origine, la valeur est remplie avec 0 pour le nombre de colonnes qui existaient. S'il vous plaît laissez-moi savoir s'il existe un moyen plus intelligent.
python
pad_col = numpy.zeros(dataset.shape[1]-1)
def pad_array(val):
return numpy.array([numpy.insert(pad_col, 0, x) for x in val])
trainPredict = scaler.inverse_transform(pad_array(trainPredict))
trainY = scaler.inverse_transform(pad_array(trainY))
testPredict = scaler.inverse_transform(pad_array(testPredict))
testY = scaler.inverse_transform(pad_array(testY))
Enfin, l'écart type est donné.
python
trainScore = math.sqrt(mean_squared_error(trainY[:,0], trainPredict[:,0]))
print('Train Score: %.2f RMSE' % (trainScore))
testScore = math.sqrt(mean_squared_error(testY[:,0], testPredict[:,0]))
print('Test Score: %.2f RMSE' % (testScore))
Après avoir changé le nombre de variables, il est devenu comme suit. Bien sûr, vous devez choisir la variable à lancer.
| Un modèle appris uniquement des ventes de glaces | Glace et 25 degrés ou plus jours | Tout | |
|---|---|---|---|
| Train Score | 30.20 RMSE | 15.19 RMSE | 8.44 RMSE |
| Test Score | 111.97 RMSE | 108.09 RMSE | 112.90 RMSE |

Recommended Posts