Analyse en composants principaux (PCA) et analyse en composants indépendants (ICA) avec python
introduction
Lors de l'analyse des données d'ondes cérébrales (EEG) et d'encéphalogrammes (MEG) dans la recherche, nous avons décidé d'utiliser PCA et ICA pour décomposer les composants de l'activité cérébrale et analyser les résultats de la réduction de dimension en tant que quantités de caractéristiques. Pour être honnête, je ne suis pas sûr du contexte mathématique, mais pour le moment, j'ai résumé l'APC et l'ICA des données de séries chronologiques sous forme de mémorandum sur la base de la mise en œuvre.
- J'espère ajouter une formation mathématique plus tard.
Analyse en composantes principales (ACP) et analyse en composantes indépendantes (ICA)
Qu'est-ce que le PCA
Wikipédia Que,
- L'analyse en composantes principales (ACP) est une analyse multivariée qui synthétise une variable appelée la composante principale qui représente le mieux la variation globale avec un petit nombre de variables non corrélées à partir d'un grand nombre de variables corrélées. Une méthode. Utilisé pour réduire la dimension des données. La transformation qui donne le composant principal est choisie de manière à maximiser la dispersion du premier composant principal et maximiser la dispersion sous la contrainte que les composants principaux suivants sont orthogonaux aux composants principaux déterminés précédemment. *
En d'autres termes ** Lorsqu'on peut supposer que les données suivent une distribution normale, la méthode consistant à prendre l'axe dans la direction orthogonale dans l'ordre à partir de la composante avec la plus grande dispersion Puisque les bases sont orthogonales, les sorties sont des données non corrélées entre elles (il n'y a pas de relation linéaire, mais il peut y avoir une relation non linéaire) **
Qu'est-ce que l'ICA
[Wikipédia](https://ja.wikipedia.org/wiki/%E7%8B%AC%E7%AB%8B%E6%88%90%E5%88%86%E5%88%86%E6%9E À partir de% 90, "Wikipédia")
- L'analyse des composants indépendants (ICA) est une méthode de calcul permettant de séparer les signaux multivariés en plusieurs composants additifs. Chaque composant suppose un signal non gaussien qui est statistiquement indépendant l'un de l'autre. Il s'agit d'un cas particulier de séparation aveugle du signal. *
En d'autres termes ** Une méthode qui s'axe dans le sens de l'indépendance maximale quand on peut supposer que les données sont statistiquement indépendantes et ne suivent pas une distribution normale. La sortie sera des données indépendantes qui ne suivent pas une distribution normale (pas de relations linéaires ou non linéaires) **
Différence entre PCA et ICA (image)
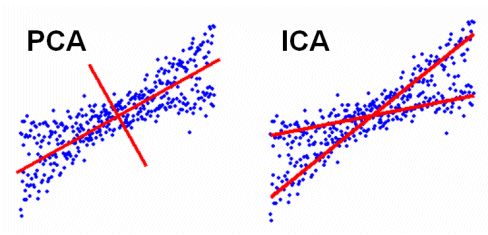 (Référence http://meg.aalip.jp/ICA/)
(Référence http://meg.aalip.jp/ICA/)
Implémentation PCA
PCA.py
import numpy as np
import matplotlib.pyplot as plt
from sklearn.decomposition import PCA
X = input_data #400 (nombre de données) x 300 (série chronologique) données
#Exécutez PCA
pca = PCA(n_components=20, random_state=0)#Faire 20 bases (composants)
feature = pca.fit_transform(X)
PCA_comp = pca.components_ #Matrice de base
#Restaurer les 0èmes données en utilisant 20 composants
plt.figure(figsize = (12, 2))
plt.plot(X[0], label="data")#0ème donnée
plt.plot(np.dot(feature[0], PCA_comp).T, label="reconstruct")#0ème donnée restaurée
plt.legend()

Implémentation ICA
ICA.py
import numpy as np
import matplotlib.pyplot as plt
from sklearn.decomposition import FastICA
X = input_data #400 (nombre de données) x 300 (série chronologique) données
#Mise en œuvre de l'ICA
ICA = FastICA(n_components=20, random_state=0)#Faire 20 bases (composants)
X_transformed = ICA.fit_transform(X)
A_ = ICA.mixing_.T #Matrice mixte
#Restaurer les 0èmes données en utilisant 20 composants
plt.figure(figsize = (12, 2))
plt.plot(X[0], label="data")#0ème donnée
plt.plot(np.dot(X_transformed[0], A_), label="reconstruct")#0ème donnée restaurée
plt.legend()

en conclusion
Cette fois, j'ai résumé le PCA et l'ICA dans un mémorandum. Je pensais que ce serait bien parce que j'ai pu l'implémenter pour le moment, mais je pense que j'ai besoin d'acquérir plus de connaissances théoriques pour l'avenir. Je voudrais ajouter à propos de NMF (Non-Negative Matrix Factor Decomposition).
référence
・ Méthode de réduction de dimension (résumé et mise en œuvre) PCA, LSI (SVD), LDA, ICA
Recommended Posts