[Apprentissage automatique] Qu'est-ce que la norme LP?

En étudiant l'apprentissage automatique, je pense que les termes régularisation L1 et régularisation L2 apparaissent. [^ 1]

[^ 1]: "Blog des Data Scientists travaillant à Ginza" de TJO Pratiquez la régularisation L1 / L2 dans R Est également repris.

Terme de pénalité pour la régularisation L1: la norme L1 ressemble à ceci,

Pénalité pour la régularisation L2: la norme L2 ressemble à ceci,

Explorons un peu plus en profondeur pourquoi les normes L1 et L2 sont représentées de cette manière.

Définition de la norme Lp

Vecteur $ {\ bf x} $ en n dimensions,

{\bf x} = (x_1, \cdots, x_n)

Alors la norme $ L ^ p $ est définie comme:

\| {\bf x} \|_p = (\ |x_1|^p + |x_2|^p + \cdots + |x_n|^p )^{1/p}

Norme L1

Ici, la norme $ L ^ 1 $ lorsque $ {\ bf x} $ est bidimensionnelle pour pouvoir être dessinée dans le graphe est

\| {\bf x} \|_1 = |x_1| + |x_2|

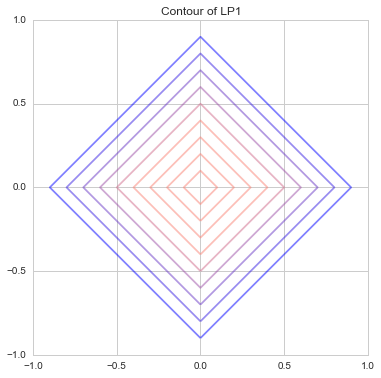
C'est juste l'addition des valeurs absolues de $ x_1 $ et $ x_2 $. Celui qui le représente avec des courbes de niveau C'était comme ça. Cela s'appelle également [Manhattan Distance](https://ja.wikipedia.org/wiki/Manhattan Distance), et comme il n'y a que des routes verticales verticales et horizontales comme une grille, seul un mouvement vertical ou horizontal est possible, et il se déplace en diagonale. C'est le même que celui qui représente la distance du monde que vous ne pouvez pas faire. En d'autres termes, comme ceci, les lignes bleu clair, rouge et verte ont toutes une longueur de 10, donc si vous connectez la même distance avec une ligne, ce sera une ligne droite comme celle-ci. Les courbes de niveau dans le graphique ci-dessus sont donc en forme de losange, n'est-ce pas?

Norme L2

De même, la norme $ L ^ 2 $ du vecteur bidimensionnel est

\| {\bf x} \|_2 = \sqrt{|x_1|^2 + |x_2|^2}

est. C'est la distance euclidienne familière. Comme la distance de l'origine du point sur la circonférence est toujours constante, elle devient une ligne de contour qui dessine un beau cercle comme indiqué ci-dessous.

Normes à divers ps

Les normes L1 et L2 sont souvent utilisées dans l'apprentissage automatique, mais dans un souci de compréhension, j'ai essayé de voir quelles courbes de niveau sont dessinées avec différentes valeurs p.

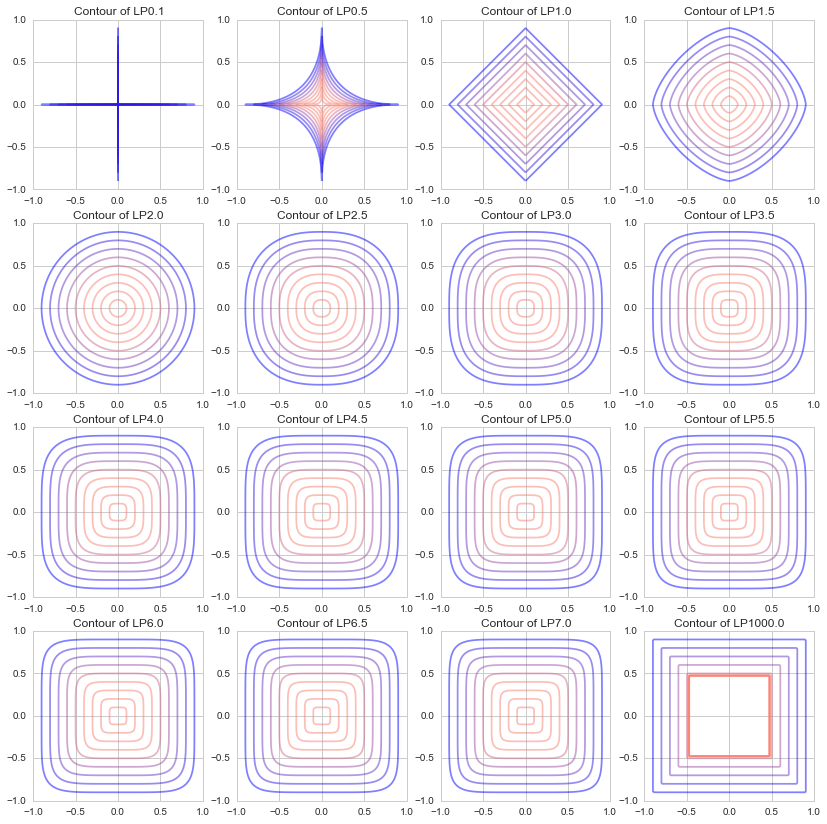
J'ai dessiné un diagramme de $ p = 1000 $, avec 0,5 $ chacun de $ p = 0,1, \ p = 0,5 à 7,5 $. (À l'origine, $ p $ dans la norme Lp est un nombre réel de $ p \ ge1 $, mais j'ai osé dessiner 0,1 et 0,5.)

Il s'avère que lorsque p s'approche de 0, il devient une forme comme "+", quand il vaut 1, il devient un losange (un carré pivoté de 45 degrés), quand il s'approche de 2, il devient un cercle, et quand il s'approche de ∞, il devient une forme comme "□". Je vais.

(Bien que ce soit en dehors de la définition de la norme Lp, s'il y a un monde avec p = 0,1, c'est un monde très difficile à faire en diagonale: sweat_smile :)

Ces normes L1 et L2 sont appliquées et utilisées dans la régression Lasso, la régression Ridge, ElasticNet, etc.: kissing_closed_eyes:

Code Python @GitHub

Le code de la partie principale de cet article est ci-dessous.

def LP(x, y, lp=1):
    x = np.abs(x) 
    y = np.abs(y)
    return (x**lp + y**lp)**(1./lp)

def draw_lp_contour(lp=1, xlim=(0, 1), ylim=(0, 1)):
    n = 201
    X, Y = np.meshgrid(np.linspace(xlim[0], xlim[1], n), np.linspace(ylim[0], ylim[1], n))
    Z = LP(X, Y, lp) 
    cm = generate_cmap(['salmon', 'salmon', 'salmon', 'salmon', 'blue'])
    interval = [i/10. -1 for i in range(20)]
    
    plt.contour(X, Y, Z, interval, alpha=0.5, cmap=cm)
    plt.title("Contour of LP{}".format(lp))
    plt.xlim(xlim[0], xlim[1])
    plt.ylim(ylim[0], ylim[1])

#Tracez un graphique de 16 types de valeurs p
fig =plt.figure(figsize=(14,14))
size = 4
for i, lp in enumerate(np.r_[[0.1], np.linspace(0.5, 7, 14), [1000]]):
    plt.subplot(size, size, i+1)
    draw_lp_contour(lp, (-1, 1),(-1, 1))

Le texte complet du code Python qui a dessiné ce graphique peut être trouvé sur GitHub. https://github.com/matsuken92/Qiita_Contents/blob/master/General/LP-Norm.ipynb

référence

Wikipédia Lp espace https://ja.wikipedia.org/wiki/Lp空間

Apprentissage automatique en ligne (série professionnelle d'apprentissage automatique) [Umino, Okanohara, Tokui, Tokunaga] 　http://www.kspub.co.jp/book/detail/1529038.html

Pratiquer la régularisation L1 / L2 en R 　http://tjo.hatenablog.com/entry/2015/03/03/190000

Effet de la régularisation L1 et de la régularisation L2 sur le modèle de régression 　http://breakbee.hatenablog.jp/entry/2015/03/08/041411