Analyse des séries chronologiques n ° 6 Faux retour et partie républicaine
1. Vue d'ensemble
- Dans la continuité de la Partie 5, j'étudie sur la base de «l'analyse des séries chronologiques de mesure des données économiques et financières».
- Cet article concerne le retour apparent et la partie républicaine du chapitre 6.
2. Faux retour
Définition
Il semble y avoir une relation significative entre $ x_t $ et $ y_t $ lors du retour de $ y_t = \ alpha + \ beta x_t + \ epsilon_t $ pour deux processus racine unitaires non liés $ x_t $ et $ y_t $ Le phénomène qui ressemble s'appelle un faux retour.
Vérification
- Deux processus indépendants
$ \ qquad x_t = x_ {t-1} + \ epsilon_ {x, t}, \ quad \ epsilon_ {x, t} \ sim iid (0, \ sigma_x ^ 2) $
$ \ qquad y_t = y_ {t-1} + \ epsilon_ {y, t}, \ quad \ epsilon_ {y, t} \ sim iid (0, \ sigma_y ^ 2) $
$ \ qquad y_t = \ alpha + \ beta x_t + \ epsilon_t $
Revenir au modèle.
#Génération de données
sigma_x, sigma_y = 1, 2
T = 10000
xt = np.cumsum(np.random.randn(T) * sigma_x).reshape(-1, 1)
yt = np.cumsum(np.random.randn(T) * sigma_y).reshape(-1, 1)
- Une fois tracé, il ressemble à ce qui suit.
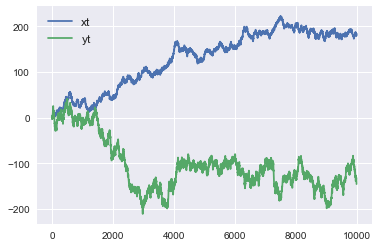
- Tout d'abord, nous avons effectué une régression avec scicit-learn.
from sklearn.linear_model import LinearRegression
reg = LinearRegression().fit(xt,yt)
print('R-squared : ',reg.score(xt,yt))
print('coef : ',reg.coef_, 'intercept', reg.intercept_)
R-squared : 0.4794854506874714
coef : [[-0.62353254]] intercept [-24.27600549]
- Le coefficient de décision ($ R ^ 2 $) était de 0,479, ce qui était une valeur assez élevée. Pour le modèle de régression, il était sous la forme $ \ alpha = -24,28, \ quad \ beta = -0,6235 $.
- Pour tester si $ x_t $ et $ y_t $ sont indépendants, nous voulons tester $ H_0: \ beta = 0 $. Cependant, je n'ai pas pu trouver une telle fonction dans scicit-learn.
- Quand j'ai cherché d'autres bibliothèques, les statsmodels me semblaient utiles, donc je suis retourné avec des statsmodels.
import statsmodels.api as sm
reg = sm.OLS(yt,sm.add_constant(xt,prepend=False)).fit()
reg.summary()
|
|
|
|
| Dep. Variable: |
y |
R-squared: |
0.479 |
| Model: |
OLS |
Adj. R-squared: |
0.479 |
| Method: |
Least Squares |
F-statistic: |
9210. |
| Date: |
Tue, 07 Jan 2020 |
Prob (F-statistic): |
0.00 |
| Time: |
22:36:57 |
Log-Likelihood: |
-51058. |
| No. Observations: |
10000 |
AIC: |
1.021e+05 |
| Df Residuals: |
9998 |
BIC: |
1.021e+05 |
| Df Model: |
1 |
|
|
| Covariance Type: |
nonrobust |
|
|
|
coef |
std err |
t |
P>abs(t) |
[0.025 |
0.975] |
| const |
-24.2760 |
0.930 |
-26.113 |
0.000 |
-26.098 |
-22.454 |
| x1 |
-0.6235 |
0.006 |
-95.968 |
0.000 |
-0.636 |
-0.611 |
- add_constant est lié à l'opportunité d'inclure un terme constant ($ \ alpha $ dans l'équation de régression précédente) dans le modèle de régression. En faisant add_constant, le terme constant sera inclus dans le modèle de régression. Dans le cas de scicit-learn, si l'argument fit_intercept est défini sur False, la régression n'aura pas de terme constant. Ceci n'est pas spécifié ci-dessus, car fit_intercept = True est la valeur par défaut.
- Comme pour scikit-learn, les coefficients de détermination étaient de 0,479, $ \ alpha = -24,28, \ quad \ beta = -0,6235 $, confirmant qu'une régression équivalente a été obtenue.
- L'avantage des statsmodels est qu'ils vous donnent 95% de valeurs significatives. En regardant cela, pour $ H_0: \ beta = 0 $, $ H_0 $ sera rejeté car il doit être compris entre -0,636 et -0,611 au niveau de signification de 95%. C'est un faux retour.
Comment éviter
Inclure les variables de retard dans le modèle
- Modifiez le modèle à renvoyer comme suit.
$ \ qquad y_t = \ alpha + \ beta_1 x_t + \ beta_2 y_ {t-1} + \ epsilon_t $
$ y_ {t-1} $ est ajouté aux variables explicatives de $ y_t $.
Lors du retour en utilisant des modèles de statistiques, cela devient comme suit. sm.OLS prend des variables expliquées et des variables explicatives comme arguments, mais il est nécessaire d'alimenter les variables explicatives ensemble dans un tableau comme indiqué ci-dessous.
x_t, y_t, y_t_1 = xt[1:], yt[1:], yt[:-1]
X = np.column_stack((x_t, y_t_1))
reg = sm.OLS(y_t,sm.add_constant(X)).fit()
reg.summary()
|
|
|
|
| Dep. Variable: |
y |
R-squared: |
0.999 |
| Model: |
OLS |
Adj. R-squared: |
0.999 |
| Method: |
Least Squares |
F-statistic: |
3.712e+06 |
| Date: |
Thu, 09 Jan 2020 |
Prob (F-statistic): |
0.00 |
| Time: |
22:12:59 |
Log-Likelihood: |
-21261. |
| No. Observations: |
9999 |
AIC: |
4.253e+04 |
| Df Residuals: |
9996 |
BIC: |
4.255e+04 |
| Df Model: |
2 |
|
|
| Covariance Type: |
nonrobust |
|
|
|
coef |
std err |
t |
P>abs(t) |
[0.025 |
0.975] |
| const |
-0.0815 |
0.049 |
-1.668 |
0.095 |
-0.177 |
0.014 |
| x1 |
-0.0004 |
0.000 |
-0.876 |
0.381 |
-0.001 |
0.000 |
| x2 |
0.9989 |
0.001 |
1964.916 |
0.000 |
0.998 |
1.000 |
- Dans le modèle précédent, le résultat était $ \ alpha = -0,0815, \ quad \ beta_1 = -0,0004, \ quad \ beta_2 = 0,9899 $. $ \ Alpha $ et $ \ beta_1 $ valent presque 0, dont la plupart peuvent être expliqués par $ y_ {t-1} $. Et le coefficient de corrélation est de 0,999, ce qui est aussi proche que possible de 1. Notez également que $ H_0: \ beta_1 = 0 $ n'est pas rejeté.
Prenez la différence du processus de racine de l'unité et faites-en un processus régulier avant de revenir
- Modifiez le modèle à renvoyer comme suit.
$ \ qquad \ Delta y_t = \ alpha + \ beta \ Delta x_t + \ epsilon_t $
x_t, y_t = np.diff(xt.flatten()).reshape(-1,1), np.diff(yt.flatten()).reshape(-1,1)
reg = sm.OLS(y_t,sm.add_constant(x_t)).fit()
reg.summary()
|
|
|
|
| Dep. Variable: |
y |
R-squared: |
0.000 |
| Model: |
OLS |
Adj. R-squared: |
0.000 |
| Method: |
Least Squares |
F-statistic: |
3.297 |
| Date: |
Thu, 09 Jan 2020 |
Prob (F-statistic): |
0.0694 |
| Time: |
22:33:26 |
Log-Likelihood: |
-21262. |
| No. Observations: |
9999 |
AIC: |
4.253e+04 |
| Df Residuals: |
9997 |
BIC: |
4.254e+04 |
| Df Model: |
1 |
|
|
| Covariance Type: |
nonrobust |
|
|
| coef |
std err |
t |
P>abs(t) |
[0.025 |
0.975] |
| const |
-0.0138 |
0.020 |
-0.681 |
0.496 |
-0.054 |
| x1 |
-0.0374 |
0.021 |
-1.816 |
0.069 |
-0.078 |
- Dans ce cas, le coefficient de corrélation est de 0, soit presque 0 à $ \ beta = -0,0374 $. Il n'est pas non plus possible de rejeter $ H_0: \ beta_1 = 0 $, conduisant à la conclusion qu'il n'y a pas de relation significative entre $ \ Delta x_t $ et $ \ Delta y_t $.
3. Kyowa
Définition
- Soit $ x_t $ et $ y_t $ le processus racine unitaire ($ \ rm I (1) $). A ce moment, quand il y a $ a $ et $ b $ qui sont des processus stationnaires tels que $ a x_t + by_t \ sim \ rm I (0) $, il y a une relation républicaine entre $ x_t $ et $ y_t $. Il y a. De plus, $ (a, b) '$ est appelé un vecteur républicain.
- Plus généralement, pour $ \ mathbb y_t \ sim \ rm I (1) $, il existe $ \ mathbb a $ tel que $ \ mathbb a '\ mathbb y_t \ sim \ rm I (0) $ Lorsque vous le faites, $ \ mathbb y_t $ a une relation républicaine. De plus, $ \ mathbb a $ est appelé un vecteur républicain.
- Par exemple, $ u_ \ {1t}, u_ \ {2t} $ est un processus stationnaire indépendant et $ w_ \ {1t}, w_ \ {2t} $ est un processus racine unitaire indépendant.
$ \ qquad \ left \ {\ begin {array} {ll} x_t = \ alpha w_ \ {1t} + u_ \ {1t} \\ y_t = \ beta w_ \ {1t} + u_ \ {2t} \ end { Considérez le tableau} \ right. $
. À ce stade, $ x_t $ et $ y_t $ sont des processus $ \ rm I (1) $, mais
$ \ qquad x_t- \ frac {\ alpha} {\ beta} y_t = u_ {1t} - \ Depuis frac {\ alpha} {\ beta} u_ {2t} \ sim \ rm I (0) $
, il existe une relation républicaine entre $ x_t $ et $ y_t $, et le vecteur républicain est . (1, - \ frac {\ alpha} {\ beta}) '.
Implication
- Lorsque $ x_t $ et $ y_t $ sont des processus racine unitaire, l'erreur de prédiction à long terme de $ x_t $ et $ y_t $ devient grande.
- Cependant, s'il y a une relation républicaine entre $ x_t $ et $ y_t $, alors il existe $ a $ tel que $ z_t = y_t --a x_t $ est un processus régulier, auquel cas $ z_t $ est à long terme. Il est possible de faire des prédictions précises avec un certain degré de précision.
Théorème d'expression de Granger
- Un modèle VAR qui inclut une relation républicaine peut être représenté par un modèle de correction d'erreur vectorielle (VECM).
- Pour le système républicain $ \ mathbb y_t $ avec représentation VAR (p),
$ \ qquad \ begin {align} \ Delta \ mathbb y_t & = \ zeta_1 \ Delta \ mathbb y_ {t-1} + \ zeta_2 \ Delta \ mathbb y_ {t-2} + \ cdots + \ zeta_ {p-1} \ Delta \ mathbb y_ {t-p + 1} + \ mathbb \ alpha + \ zeta_0 \ Delta \ mathbb y_ {t- 1} + \ epsilon_t \\ & = \ zeta_1 \ Delta \ mathbb y_ {t-1} + \ zeta_2 \ Delta \ mathbb y_ {t-2} + \ cdots + \ zeta_ {p-1} \ Delta \ mathbb y_ {t-p + 1} + \ mathbb \ alpha + - \ mathbb B \ mathbb A '\ mathbb y_ {t-1} + \ epsilon_t \ end {align} $
avec VECM (p-1) Peut être exprimé.
- $ - \ mathbb B \ mathbb A '\ mathbb y_ {t-1} $ est appelé le terme de correction d'erreur. Ici, $ \ mathbb A $ représente le vecteur républicain, et le terme de correction d'erreur indique que la force de retour à l'équilibre fonctionne lorsque l'écart par rapport à l'équilibre devient important.
