Chainer and deep learning learned by function approximation
Let's learn chainer through the theme of learning the function $ y = e ^ x $ by so-called deep learning. The following is confirmed with chainer 1.6.2.1.
The same content is placed in Jupyter notebook format here, so if you want to check it while moving, please refer to that.
First, import the required modules.
import numpy as np
import chainer
from chainer import cuda, Function, gradient_check, Variable, optimizers, serializers, utils
from chainer import Link, Chain, ChainList
import chainer.functions as F
import chainer.links as L
from matplotlib import pyplot as plt
%matplotlib inline
Creation of teacher data
First, create a function that outputs teacher data. This time, $ e ^ x $ is the expected value for the floating point $ x $ from 0 to 1.0.
We use a technique called batch learning, but it is convenient to have a function that returns a set of $ n $ questions and answers.
def get_batch(n):
x = np.random.random(n)
y = np.exp(x)
return x,y
print get_batch(2)
(array([ 0.25425583, 0.87356596]), array([ 1.28950165, 2.39543768]))
Neural network design
Next, design the neural network.
Since $ y = e ^ x $ is a non-linear function, approximation with linear functions alone does not provide sufficient accuracy. When the input is $ x $, something like $ y = Wx + b $ is called a linear function. $ W $ is called a weight and $ b $ is called a bias, both of which are just matrices. In other words, it's a straight line (like).
By the way, for this linear operation, it seems that it can be called a neural network just by adding an activation layer by a nonlinear function. A multi-layered version of this is a deep neural network, a non-linear function used in so-called deep learning. I don't know how deep it should be called deep, but this time I'll try about 3 steps.
A non-linear function called relu is very often used for general classification problems, but leaky_relu is used this time because relu loses its derivative (in this case, relu did not converge). .. leaky_relu is a simple function that just multiplies 0.2 if the input is negative.
By optimizing the parameters $ W and b $ of each linear layer, we will try to express a function that corresponds to $ y = e ^ x $.
So, let's configure the neural network as follows. L1, L2, and L3 are linear functions, respectively. After increasing the dimensions of the intermediate layer $ h1 and h2 $ to 16 and 32, they are finally dropped to one dimension.

In the following, the parameters $ W, b $ of $ L_n $ are expressed as $ W_n, b_n $.
The fact that the middle layer (hidden layer) $ h1 and h2 $ can have many channels (that is, the matrix of parameters $ W_n and b_n $ is huge) shows the expressive power of the network. If there are no non-linear elements in the middle,
\begin{eqnarray*}
h_3 &=& W_3 (W_2(W_1x+b_1)+b_2)+b_3 \\
&=& W_3 W_2 W_1 x + W_3W_2b_1 + W_3b_2 + b_3 \\
&=& W x + b
\end{eqnarray*}
It will be. $ W = W_3 W_2 W_1, b = W_3 W_2b_1 + W_3b_2 + b_3 $, but no matter how large the matrix such as $ W_1, W_2, W_3 $ is, the parameters $ W and b $ of the composition function are both. It will be a scalar. The fact that $ x, W, b $ are all scalars means that $ y = Wx + b $ is a straight line that can change only the slope and intercept, and fit this to $ e ^ x $. It's impossible. However, all the parameters of $ W_1, W_2, W_3 $ will live just by inserting the non-linear element. This is the reason why I mentioned at the beginning, "If there is a non-linear element, you can call it a neural network."
Neural net implementation
Write this down with chainer.
In chainer, functions with parameters to be optimized are called L (link), and functions without parameters are called F (function) to distinguish them. It seems that this area is a concept introduced from around ver1.5, and I often see tutorials that write links with functions. Links are defined starting with uppercase letters, such as L.Linear (input size, output size), and functions are defined starting with lowercase letters, such as F.linear (x, W, b). Older versions seem to have used functions that start with a capital letter, including F.Linear (), L.Linear (), and F.linear (). The former two are equivalent and parameterized functions, and the last is just a function that gives parameters. I was a little confused before I understood this.
The story was a little off. Next, pass a collection of links to create a class called a chain. If you're not familiar with how to write Python classes, you'll be annoyed, but all you need is \ _ \ _ init \ _ \ _ () to define the link list and a function that returns a computational graph to the output. Here, we will return the loss as \ _ \ _ cal \ _ \ _ (). The function defined by \ _ \ _ call \ _ \ _ () is
m=MyChain()
loss=m(x,t)
You can call it like this.
The point is that the function including the parameter is separated into \ _ \ _ init \ _ \ _ (), and the others are separated so that they can be used in \ _ \ _ call () \ _ \ _ and other methods. L.Linear () is much easier to write than TensorFlow because you only need to pass the number of input channels and output channels as parameters.
class MyChain(Chain):
def __init__(self):
super(MyChain, self).__init__(
l1=L.Linear(1, 16), #1 input channel, 16 output channels
l2=L.Linear(16, 32),
l3=L.Linear(32, 1),
)
def __call__(self,x,t):
#Returns the difference between the network output when x is entered and the answer t.
#This time we will use the mean square error.
return F.mean_squared_error(self.predict(x),t)
def predict(self,x):
#Returns the network output when x is entered.
h1 = F.leaky_relu(self.l1(x))
h2 = F.leaky_relu(self.l2(h1))
h3 = F.leaky_relu(self.l3(h2))
return h3
def get(self,x):
#This is a convenient function that inputs x as a real number and returns the output as a real number.
# numpy.It's a little confusing because it goes through ndarray and Variable.
return self.predict(Variable(np.array([x]).astype(np.float32).reshape(1,1))).data[0][0]
Instantiate this model and configure the optimizer to optimize the parameters according to your specific strategy. This time I will use something called Adam ().
model = MyChain()
optimizer = optimizers.Adam()
optimizer.setup(model)
Learning
Finally, we will turn the learning loop.
As a chainer method, a multidimensional array (tensor) of np.float32 with a dimensional structure (batch axis, data axis 1, (data axis 2), ..) is converted into a Variable class and exchanged. Use the data method to retrieve a numeric entity from the Variable class. ... I don't understand at all when I write it.
A batch is a sampling of some from the teacher data. Is it easier to understand the number of batches as the number of samples? The parameters are always updated for multiple sample numbers, but a multidimensional array (tensor) is handled, in which a dimension called the number of data channels is added, and then the dimensions required for data representation are added. It will be.
In this case, the input data is one-dimensional, so (Batch axis, data axis) Is fine, but the data composed of RGB3 channels of 2D images is (Batch axis, channel axis = color axis, vertical axis, horizontal axis) Pass like. It's hard to understand unless you get used to it. I have an image like the one below.
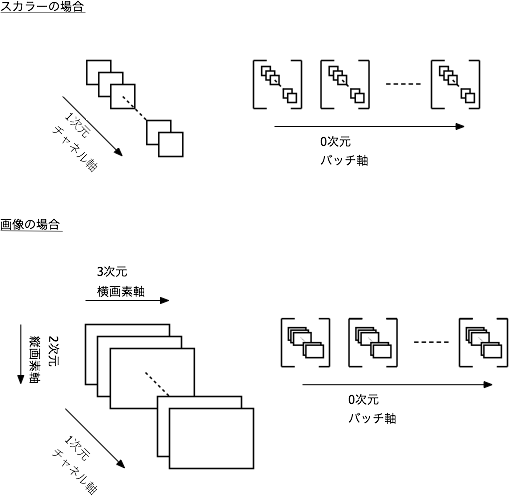
Learning updates
- Initialization of differentiation
- Forward propagation (following the net forward to calculate the output, in this case model (x \ _, t \ _))
- Backward propagation (calculates the derivative of the parameter by tracing the net in the opposite direction)
- Optimizer update (update parameters using differentiation)
Is a series of flows. optimizer.update (model) will do this at once, but I often want to see the progress of forward, so I often write everything as follows.
losses =[]
for i in range(10000):
x,y = get_batch(100)
x_ = Variable(x.astype(np.float32).reshape(100,1))
t_ = Variable(y.astype(np.float32).reshape(100,1))
model.zerograds()
loss=model(x_,t_)
loss.backward()
optimizer.update()
losses.append(loss.data)
plt.plot(losses)
plt.yscale('log')

The horizontal axis is the number of loops, and the vertical axis is the log plot of loss. It's been reduced to a good feeling.
Check the result
Now, let's check the output of the completed model. If you enter 0.2, will you get a value close to exp (0.2)?
print model.get(0.2)
print np.exp(0.2)
1.22299
1.22140275816
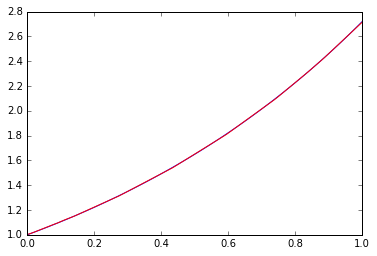
Sounds good. So how well can the function fit in the range 0 to 1?
x=np.linspace(0,1,100)
plt.plot(x,np.exp(x))
plt.hold(True)
p=model.predict(Variable(x.astype(np.float32).reshape(100,1))).data
_=plt.plot(x, p,"r")

Blue is the correct answer and red is the learning result.
feel well. This fit performance cannot be achieved with linear functions alone. It is interesting to change the depth, width (number of dimensions), etc. of the net, but as is often said, it can be confirmed that nonlinear elements and depth are more important than width.
Observation of learning result model
Now, let's see what kind of coefficient the model after learning the results is made of. For example, the weight $ W $ of the first layer l1 can be accessed as follows.
model.l1.W.data
array([[ 0.31513408],
[ 0.75111604],
[ 0.48637491],
[-1.34837043],
[ 0.0388922 ],
[-1.29884255],
[-0.49960354],
[ 0.35992688],
[ 0.25262424],
[-2.14205575],
[ 0.83558381],
[-0.61535668],
[ 2.15679836],
[-0.17658199],
[-1.36228967],
[-0.5751065 ]], dtype=float32)
You can use this to create a function that returns the same output with numpy, for example:
def leaky_relu(x):
#Once via ndarray to make an element-by-element operation
m = np.array((x<0))
x = np.array(x)
return np.matrix((x*0.2)*m + x*(~m))
def pseudo_exp(x):
x = np.matrix(x)
W1 = np.matrix(model.l1.W.data)
b1 = np.matrix(model.l1.b.data)
W2 = np.matrix(model.l2.W.data)
b2 = np.matrix(model.l2.b.data)
W3 = np.matrix(model.l3.W.data)
b3 = np.matrix(model.l3.b.data)
h1 = leaky_relu(W1*x+b1.T)
h2 = leaky_relu(W2*h1+b2.T)
y = leaky_relu(W3*h2+b3.T)
return y
print pseudo_exp(0.2)
print np.exp(0.2)
[[ 1.22299392]]
1.22140275816
x=np.linspace(0,1,100)
plt.plot(x,np.exp(x))
plt.hold(True)
p=pseudo_exp(x.T)
_=plt.plot(x, p.T,"r")
If you write down the coefficient values such as model.l1.W.data as they are, you can write the training result model completely with only numpy. It shouldn't be difficult to convert to a language such as C or Go. Well, chainer and numpy are fast enough for convenience, so I don't think you need to convert to another language just for speed, but if you just want to use a post-learning model, this kind of approach In some cases, it may be useful to convert to a format that does not depend on machine learning libraries such as chainer.
Observation and saving of progress
Now, when you try and error on Jupyter, you'll want to see what's going on. If you write as below, the progress plot will be updated. It depends on the convergence speed, but I try to update the display once every 10 times.
In addition, save is important. Save once in 100 times.
losses =[]
from IPython import display
model = MyChain()
optimizer = optimizers.Adam()
optimizer.setup(model)
plt.hold(False)
for i in range(500):
x,y = get_batch(100)
x_ = Variable(x.astype(np.float32).reshape(100,1))
t_ = Variable(y.astype(np.float32).reshape(100,1))
model.zerograds()
loss=model(x_,t_)
loss.backward()
optimizer.update()
losses.append(loss.data)
if i%10==0:
plt.plot(losses,"b")
plt.yscale('log')
display.clear_output(wait=True)
display.display(plt.gcf())
if i%100==0:
serializers.save_npz('my.model', model)
display.clear_output(wait=True)

Let's look at the output using the saved model.
serializers.load_npz('my.model',model)
model.get(0.2)
1.1877015
What is backpropagation?
Now, let's step into a little principle. What does it mean that parameters are optimized by backpropagation in the first place?
For simplicity, we will once return the network to a linear function ($ y = Wx + b $, $ W, b $ is just a linear expression called a scalar), and the optimizer back to a simple algorithm called SGD. Make only one batch.
Although it is the initial value of $ W, b $, by default of chainer, $ W $ is selected as a random number and $ b $ is selected as $ 0 $. Here, for the sake of clarity, the initial values are $ W = 0 and b = 0 $.
def get_batch(n):
x=np.random.random(n)
y= np.exp(x)
return x,y
class LinearChain(Chain):
def __init__(self):
super(LinearChain, self).__init__(
l1=L.Linear(1, 1,initialW=0.0),
)
def __call__(self,x,t):
return F.mean_squared_error(self.predict(x),t)
def predict(self,x):
return self.l1(x)
def get(self,x):
return self.predict(Variable(np.array([x]).astype(np.float32).reshape(1,1))).data[0][0]
For the linear function $ y = Wx + b $, we defined the square error of $ E = (y-t) ^ 2 $ as the error function.
The parameters $ W $ and $ b $ are updated in order to bring this square error closer to 0, and the update direction is defined by partially differentiating the error $ E $ with each parameter. In other words
\varDelta W = \frac{\partial E}{\partial W},\quad
\varDelta b = \frac{\partial E}{\partial b}
is. This value is called the derivative of the parameter. Expanding this formula
\begin{eqnarray*}
\varDelta W &=& \frac{\partial E}{\partial y} \frac{\partial y}{\partial W} &=& 2 \left(y-t \right) x \\
\varDelta b &=& \frac{\partial E}{\partial y} \frac{\partial y}{\partial b} &=& 2 \left( y-t \right) \\
\end{eqnarray*}
It will be. By transforming in this way, the derivative of the parameter can be expressed by the difference of the error, $ y-t $, and the known input $ x $. In the process of calculation, the difference in the error that is downstream returns to the difference in the parameters of the expression that is upstream, so it is called backpropagation. $ t, x $ are known, but $ y $ can only be obtained by calculating the forward propagation, that is, $ Wx + b $. So, if you perform the operation of backpropagation after forward propagation, you can get the difference between the parameters.
It looks like this in the figure.

Update $ W, b $ using $ \ varDelta W, \ varDelta b $ calculated in this way. SGD simply updates the parameters by multiplying the slope by a constant learning rate $ \ alpha $. In other words
W \leftarrow W-\alpha \varDelta W , \quad b \leftarrow b-\alpha\varDelta b
It will be updated like this. The default of chainer is $ \ alpha = 0.01 $.
Let's check this movement.
model2 = LinearChain()
optimizer2 = optimizers.SGD()
optimizer2.setup(model2)
losses=[]
trace=[]
def scalar(v):
#Return Valiable to scalar value
return v.data.ravel()[0]
for i in range(5):
x,y = get_batch(1)
x_ = Variable(x.astype(np.float32).reshape(1,1))
t_ = Variable(y.astype(np.float32).reshape(1,1))
model2.zerograds()
loss=model2(x_,t_)
loss.backward(retain_grad=True)
y = scalar(model2.predict(x_))
t=scalar(t_)
x=scalar(x_)
W=scalar(model2.l1.W)
b=scalar(model2.l1.b)
#Manually calculated delta_W,delta_b
dW_hand = 2*((y-t)*x)
db_hand = 2*((y-t))
#Delta calculated by chainer_W, delta_b
dW=model2.l1.W.grad.ravel()[0]
db=model2.l1.b.grad.ravel()[0]
print "====== step %d ======" % i
print "W,b \t\t\t\t%2.8f, %2.8f" % (W,b)
print "2(y-t)x,2(y-t)\t\t%2.8f, %2.8f" % (2*((y-t)*x), 2*((y-t)))
print "⊿W,⊿b\t\t\t\t%2.8f, %2.8f" % (dW,db) #delta issued by chainer_W, delta_b
print "W-α⊿W,b-α⊿b \t\t%2.8f, %2.8f" % (W-0.01*dW,b-0.01*db)
optimizer2.update()
====== step 0 ======
W,b 0.00000000, 0.00000000
2(y-t)x,2(y-t) -3.58069563, -4.46209097
⊿W,⊿b -3.58069563, -4.46209097
W-α⊿W,b-α⊿b 0.03580696, 0.04462091
====== step 1 ======
W,b 0.03580695, 0.04462091
2(y-t)x,2(y-t) -0.08072093, -1.99062216
⊿W,⊿b -0.08072093, -1.99062216
W-α⊿W,b-α⊿b 0.03661416, 0.06452713
====== step 2 ======
W,b 0.03661416, 0.06452713
2(y-t)x,2(y-t) -1.16285205, -2.84911036
⊿W,⊿b -1.16285205, -2.84911036
W-α⊿W,b-α⊿b 0.04824269, 0.09301824
====== step 3 ======
W,b 0.04824268, 0.09301823
2(y-t)x,2(y-t) -0.44180280, -2.23253369
⊿W,⊿b -0.44180280, -2.23253369
W-α⊿W,b-α⊿b 0.05266071, 0.11534357
====== step 4 ======
W,b 0.05266071, 0.11534357
2(y-t)x,2(y-t) -1.07976472, -2.70742726
⊿W,⊿b -1.07976472, -2.70742726
W-α⊿W,b-α⊿b 0.06345836, 0.14241784
The following two points can be confirmed.
-Chainer's grad returns the same value as the manual calculation of $ 2 (y-t) x, 2 (y-t) $ --SGD updates $ W and b $ by 0.01 grad
Looking at chainer Linear Source, it is written so that it can handle multiple inputs and outputs. It is a little difficult to understand because it is, but forward () is output as $ Wx + b $, and backward () is output as the derivative of $ W $ by multiplying the derivative grad_outputs in the latter stage by $ x $. You can see that it is described. The output of backward () returns all the derivatives of $ x, W, b $.
Also, if you look at the SGD Source, grad will have lr = 0.01 when update () is called. (lr is an abbreviation for learning rate) is multiplied and returned as a parameter.
Now, let's see how the update results in approaching the optimum value.
import matplotlib.path as mpath
import matplotlib.patches as patches
#Draw the contour lines of Ross
psize=40
W=np.linspace(-1,3,psize)
B=np.linspace(-1,3,psize)
Wm, Bm = np.meshgrid(W, B)
Z=np.zeros((psize,psize))
for w in range(psize):
for b in range(psize):
Z[b,w]=0.0
for x in np.linspace(0,1,10):
Z[b,w] += (W[w]*x+B[b]-np.exp(x))**2
plt.contourf(Wm,Bm, Z, 100,vmax=80,vmin=0)
plt.colorbar()
plt.hold(True)
model2 = LinearChain()
optimizer2 = optimizers.SGD()
optimizer2.setup(model2)
losses=[]
verts = [ ]
batchsize=20
for i in range(1000):
x,y = get_batch(batchsize)
x_ = Variable(x.astype(np.float32).reshape(batchsize,1))
t_ = Variable(y.astype(np.float32).reshape(batchsize,1))
#Save progress once every 10 times
if i%10==0:
w= model2.l1.W.data[0][0]
b = model2.l1.b.data[0]
verts.append((w,b))
model2.zerograds()
loss=model2(x_,t_)
loss.backward()
optimizer2.update(retain_grad=True)
#Plot the progress
xs, ys = zip(*verts)
_=plt.plot(xs, ys, 'o', lw=1, color='white') #, ms=10)

The horizontal axis is $ W $ and the vertical axis is $ b $. Contour lines show loss. You can see that it is heading towards the bottom.
Of course, because of the simplification, the fit result is straight even at the optimum point. It's a least squares near straight line. It is shown below.
x=np.linspace(0,1,100)
plt.plot(x,np.exp(x))
plt.hold(True)
p=model2.predict(Variable(x.astype(np.float32).reshape(100,1))).data
_=plt.plot(x, p,"r")

With the above, we learned how to use chainer by optimizing a neural network that approximates the function $ y = e ^ x $. It's just a touch, but I touched on the principle of optimization and how it proceeds.
Recommended Posts