OpenGoddard How to use 2-python library for nonlinear optimal control and orbit generation
https://github.com/istellartech/OpenGoddard https://istellartech.github.io/OpenGoddard/
How to use OpenGoddard 1 How to use OpenGoddard 2 ← Now here How to use OpenGoddard 3 How to use OpenGoddard 4
Goddard problem (optimal rocket ascent control problem in the atmosphere)
We will solve the Goddard problem, which is a classic problem in rocket engineering, and the problem of optimum thrust control for the optimum ascent of a rocket in the atmosphere. See the example file for details.
Equation of motion
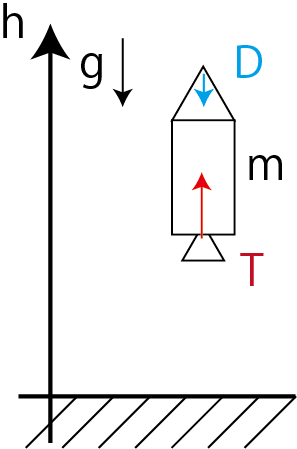
Consider the movement of a rocket in one dimension (only height). Consider the thrust and air resistance of the rocket engine to maximize the altitude. T: Thrust D: Drag (air resistance) g: Gravity acceleration
\begin{align}
\dot{h} &= v \\
\dot{v} &= \frac{T - D}{m} - g \\
\dot{m} &= - \frac{T}{c}
\end{align}
Restraint condition
Enter the upper and lower limits of the initial condition, end value condition, state variable, and control variable.
Evaluation function
Put the value you want to minimize in return. Here, we want to maximize the altitude, so pay attention to the code as follows.
J = -h
result

The result was that it was better to use full throttle at first and then reduce the thrust in the middle. This is a balance between the property that the thrust should be as large as possible in order to reduce the deceleration due to gravity in terms of phenomenon, and the property that it is better not to accelerate too much in a dense air because the air resistance should be small. The result. In jargon, it is the minimization of the sum of gravity loss and aerodynamic loss. The same thing is actually considered in the actual rocket, and in the solid fuel rocket, the thrust is adjusted to a good feeling on the way. The solution to the Goddard problem is in use! Optimization problems are useful to the world! Wow!
knotting method The pseudo-spectral method, which is the content of OpenGoddard, is a great algorithm, but I am not good at state variables and control variables that are not smooth (not differentiable). I'm not good at changing control variables discontinuously. Also, I'm not good at absolute values. In terms of the Goddard problem, it only solves the altitude, speed, weight, and thrust so that it is smooth. The knotting method is used as a method for finding solutions for state variables and control variables even if they are discontinuous at a specific point. This is a method of dividing the calculation interval by discontinuous parts. Open Goddard makes it easy to use the knotting method. (There is also algorithm optimization software that automatically divides the knotting method section in the world ...)
Goddard problem (with knot)
List the values to put in the Problem class.
time_init = [0.0, 0.1, 0.3]
n = [25, 25]
num_states = [3, 3]
num_controls = [1, 1]
It also specifies which equation of motion is applied for each interval and whether the state variables are continuous. Here, True is selected with the expectation that only the control variables will change discontinuously. The True / False here and the constraint condition are closely related, so specify them carefully. If False, it will diverge unless the variable is fixed at the knot point in the constraint condition (equality).
prob.dynamics = [dynamics, dynamics]
prob.knot_states_smooth = [True]
From the above,

With knot, the maximum altitude has dropped. .. .. It wasn't very good. It's not just a good idea to use the knotting method like this, but now you can handle problems with non-contiguous variables.
Recommended Posts