How to use OpenGoddard 3-python library for nonlinear optimal control and orbit generation
https://github.com/istellartech/OpenGoddard https://istellartech.github.io/OpenGoddard/
How to use OpenGoddard 1 How to use OpenGoddard 2 How to use OpenGoddard 3 ← Now here How to use OpenGoddard 4
Optimal rocket climb (1st stage)
As a combination of the normalization (scaling) and knotting method that we have tried so far, thrust control optimization is performed with a value close to that of an actual rocket.
As a reference problem, refer to the optimal rocket climb problem described in the following paper. The algorithm inside also uses the same Legendre-Gauss-Lobatto pseudo-spectral method as Open Goddard.
Rea, Jeremy Ryan. A legendre pseudospectral method for rapid optimization of launch vehicle trajectories. Diss. Massachusetts Institute of Technology, 2001. http://hdl.handle.net/1721.1/8608
The equation of motion is almost the same as How to use 2. Change only the value. Don't forget to normalize, as changing the value will require a number for normalization.
After that, write it in a good way SOLVE!
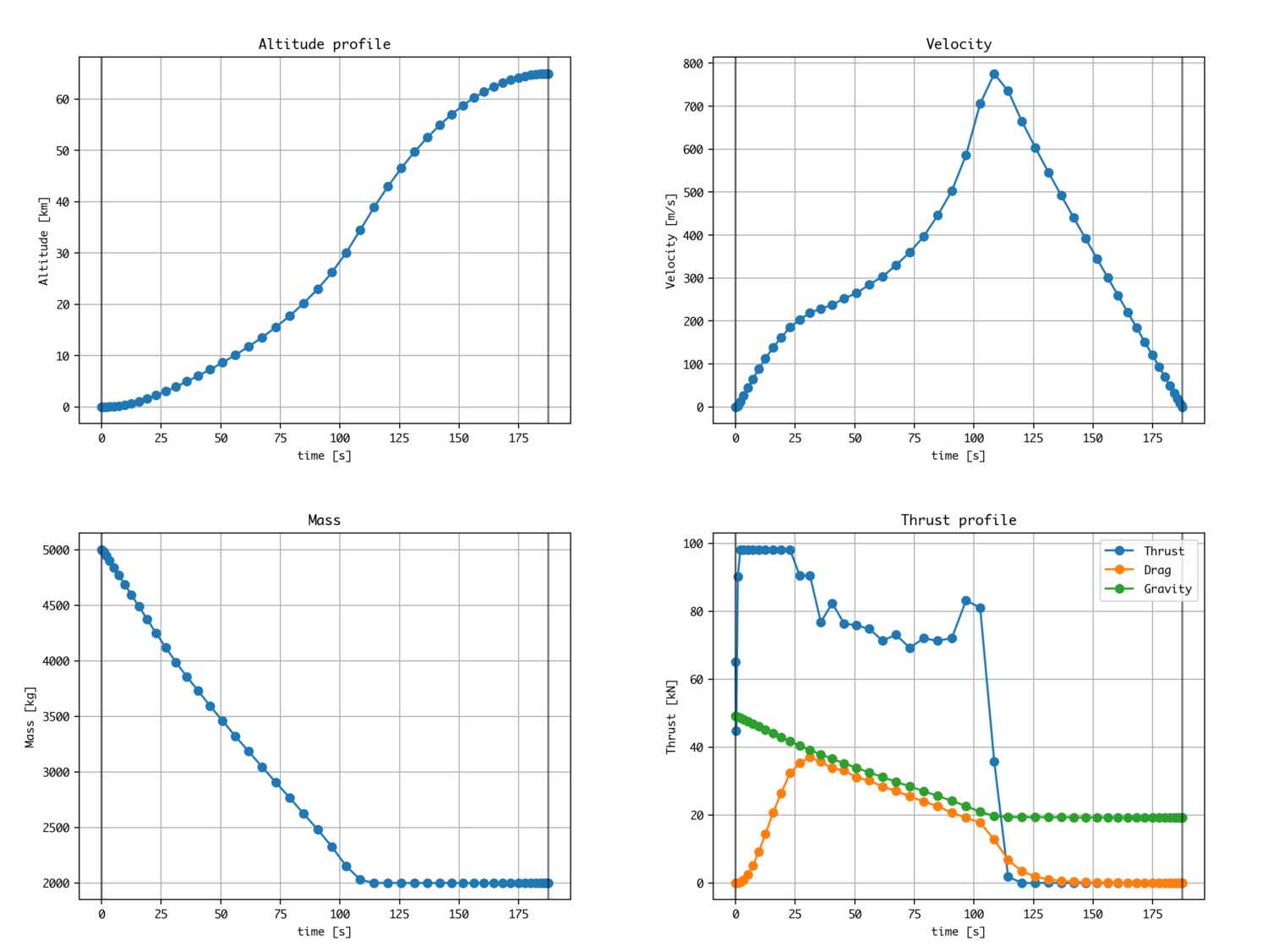
The graph is similar to the paper. (It differs slightly depending on how the convergence value is set)
Optimal rocket climb (2 steps)
The thrust control optimization of the two-stage rocket is performed using the knotting method. The main changes are as follows. The default solution (Guess part) has also been changed a little.
time_init = [0.0, 300, 600]
n = [25, 25]
num_states = [3, 3]
num_controls = [1, 1]
max_iteration = 30
prob = Problem(time_init, n, num_states, num_controls, max_iteration)
prob.dynamics = [dynamics, dynamics]
prob.knot_states_smooth = [False]
The state variable (mass here) is defined as discontinuous. Add the following to the constraints:
# knotting condition
R1 = prob.states(0, 0)
v1 = prob.states(1, 0)
m1 = prob.states(2, 0)
R2 = prob.states(0, 1)
v2 = prob.states(1, 1)
m2 = prob.states(2, 1)
result.add(R1[-1] - R2[0])
result.add(v1[-1] - v2[0])
result.add(m1[-1] - m2[0] - 1200)
If you put in, the altitude and velocity are continuous, and you can define the mass loss (discontinuous) at the time of separation.
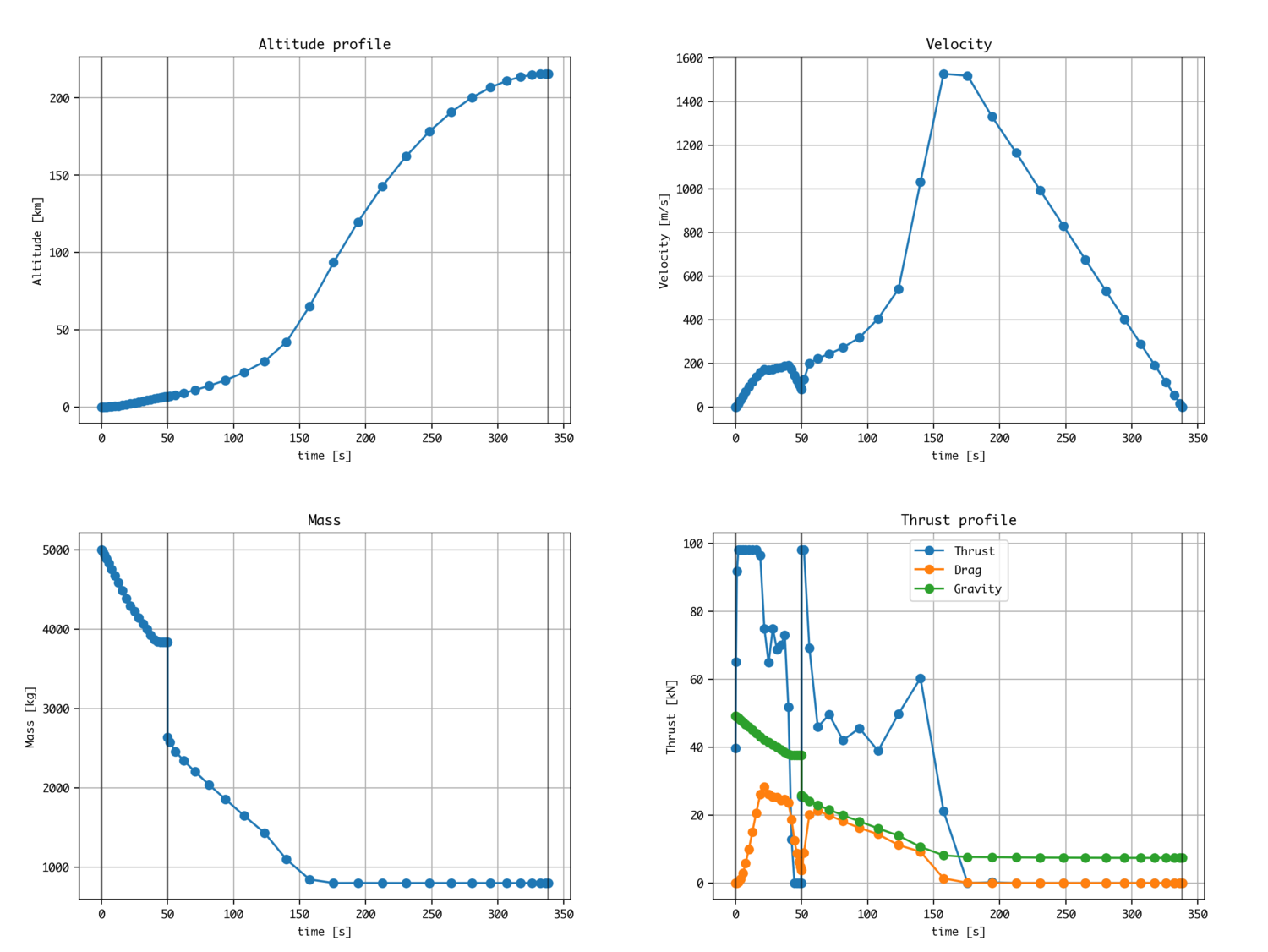
Two-stage rocket in two-dimensional coordinates
The example of OpenGoddard includes an example assuming the orbit insertion of a rocket into low earth orbit in two dimensions (polar coordinate system).


The result of Open Goddard is that it is best to stop the upper stage rocket and reignite it in order to insert it into orbit. Space engineers around the world are developing rockets, etc. based on the results of these optimal orbits.
By the way
The method that does not reignite is called the direct burn method, but the required technical level is lower for the direct burn, and in reality, the direct burn may be adopted due to communication with the ground or technical problems. In reality, it is required to create an orbit with various restraint conditions.
Recommended Posts