[Python] Dessinez des données d'altitude sur une surface sphérique avec Plotly et dessinez un globe qui peut être tourné en rond et en rond
introduction
Il prend en charge divers langages, y compris Python, et vous pouvez utiliser Plotly, qui vous permet de dessiner des diagrammes interactifs relativement facilement et d'utiliser les données d'altitude pour faire une rotation comme Google Earth. Créons un globe.
Le résultat ressemble à ceci. https://rkiuchir.github.io/3DSphericalTopo
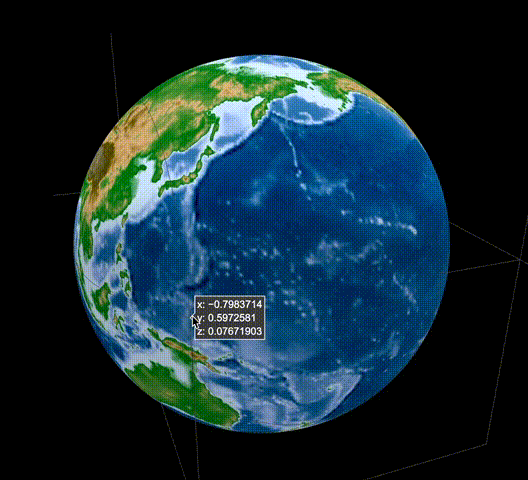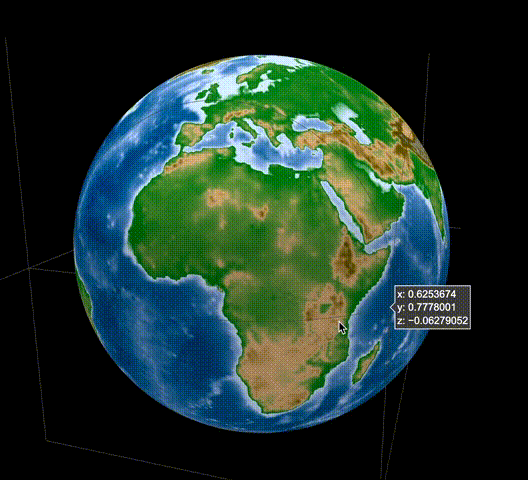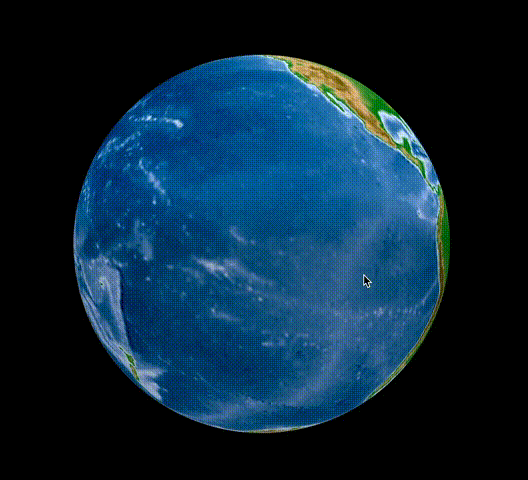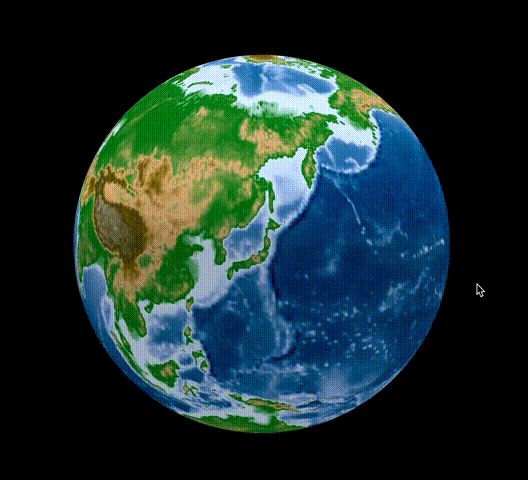
3 points
- Acquisition et lecture des données d'élévation
- Convertissez les informations de latitude et de longitude exprimées dans le système de coordonnées orthogonales en système de coordonnées sphériques ([Plotly Chart Studio: Heatmap plot on a spherical map](https://chart-studio.plotly.com/~empet/14813/heatmap] -voir un tracé sur une carte sphérique / # /))
- Dessiner avec Plotly
Environnement d'exécution
- macOS 10.14 Mojave
- Python 3.6 (Anaconda)
- Jupyter notebook
0. Installer tracé
Il peut être installé avec pip install plotly.
1-1. Acquisition des données d'altitude
- Les données d'altitude (ETOPO1 Global Relief Model) avec une résolution de 1 minute dans le monde sont disponibles dans NOAA (National Oceanic and Atmospheric Administration). Ce site](https://www.ngdc.noaa.gov/mgg/global/) est disponible.
- Cette fois, téléchargez le fichier au format netCDF enregistré sur la grille (ETOPO1_Ice_g_gdal.grd) de ETOPO1 Ice Surface.
1-2. Lecture des données d'altitude
Tout d'abord, lisez les trois données de latitude / longitude et d'altitude du fichier de données au format netCDF.
- L'entrée définie ici est la latitude (lat_area), la longitude (lon_area) et la résolution (résolution) de la zone spécifiée.
- La sortie est le type de maillage latitude (lon), longitude (lat) et résolution (topo) dans la zone spécifiée.
- La partie résolution est spécifiée au format ° (degré), et la spécification de résolution la plus élevée est 0,0167 °.
Concernant la résolution, les données sont ignorées selon la valeur de résolution spécifiée.
import numpy as np
from netCDF4 import Dataset
def Etopo(lon_area, lat_area, resolution):
### Input
# resolution: resolution of topography for both of longitude and latitude [deg]
# (Original resolution is 0.0167 deg)
# lon_area and lat_area: the region of the map which you want like [100, 130], [20, 25]
###
### Output
# Mesh type longitude, latitude, and topography data
###
# Read NetCDF data
data = Dataset("ETOPO1_Ice_g_gdal.grd", "r")
# Get data
lon_range = data.variables['x_range'][:]
lat_range = data.variables['y_range'][:]
topo_range = data.variables['z_range'][:]
spacing = data.variables['spacing'][:]
dimension = data.variables['dimension'][:]
z = data.variables['z'][:]
lon_num = dimension[0]
lat_num = dimension[1]
# Prepare array
lon_input = np.zeros(lon_num); lat_input = np.zeros(lat_num)
for i in range(lon_num):
lon_input[i] = lon_range[0] + i * spacing[0]
for i in range(lat_num):
lat_input[i] = lat_range[0] + i * spacing[1]
# Create 2D array
lon, lat = np.meshgrid(lon_input, lat_input)
# Convert 2D array from 1D array for z value
topo = np.reshape(z, (lat_num, lon_num))
# Skip the data for resolution
if ((resolution < spacing[0]) | (resolution < spacing[1])):
print('Set the highest resolution')
else:
skip = int(resolution/spacing[0])
lon = lon[::skip,::skip]
lat = lat[::skip,::skip]
topo = topo[::skip,::skip]
topo = topo[::-1]
# Select the range of map
range1 = np.where((lon>=lon_area[0]) & (lon<=lon_area[1]))
lon = lon[range1]; lat = lat[range1]; topo = topo[range1]
range2 = np.where((lat>=lat_area[0]) & (lat<=lat_area[1]))
lon = lon[range2]; lat = lat[range2]; topo = topo[range2]
# Convert 2D again
lon_num = len(np.unique(lon))
lat_num = len(np.unique(lat))
lon = np.reshape(lon, (lat_num, lon_num))
lat = np.reshape(lat, (lat_num, lon_num))
topo = np.reshape(topo, (lat_num, lon_num))
return lon, lat, topo
2. Convertissez les informations de latitude et de longitude en coordonnées sphériques
(Voir Plotly Chart Studio: tracé Heatmap sur une carte sphérique)
Ici, les informations de latitude et de longitude exprimées par les coordonnées du système orthogonal préparées ci-dessus sont converties en système de coordonnées sphériques.
def degree2radians(degree):
# convert degrees to radians
return degree*np.pi/180
def mapping_map_to_sphere(lon, lat, radius=1):
#this function maps the points of coords (lon, lat) to points onto the
sphere of radius radius
lon=np.array(lon, dtype=np.float64)
lat=np.array(lat, dtype=np.float64)
lon=degree2radians(lon)
lat=degree2radians(lat)
xs=radius*np.cos(lon)*np.cos(lat)
ys=radius*np.sin(lon)*np.cos(lat)
zs=radius*np.sin(lat)
return xs, ys, zs
3. Dessiner avec Plotly
Maintenant, dessinons en fait les données tridimensionnelles de latitude, longitude et altitude représentées par le système de coordonnées sphériques dans Plotly.
Tout d'abord, appelez la fonction préparée en 1-2. Pour lire les données d'altitude globales. Si vous le lisez avec une résolution trop élevée, la quantité de données sera importante de l'ordre du cube, donc cette fois la résolution est réglée à 0,8 °.
# Import topography data
# Select the area you want
resolution = 0.8
lon_area = [-180., 180.]
lat_area = [-90., 90.]
# Get mesh-shape topography data
lon_topo, lat_topo, topo = ReadGeo.Etopo(lon_area, lat_area, resolution)
Ensuite, convertissez-le en système de coordonnées sphériques avec la fonction préparée en 2.
xs, ys, zs = mapping_map_to_sphere(lon_topo, lat_topo)
Et à partir de là, nous passerons réellement au dessin.
Tout d'abord, définissez l'échelle de couleurs utilisée pour dessiner les données d'élévation.
# Import color scale
import Plotly_code as Pcode
name = "topo"
Ctopo = Pcode.Colorscale_Plotly(name)
cmin = -8000
cmax = 8000
Ensuite, dessinez en utilisant Plotly. Ici, vous entrez les données d'entrée et l'échelle de couleurs.
topo_sphere=dict(type='surface',
x=xs,
y=ys,
z=zs,
colorscale=Ctopo,
surfacecolor=topo,
cmin=cmin,
cmax=cmax)
)
Effacez l'arbre, etc. pour qu'il soit beau.
noaxis=dict(showbackground=False,
showgrid=False,
showline=False,
showticklabels=False,
ticks='',
title='',
zeroline=False)
Enfin, utilisez la mise en page pour spécifier le titre et la couleur d'arrière-plan. Cette fois, la couleur de fond est noire, avec un peu de conscience de Google Earth.
import plotly.graph_objs as go
titlecolor = 'white'
bgcolor = 'black'
layout = go.Layout(
autosize=False, width=1200, height=800,
title = '3D spherical topography map',
titlefont = dict(family='Courier New', color=titlecolor),
showlegend = False,
scene = dict(
xaxis = noaxis,
yaxis = noaxis,
zaxis = noaxis,
aspectmode='manual',
aspectratio=go.layout.scene.Aspectratio(
x=1, y=1, z=1)),
paper_bgcolor = bgcolor,
plot_bgcolor = bgcolor)
Ensuite, dessinez en utilisant celui préparé (ici, sortie html).
from plotly.offline import plot
plot_data=[topo_sphere]
fig = go.Figure(data=plot_data, layout=layout)
plot(fig, validate = False, filename='3DSphericalTopography.html',
auto_open=True)
en conclusion
Avec cela, je pense que je pourrais dessiner un tracé d'un globe qui peut être tourné comme au début. Je l'utilise en superposant la distribution des tremblements de terre en plus de cela.
Cet exemple peut être facilement appliqué lors du traçage sur une sphère, et je pense qu'il a un large éventail d'utilisations. De plus, il est utile non seulement pour les données d'altitude, mais aussi pour créer une carte en deux dimensions, et il est également possible de dessiner des images en trois dimensions qui expriment la hauteur avec des données d'altitude.
Recommended Posts