OpenGoddard Comment utiliser la bibliothèque 2-python pour un contrôle optimal non linéaire et la génération de trajectoires

https://github.com/istellartech/OpenGoddard https://istellartech.github.io/OpenGoddard/

Comment utiliser OpenGoddard 1 Ouvrir Goddard Comment utiliser 2 ← Maintenant ici Comment utiliser OpenGoddard 3 Ouvrir Goddard Comment utiliser 4

Problème de Goddard (problème de contrôle optimal de la remontée des fusées dans l'atmosphère)

Nous allons résoudre le problème de Goddard, qui est un problème classique dans l'ingénierie des fusées, le problème du contrôle optimal de la poussée pour l'ascension optimale d'une fusée dans l'atmosphère. Voir le fichier exemple pour plus de détails.

Équation du mouvement

Considérez le mouvement de la fusée dans une dimension (seulement la hauteur). Pensez à maximiser l'altitude en tenant compte de la poussée et de la résistance à l'air du moteur-fusée. T: poussée D: résistance (résistance à l'air) g: accélération de la gravité

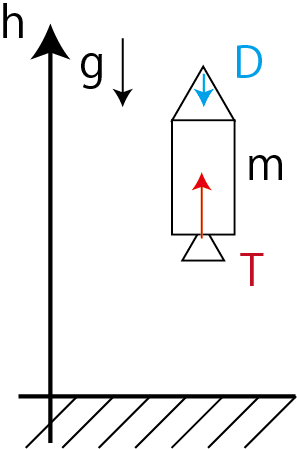
\begin{align}
\dot{h} &= v \\
\dot{v} &= \frac{T - D}{m} - g \\
\dot{m} &= - \frac{T}{c}
\end{align}

Condition de contention

Entrez les limites supérieure et inférieure de la condition initiale, de la condition de valeur finale, de la variable d'état et de la variable de contrôle.

Fonction d'évaluation

Mettez la valeur que vous souhaitez minimiser en retour. Ici, nous voulons maximiser l'altitude, alors faites attention au signe comme suit.

J = -h

résultat

Le résultat était qu'il valait mieux utiliser les pleins gaz dans un premier temps, puis réduire la poussée au milieu. Il s'agit d'un équilibre entre la propriété selon laquelle la poussée doit être aussi grande que possible afin de réduire la décélération due à la gravité en termes de phénomène, et la propriété qu'il vaut mieux ne pas trop accélérer dans un air dense car la résistance de l'air doit être faible. Le résultat. En termes techniques, c'est la minimisation de la somme de la perte de gravité et de la perte aérodynamique. La même chose est en fait considérée dans la fusée réelle, et dans la fusée à combustible solide, la poussée est ajustée à une bonne sensation en cours de route. La solution au problème de Goddard est en cours d'utilisation! Les problèmes d'optimisation sont utiles au monde! Hou la la!

knotting method La méthode pseudo-spectrale, qui est le contenu d'OpenGoddard, est un excellent algorithme, mais je ne suis pas doué pour les variables d'état et les variables de contrôle qui ne sont pas lisses (non différentiables). Je ne suis pas doué pour modifier les variables de contrôle de manière discontinue. De plus, je ne suis pas doué pour les valeurs absolues. En ce qui concerne le problème de Goddard, il ne résout que pour que l'altitude, la vitesse, le poids et la poussée soient lisses. La méthode de nouage est utilisée comme méthode pour trouver des solutions pour les variables d'état et les variables de contrôle même si elles sont discontinues en un point spécifique. Il s'agit d'une méthode de division de l'intervalle de calcul par des parties discontinues. Open Goddard facilite l'utilisation de la méthode de nouage. (Il existe également un logiciel d'optimisation d'algorithme qui divise automatiquement la section de méthode de nouage dans le monde ...)

Problème de Goddard (avec noeud)

Répertoriez les valeurs à mettre dans la classe Problème.

time_init = [0.0, 0.1, 0.3]
n = [25, 25]
num_states = [3, 3]
num_controls = [1, 1]

Il spécifie également quelle équation de mouvement est appliquée pour chaque intervalle et si les variables d'état sont continues. Ici, True est sélectionné avec l'espoir que seules les variables de contrôle changeront de manière discontinue. Le vrai / faux ici et la condition de contrainte sont étroitement liés, spécifiez-les donc soigneusement. Si False, il diverge à moins que la variable ne soit fixée au point de nœud dans la condition de contrainte (égalité).

prob.dynamics = [dynamics, dynamics]
prob.knot_states_smooth = [True]

De ce qui précède,

Avec noeud, l'altitude maximale a baissé. .. .. Ce n'était pas très bon. Ce n'est pas seulement une bonne idée d'utiliser la méthode de nouage comme celle-ci, mais vous pouvez maintenant gérer le problème des variables discontinues.