Comment utiliser la bibliothèque OpenGoddard 1-python pour un contrôle optimal non linéaire et la génération de trajectoires

Comment utiliser Open Goddard 1

OpenGoddard est une bibliothèque python pour trouver des solutions numériques à mes problèmes de contrôle optimal non linéaires.

https://github.com/istellartech/OpenGoddard https://istellartech.github.io/OpenGoddard/

Ici, un exemple d'utilisation réelle est expliqué.

Comment utiliser OpenGoddard 1 ← Maintenant ici Comment utiliser OpenGoddard 2 Comment utiliser OpenGoddard 3 Comment utiliser OpenGoddard 4

Problème d'optimisation

Les problèmes de contrôle optimal sont des problèmes d'optimisation contraints, et les problèmes d'optimisation sont [wikipedia](https://ja.wikipedia.org/wiki/%E6%9C%80%E9%81%A9%E5% Comme décrit dans 8C% 96% E5% 95% 8F% E9% A1% 8C), il existe plusieurs types selon la forme de la fonction d'évaluation et la présence ou l'absence de contraintes. OpenGoddard est une bibliothèque de résolution de problèmes de programmation non linéaire (PNL) = contrôle optimal non linéaire. Problème de contrôle optimal non linéaire = Programmation non linéaire → [Programmation secondaire séquentielle](https://ja.wikipedia.org/wiki/%E9%80%90%E6%AC%A1%E4%BA%8C%E6% AC% A1% E8% A8% 88% E7% 94% BB% E6% B3% 95) (programmation quadratique séquentielle, SPQ). Dans OpenGoddard, si vous entrez la fonction d'évaluation, l'équation de mouvement, la condition de contrainte et la condition de calcul, ajoutez la condition de contrainte de la méthode appelée méthode pseudospectrale et ajoutez la condition de contrainte dans Scipy de python. Il est résolu par le solveur de programmation secondaire séquentiel (SLSQP). L'utilisateur n'a qu'à entrer la fonction d'évaluation, l'équation cinétique (équation différentielle normale), la condition de contrainte et la condition de calcul sans regarder la méthode à l'intérieur.

Problème de descente le plus rapide

Un exemple classique d'un problème de contrôle optimal, prenant comme exemple le fameux problème de descente la plus rapide. Trouvez la courbe (orbite) qui permet à la balle (point de qualité) d'atteindre la distance la plus éloignée en présence de gravité, en supposant qu'il n'y a pas de frottement ou de résistance de l'air. Si vous recherchez sur Google, il sortira, mais cette courbe sera une courbe cycloïde. Pour des exemples simples tels que le problème typique de descente la plus rapide, la méthode indirecte (méthode de variation) est généralement utilisée. En effet, il est facile d'obtenir une solution analytique en convertissant des formules mathématiques. Cependant, avec des ressources informatiques abondantes, la méthode directe est plus réaliste pour une «utilisation pratique». Donc, je vais utiliser mon travail Open Goddard, qui est une bibliothèque de la méthode directe, en particulier la méthode pseudo-spectrale.

Comme écrit dans le README de github, écrivez le script python selon le flux suivant.

1. Description de la méthode et de la variable de la classe d'objets qui optimise l'orbite
2. Fonction de l'équation de mouvement
3. Fonction de contrainte
4. Fonction de fonction d'évaluation
5. Génération d'instance de problème
6. Génération d'une instance d'objet qui optimise la trajectoire
7. Réglage de l'unité pour la normalisation des variables d'optimisation (facultatif)
8. Estimation de la valeur initiale et installation (facultatif)
9. Spécification des fonctions et spécification des conditions de nouage
10. solve
11. Post-processus (visualisation)

En particulier, vous devez penser à l'avance à la partie où vous notez l'équation de mouvement, les conditions de contrainte et la fonction d'évaluation.

Équation du mouvement

L'équation du mouvement est la suivante. (Notez que la formule diffère selon la littérature en fonction de la façon de prendre l'angle)

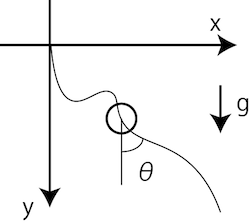
\dot{x} = v \sin{\theta} \\
\dot{y} = v \cos{\theta} \\
\dot{v} = g \cos{\theta} 

Condition de contention

Les conditions de contrainte donnent des indications telles que les conditions initiales, les conditions de terminaison et des choses qui ne sont pas physiquement étranges. Ici, la condition est que $ x = 1 $ est atteint et y peut être n'importe où.

\theta \geq 0 \\
[x(t_0), y(t_0), v(t_0), t0, x(t_f)] = [0, 0, 0, 0, 1] \\
t_f \geq 0

Fonction d'évaluation

Contient la fonction à minimiser. Ici, nous voulons trouver l'itinéraire dans le "temps le plus court", donc nous voulons minimiser le temps.

J = t_f

résultat

Pour résoudre le problème d'optimisation, il est nécessaire d'initialiser les variables d'état et les variables de contrôle. Si aucune valeur initiale n'est définie, tout sera initialisé à 0. Si vous entrez une valeur trop étrange, la solution diverge. En particulier, si vous entrez la valeur initiale qui enfreint le zéro pour cent ou la condition de contrainte, la solution ne peut pas être obtenue.

Problème de descente le plus rapide avec retenue orbitale

Pour comprendre la puissance de la méthode directe, ajoutons quelques conditions supplémentaires au problème de descente la plus rapide. Ajoutons la condition qu'il y ait une zone (mur) où la balle (point de qualité) ne doit pas entrer. Mettez ce qui suit dans la condition de contrainte.

y \leq x \tan{\theta_0} + h_0

D'autre part, il peut être résolu par la méthode des variantes, mais la solution analytique ne sortira que si la formule mathématique est falsifiée. Comme OpenGoddard, la méthode directe est une solution numérique qui n'est certainement pas optimale comme la solution analytique, mais elle est facile à trouver. Cependant, veuillez noter qu'il ne s'agit pas d'une solution optimale globale, mais d'une solution optimale locale. (Non implémenté à partir de la v1.0.0, mais il existe également une méthode qui peut confirmer l'optimum)

résultat

Vous pouvez voir que la piste est faite en observant l'état de retenue du mur. Ceci est différent de la solution analytique résolue par la méthode des variantes. Cela est dû au seuil de convergence ou au nombre insuffisant de points de division.

Le problème de la connexion de Tokyo et Osaka avec un tunnel sans friction ni résistance à l'air

En tant qu'application réelle (?) Du problème de descente la plus rapide, imaginez la distance entre Tokyo et Osaka, calculez le type de tunnel à creuser pour arriver à la vitesse la plus rapide avec une accélération de la gravité de 9,8 m / s2 et sans frottement ni résistance à l'air à une distance de 600 km. Je vais essayer.

Modifions la distance à 600 km et calculons comme elle est.

class Ball:
    def __init__(self):
        self.g = 9.8  # gravity [m/s2]
        self.l = 600000  # goal [m]
        self.h = 300000  # depth limit [m]

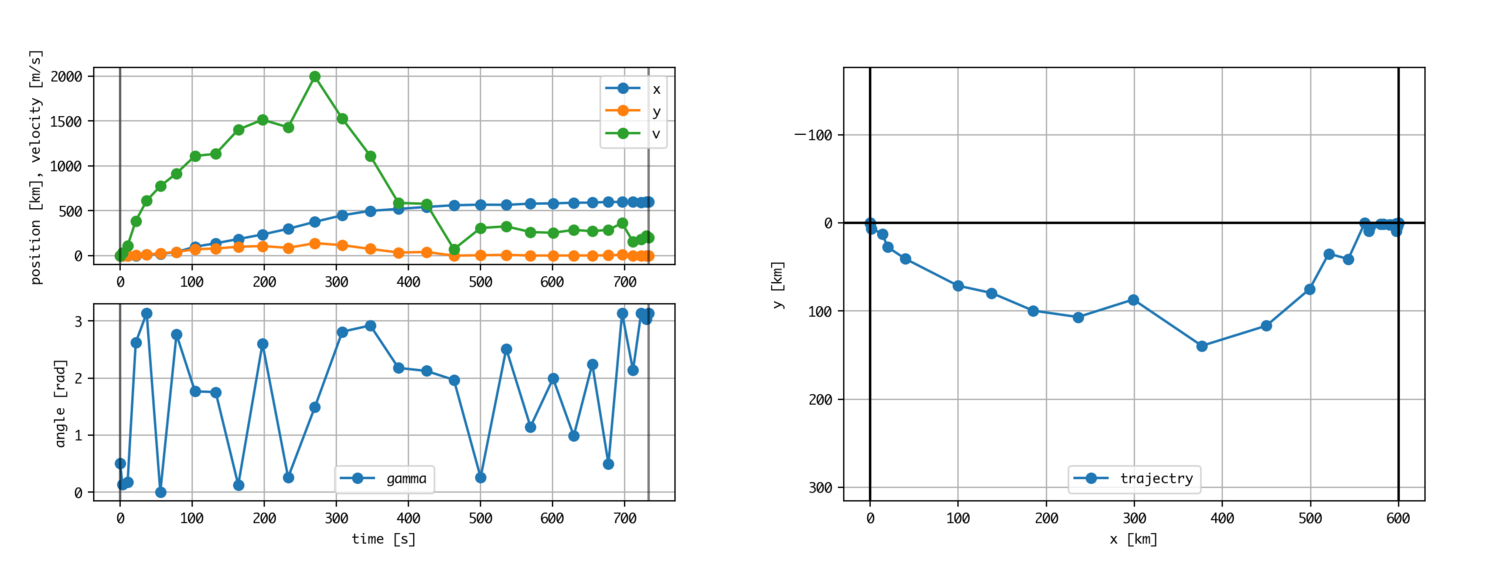
Ce n'était pas bon. La valeur de la variable de contrôle flotte et le résultat n'est pas correct. Pourquoi? Cela est dû aux variables qui sont calculées en interne.

prob.plot()

Si vous exécutez la commande ci-dessus sur ipython ou jupyter notebook après l'exécution, la méthode plot de l'instance Problem d'OpenGoddard.optimize sera appelée, et vous pourrez visualiser la valeur de la variable à l'intérieur qui est plongée dans le solveur d'optimisation.

De gauche à droite, cela signifie les variables d'état, les variables de contrôle et le temps (points). La partie la plus à gauche est la valeur de x. L'ordre des valeurs est de centaines de milliers. En revanche, v vaut plusieurs milliers et la valeur de l'angle de trajectoire θ est d'environ 0 à 3. Les solveurs de programmation quadratique séquentielle sont de mauvaise humeur si l'ordre de chaque variable n'est pas correct. La raison en est que l'ordinateur tente de minimiser la fonction d'évaluation en jouant avec les variables internes qui sont visualisées sans connaître la signification des variables, mais s'il y a des variables trop efficaces et trop inefficaces pour la fonction d'évaluation, cela ne fonctionnera pas.

Par conséquent, la normalisation est effectuée pour aligner l'ordre des variables. Définissez la variable d'état, la variable de contrôle et l'heure afin que l'ordre soit aligné. Une bonne règle de base est de garder les variables entre -10 et 10.

unit_x = 300000
unit_y = 100000
unit_t = 100
unit_v = unit_x / unit_t
prob.set_unit_states_all_section(0, unit_x)
prob.set_unit_states_all_section(1, unit_y)
prob.set_unit_states_all_section(2, unit_v)
prob.set_unit_controls_all_section(0, 1.0)
prob.set_unit_time(unit_t)

Les variables internes sont maintenant normalisées.

Cela vous donnera une solution. Arrivé en 10 minutes et 20 secondes avec une profondeur maximale de 183 km et une vitesse maximale de Mach 5,5 (1893 m / s). Dans ce tunnel, il est nécessaire de résister à une chute presque libre jusqu'à environ 100 km sous terre, et comme le trou le plus profond creusé par l'humanité semble être de 12 km, il est nécessaire de creuser plus de 10 fois cela. Eh bien, désolé, irréaliste.