Comment utiliser la bibliothèque OpenGoddard 3-python pour un contrôle optimal non linéaire et la génération de trajectoires

https://github.com/istellartech/OpenGoddard https://istellartech.github.io/OpenGoddard/

Comment utiliser OpenGoddard 1 Comment utiliser OpenGoddard 2 OpenGoddard Comment utiliser 3 ← Maintenant ici Ouvrir Goddard Comment utiliser 4

Montée optimale de la fusée (1ère étape)

En tant que technique combinée de normalisation (mise à l'échelle) et de méthode de nouage que nous avons essayée jusqu'à présent, nous effectuons une optimisation du contrôle de poussée avec une valeur proche de celle d'une fusée réelle.

Comme problème de référence, référez-vous au problème de montée de fusée optimal décrit dans l'article suivant. Cela utilise également la même méthode de pseudo-spectre Legendre-Gauss-Lobatto qu'Open Goddard.

Rea, Jeremy Ryan. A legendre pseudospectral method for rapid optimization of launch vehicle trajectories. Diss. Massachusetts Institute of Technology, 2001. http://hdl.handle.net/1721.1/8608

L'équation cinétique est presque la même que Utilisation 2. Changez uniquement la valeur. N'oubliez pas de normaliser, car la modification de la valeur nécessitera un nombre pour la normalisation.

Après cela, écrivez-le dans le bon sens SOLVE!

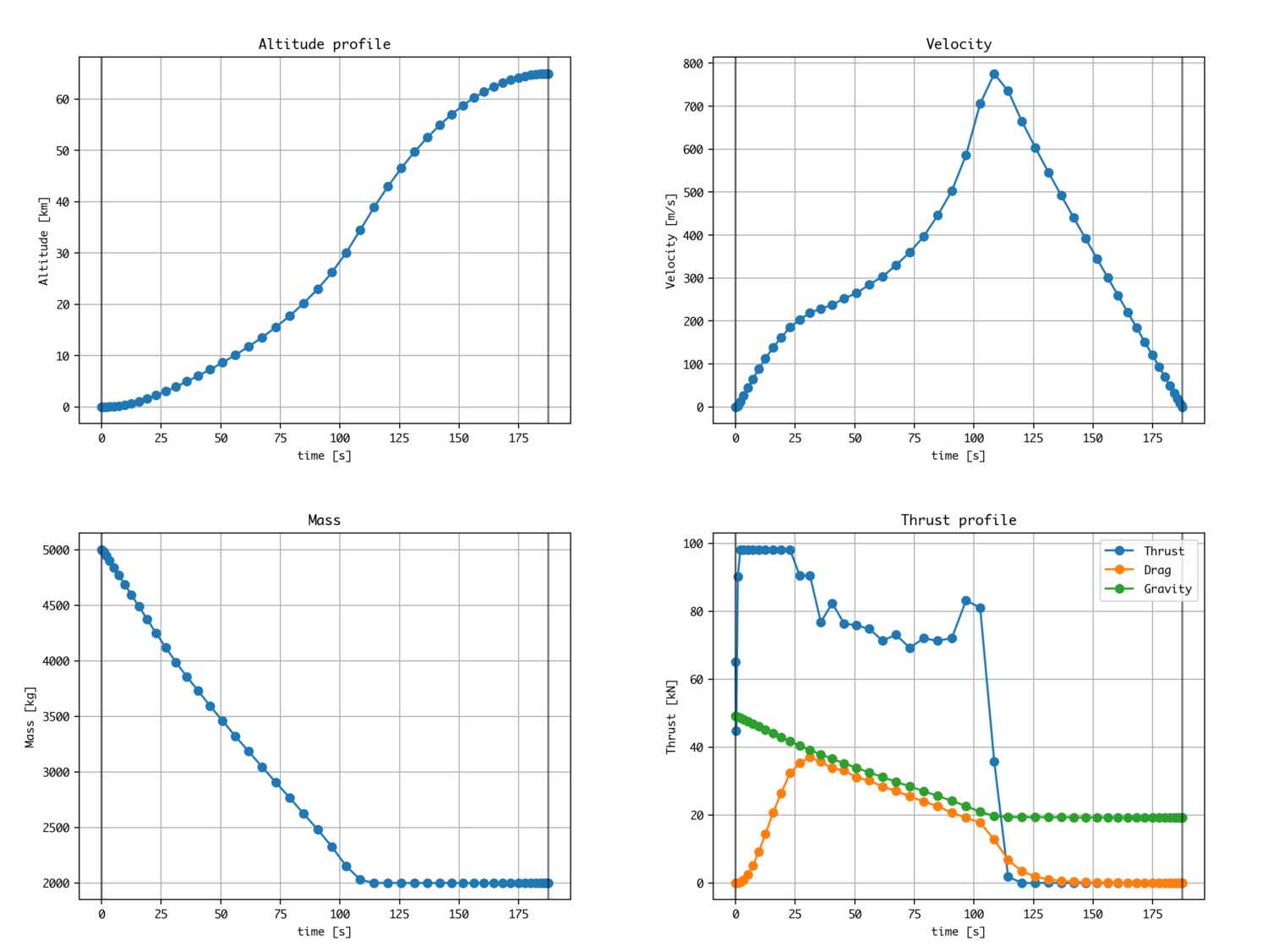
Le graphique est similaire au papier. (Il diffère légèrement selon la façon dont la valeur de convergence est définie)

Montée optimale de la fusée (2 étapes)

L'optimisation du contrôle de la poussée de la fusée à deux étages est réalisée en utilisant la méthode de nouage. Les principaux changements sont les suivants. La solution par défaut (partie Guess) a également été légèrement modifiée.

time_init = [0.0, 300, 600]
n = [25, 25]
num_states = [3, 3]
num_controls = [1, 1]
max_iteration = 30
prob = Problem(time_init, n, num_states, num_controls, max_iteration)

prob.dynamics = [dynamics, dynamics]
prob.knot_states_smooth = [False]

La variable d'état (masse ici) est définie comme discontinue. Ajoutez ce qui suit à la condition de contrainte (égalité):

# knotting condition
R1 = prob.states(0, 0)
v1 = prob.states(1, 0)
m1 = prob.states(2, 0)
R2 = prob.states(0, 1)
v2 = prob.states(1, 1)
m2 = prob.states(2, 1)
result.add(R1[-1] - R2[0])
result.add(v1[-1] - v2[0])
result.add(m1[-1] - m2[0] - 1200)

Si vous entrez, l'altitude et la vitesse sont continues et vous pouvez définir la perte de masse (discontinue) au moment de la séparation.

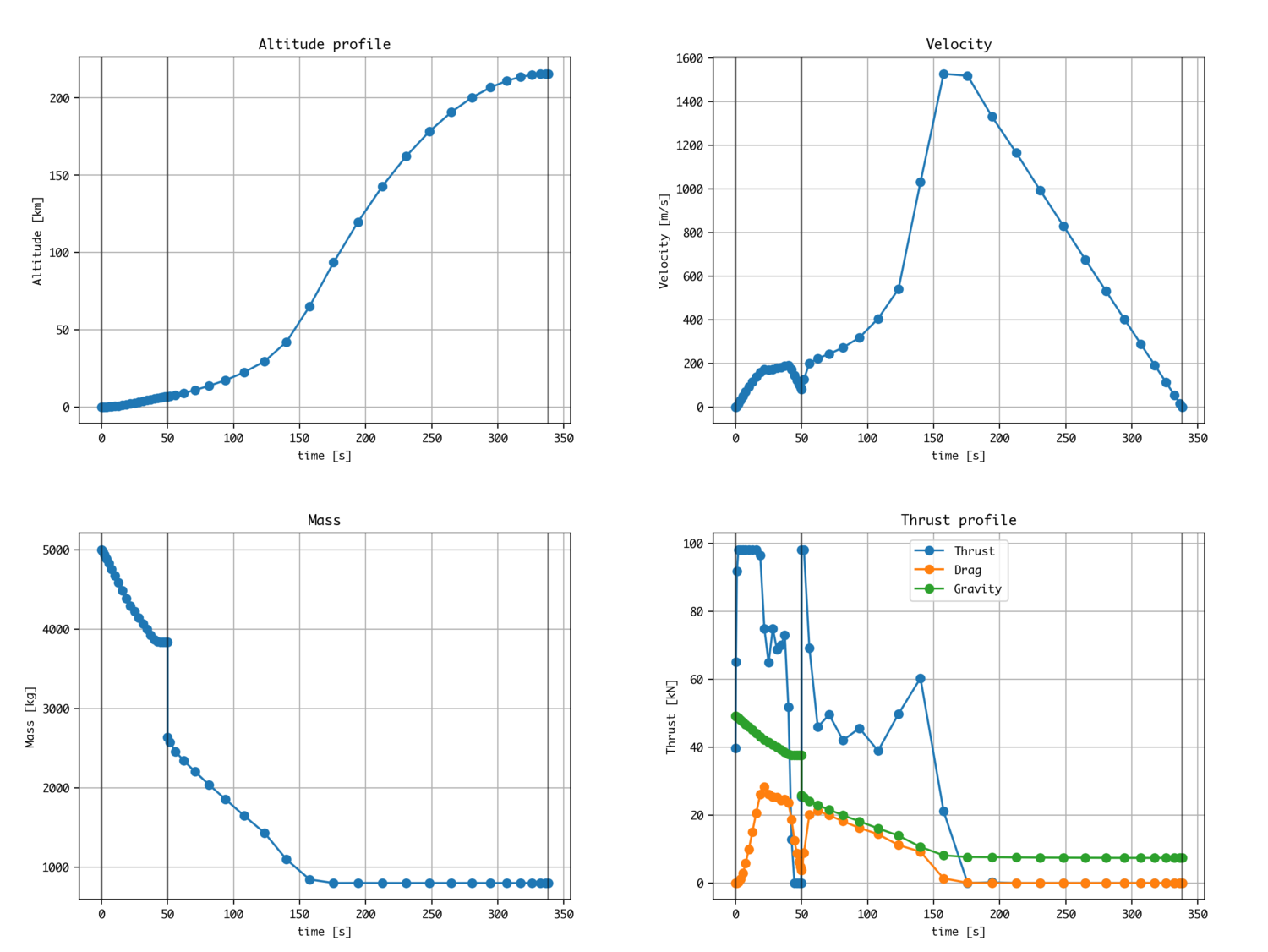
Fusée à deux étages en coordonnées bidimensionnelles

L'exemple d'OpenGoddard contient un exemple supposant que la fusée sera placée sur l'orbite terrestre basse en deux dimensions (système de coordonnées polaires).

Le résultat d'Open Goddard est qu'il est préférable d'arrêter la fusée supérieure au milieu et de la rallumer afin de la mettre en orbite. Les ingénieurs spatiaux du monde entier développent des fusées, etc. sur la base des résultats de ces orbites optimales.

Au fait

La méthode qui ne rallume pas est appelée méthode de combustion directe, mais le niveau technique requis est inférieur pour la combustion directe et, en réalité, la combustion directe peut être adoptée en raison de la communication avec le sol ou de problèmes techniques. En réalité, il est nécessaire de créer une trajectoire avec diverses conditions de contrainte.