Simulons la transition du taux d'infection par rapport à la densité de population avec python
Discramer
Je ne suis ni un expert en sciences infectieuses ou en immunologie, ni un expert en automates à cellules, donc le libellé et les numéros de prémisse sont incroyablement appropriés. Veuillez pardonner. Veuillez le voir dans le cadre du matériel sur les modèles mathématiques et la programmation python.
motivation
** On dit que le contact est réduit de 80%, mais doit-il être réduit de 70%? ** Ou ** Combien de temps faut-il pour converger? À cette époque, certaines voix disent **. Bien sûr, les chiffres exacts sont confirmés chaque jour par des tests PCR, etc., mais si vous voulez estimer grossièrement comment le nombre de personnes infectées se propage, un modèle mathématique entrera en jeu. Alors, créons un simple ** modèle de jouet ** et simulons la transition du nombre de personnes infectées dans l'ensemble de la population par rapport à une densité de population donnée, la probabilité d'infection lors d'un contact rapproché et le taux de guérison. C'était. * Puisqu'il s'agit d'un modèle de jouet, il est absurde de discuter de la politique avec cela. Cela semble persistant, mais veuillez le voir à des fins de curiosité intellectuelle. </ font>
Modèle mathématique
Pour simplifier, nous faisons les hypothèses suivantes.
-
Les résidents d'un monde plat à deux dimensions sans mer ni montagne (en bref, ** automate cellulaire **).

-
Tout le monde marche à pied et n'utilise ni le Shinkansen ni l'avion (la distance de trajet maximale pour un point temporel est de 1, et il y a aussi un mouvement diagonal).

-
Les personnes en contact étroit (cellules adjacentes) ont 20% de chances d'être infectées le lendemain.
 En d'autres termes, ** l'hypothèse selon laquelle le nombre de personnes infectées dans un cluster en contact étroit doublera en 4 jours **.
En d'autres termes, ** l'hypothèse selon laquelle le nombre de personnes infectées dans un cluster en contact étroit doublera en 4 jours **.
(1+0.20)^4 = 2.07... \approx 2
- Une personne infectée a 2% de chances d'être guérie le lendemain.
 En d'autres termes, ** l'hypothèse qu'environ la moitié des personnes infectées guérissent en un mois (31 jours) **.
En d'autres termes, ** l'hypothèse qu'environ la moitié des personnes infectées guérissent en un mois (31 jours) **.
1-(1-0.02)^{31} = 0.46... \approx 0.5
Je l'ai fait.
Le nombre de personnes infectées au temps t = 0 (jour) est de 5% du total (5 personnes sur 100 sont infectées en premier).
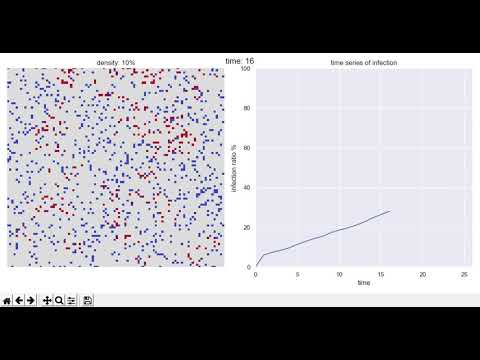
La figure de gauche montre l'état du groupe un an (365 jours) après le début, le bleu est des personnes en bonne santé </ font>, le rouge est Si vous êtes une personne infectée et qu'elle est globalement rouge vif, c'est comme une pandémie </ font>.
La figure de droite montre la transition chronologique du taux d'infection. L'axe horizontal représente le temps et l'axe vertical représente le taux d'infection. Le point est ceci ↓.

Densité de population = cas de 10% (grande ville)
C'est un cas où il y a 10 personnes dans 100 cellules. Comme vous pouvez le voir sur la figure, c'est une image d'une grande ville.
 Après un an, le groupe était dans un état de pandémie rouge vif.
En raison de la logique de la guérison naturelle, le taux d'infection n'atteint pas 100%, et il est saturé à environ 90%, mais cela n'attend pas beaucoup de convergence.
Après un an, le groupe était dans un état de pandémie rouge vif.
En raison de la logique de la guérison naturelle, le taux d'infection n'atteint pas 100%, et il est saturé à environ 90%, mais cela n'attend pas beaucoup de convergence.
Cas de densité de population = 4% (réduction de 60% des contacts)
Ne pensez-vous pas que vous vous abstenez de le faire? **En aucune façon! ** **
Ce genre de chose ne suffit pas.
 Le taux d'infection est tombé à près de 50% après un an, mais il est encore loin de converger.
Dans ce monde, les Jeux Olympiques ne peuvent avoir lieu même s'ils sont reportés d'un an.
Le taux d'infection est tombé à près de 50% après un an, mais il est encore loin de converger.
Dans ce monde, les Jeux Olympiques ne peuvent avoir lieu même s'ils sont reportés d'un an.
Cas de densité de population = 3% (réduction de 70% des contacts)
Est-il nécessaire d'avoir 70% au lieu de 80%?
** Oui, 70% n'est pas bon. ** **
 Le taux d'infection est certes assez faible, mais il augmente depuis près d'un an, quoique lentement (avec un léger pic vers la fin).
Bien que la vitesse d'infection ait été supprimée, il semble qu'un an ne soit pas suffisant pour atteindre une convergence naturelle.
Le taux d'infection est certes assez faible, mais il augmente depuis près d'un an, quoique lentement (avec un léger pic vers la fin).
Bien que la vitesse d'infection ait été supprimée, il semble qu'un an ne soit pas suffisant pour atteindre une convergence naturelle.
Cas de densité de population = 2% (réduction de 80% des contacts)
** Le nombre de nouvelles infections et le nombre de guérisseurs sont presque équilibrés. ** **
 Bien que le nouveau taux d'infection et le taux de guérison aient été décidés de manière appropriée, le résultat était assez beau.
Je suis un amateur complet, mais le nombre de réduction de 80% des contacts est-il une sorte de règle empirique en sciences infectieuses?
Bien que le nouveau taux d'infection et le taux de guérison aient été décidés de manière appropriée, le résultat était assez beau.
Je suis un amateur complet, mais le nombre de réduction de 80% des contacts est-il une sorte de règle empirique en sciences infectieuses?
Cas de densité de population = 1% (90% de réduction des contacts)
** Le nombre de personnes infectées est devenu 0 en un peu plus de 200 jours. ** **
 J'espère que le monde réel sera bientôt comme ça ~
J'espère que le monde réel sera bientôt comme ça ~
code python
Il s'agit d'une spécification qui dessine une animation qui change en temps réel. Lorsque la valeur de la cellule est 0, il n'y a personne, -1 indique une personne en bonne santé et +1 indique une personne infectée.
import numpy as np
from numpy import random
import seaborn as sns
import matplotlib.pyplot as plt
sns.set()
# parameter
density = 0.03
prob_infect = 0.20
prob_heal = 0.02
infected_initial = 0.05
# initialize earth
earth = np.where((random.random(10000) > (1 - density)), -1, 0).reshape(100, 100)
for i in range(int(10000 * density * infected_initial)):
earth[random.randint(0, 100), random.randint(0, 100)] = 1
time = 0
infection_ratio = np.zeros(10 ** 6) * np.nan
infection_ratio[time] = 0
plt.close()
fig, ax = plt.subplots(figsize=(12, 6), nrows=1, ncols=2)
no_end = True
while no_end:
for (x, y) in [(x, y) for x in range(100) for y in range(100)]:
if earth[x, y] != 0:
# infection
(x_min, x_max) = (max(x - 1, 0), min(x + 1, 98) + 1)
(y_min, y_max) = (max(y - 1, 0), min(y + 1, 98) + 1)
if np.any(earth[x_min: x_max, y_min: y_max] == 1):
earth[x, y] = 1 if random.rand() < prob_infect else earth[x, y]
# healing
earth[x, y] = -1 if random.rand() < prob_heal else earth[x, y]
# random walk around
x_next = min(max(x + random.randint(-1, 2), 0), 99)
y_next = min(max(y + random.randint(-1, 2), 0), 99)
if ((x_next, y_next) != (x, y)) & (earth[x_next, y_next] == 0):
earth[x_next, y_next] = earth[x, y]
earth[x, y] = 0
time += 1
infection_ratio[time] = np.sum(np.where(earth == 1, 1, 0)) / (10000 * density) * 100
try:
subplot0.cla()
subplot1.cla()
except:
print('no need to refresh figure')
plt.suptitle('time: {}'.format(time))
subplot0 = sns.heatmap(earth, vmin=-1, vmax=1, center=0, cmap='coolwarm', ax=ax[0], cbar=False)
ax[0].axis('off')
ax[0].set_title('density: {}%'.format(int(density * 100)))
subplot1 = sns.lineplot(data=infection_ratio)
ax[1].set_title('time series of infection')
ax[1].set_xlabel('time')
ax[1].set_ylabel('infection ratio %')
ax[1].set_ylim([0, 100])
ax[1].set_xlim([0, time + 10])
plt.tight_layout()
plt.draw()
plt.pause(0.01)
Recommended Posts