Essayez d'utiliser TensorFlow-Part 2-Convolution Neural Network (MNIST)

Cette fois, nous classerons les nombres par un réseau de neurones convolutifs utilisant MNIST.

MNIST MNIST est un ensemble de données d'images de texte manuscrit de 0 à 9. Cet ensemble de données contient 60 000 données d'entraînement avec une taille d'image de 28 x 28. Il contient 10 000 données de test. En outre, le même nombre de données d'étiquette correctes est inclus.

Utilisez cet ensemble de données pour découvrir quels sont les nombres dans l'image cible.

Préparation préalable

Téléchargez l 'exemple de code MNIST à l'avance.

Code d'implémentation complet

Le contenu de l'implémentation est basé sur [exemple de code MNIST] de TensorFlow (https://github.com/tensorflow/tensorflow/tree/master/tensorflow/examples/tutorials/mnist). Le contenu de Deep MNIST for Experts a été importé et partiellement modifié.

Le code d'implémentation complet est le suivant. Placez ce code source directement sous le répertoire mnist de l'exemple que vous avez téléchargé précédemment. ※ tensorflow/tensorflow/examples/tutorials/mnist

deep_mnist_softmax.py

from __future__ import absolute_import
from __future__ import division
from __future__ import print_function

import argparse
import sys

from tensorflow.examples.tutorials.mnist import input_data

import tensorflow as tf

#Variable de poids
def weight_variable(shape):
  initial = tf.truncated_normal(shape, stddev=0.1)
  return tf.Variable(initial)

#Variable de biais
def bias_variable(shape):
  initial = tf.constant(0.1, shape=shape)
  return tf.Variable(initial)

#Plier
def conv2d(x, W):
  return tf.nn.conv2d(x, W, strides=[1, 1, 1, 1], padding='SAME')

#mise en commun
def max_pool_2x2(x):
  return tf.nn.max_pool(x, ksize=[1, 2, 2, 1],
                        strides=[1, 2, 2, 1], padding='SAME')

def main(_):
  #L'acquisition des données
  mnist = input_data.read_data_sets('MNIST_data', one_hot=True)

  #création d'espace réservé
  x = tf.placeholder(tf.float32, [None, 784])
  y_ = tf.placeholder(tf.float32, [None, 10])

  #1ère couche de pliage
  W_conv1 = weight_variable([5, 5, 1, 32])
  b_conv1 = bias_variable([32])
  x_image = tf.reshape(x, [-1,28,28,1])
  h_conv1 = tf.nn.relu(conv2d(x_image, W_conv1) + b_conv1)
  h_pool1 = max_pool_2x2(h_conv1)

  #2ème couche de pliage
  W_conv2 = weight_variable([5, 5, 32, 64])
  b_conv2 = bias_variable([64])
  h_conv2 = tf.nn.relu(conv2d(h_pool1, W_conv2) + b_conv2)
  h_pool2 = max_pool_2x2(h_conv2)

  #Couche entièrement connectée
  W_fc1 = weight_variable([7 * 7 * 64, 1024])
  b_fc1 = bias_variable([1024])
  h_pool2_flat = tf.reshape(h_pool2, [-1, 7 * 7 * 64])
  h_fc1 = tf.nn.relu(tf.matmul(h_pool2_flat, W_fc1) + b_fc1)

  #Couche d'abandon
  keep_prob = tf.placeholder(tf.float32)
  h_fc1_drop = tf.nn.dropout(h_fc1, keep_prob)

  #Couche de sortie
  W_fc2 = weight_variable([1024, 10])
  b_fc2 = bias_variable([10])
  y_conv = tf.matmul(h_fc1_drop, W_fc2) + b_fc2

  #Fonction de perte (erreur d'entropie croisée)
  cross_entropy = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(y_conv, y_))

  #Pente
  train_step = tf.train.AdamOptimizer(1e-4).minimize(cross_entropy)

  #précision
  correct_prediction = tf.equal(tf.argmax(y_conv, 1), tf.argmax(y_, 1))
  accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))

  #session
  sess = tf.InteractiveSession()
  sess.run(tf.global_variables_initializer())

  #entraînement
  for i in range(5000):
    batch = mnist.train.next_batch(50)

    if i % 500 == 0:
      #Progression (tous les 500 cas)
      train_accuracy = accuracy.eval(feed_dict={x: batch[0], y_: batch[1], keep_prob: 1.0})
      print("step %d, training accuracy %f" % (i, train_accuracy))

    #Exécution de la formation
    train_step.run(feed_dict={x: batch[0], y_: batch[1], keep_prob: 0.5})

  #Évaluation
  print("test accuracy %f" % accuracy.eval(feed_dict={
    x: mnist.test.images, y_: mnist.test.labels, keep_prob: 1.0}))

if __name__ == '__main__':
  parser = argparse.ArgumentParser()
  parser.add_argument('--data_dir', type=str, default='/tmp/tensorflow/mnist/input_data',
                      help='Directory for storing input data')
  FLAGS, unparsed = parser.parse_known_args()
  tf.app.run(main=main, argv=[sys.argv[0]] + unparsed)

réseau neuronal

Le flux de traitement du code ci-dessus et la forme du réseau neuronal sont les suivants.

Flux de processus

forme

Détails du code d'implémentation

Les détails du code d'implémentation sont décrits ci-dessous.

• poids

#Variable de poids
def weight_variable(shape):
  initial = tf.truncated_normal(shape, stddev=0.1)
  return tf.Variable(initial)

Initialisez avec une valeur aléatoire d'une distribution normale comme variable de pondération.

--Bias

#Variable de biais
def bias_variable(shape):
  initial = tf.constant(0.1, shape=shape)
  return tf.Variable(initial)

Initialisez avec une constante (0,1) comme variable de biais.

forme [2, 3] [[0.1, 0.1, 0.1], [0.1, 0.1, 0.1]]

--Pliant

#Plier
def conv2d(x, W):
  return tf.nn.conv2d(x, W, strides=[1, 1, 1, 1], padding='SAME')

Poids (taille du filtre) Spécifiez la foulée foulées '' et le rembourrage rembourrage '' en forme de `` W '' Pliez-le.

--Mise en commun

#mise en commun
def max_pool_2x2(x):
  return tf.nn.max_pool(x, ksize=[1, 2, 2, 1],
                        strides=[1, 2, 2, 1], padding='SAME')

Spécifiez la foulée` foulées``` et le rembourrage``` padding``` sous la forme de la taille de regroupement ksize``` Effectuez la mise en commun.

ksize: comment spécifier la taille du pool Pour 2x2 [1, 2, 2, 1] Pour 3x3 [1, 3, 3, 1]

--L'acquisition des données

  #L'acquisition des données
  mnist = input_data.read_data_sets('MNIST_data', one_hot=True)

Acquiert les données MNIST.

• placeholder

 #création d'espace réservé
 x = tf.placeholder(tf.float32, [None, 784])
 y_ = tf.placeholder(tf.float32, [None, 10])

Données d'entrée: créez n x 784 comme espace réservé comme x ''. Étiqueter les données (correctes): créez n x 10 comme espace réservé comme y_ ''. L'espace réservé remplit les données au moment de l'exécution.

784 est la valeur lorsque l'image 28x28 (= 784) est traitée comme une dimension.

• Couche pliante

#1ère couche de pliage
W_conv1 = weight_variable([5, 5, 1, 32])
b_conv1 = bias_variable([32])
x_image = tf.reshape(x, [-1,28,28,1])
h_conv1 = tf.nn.relu(conv2d(x_image, W_conv1) + b_conv1)
h_pool1 = max_pool_2x2(h_conv1)

#2ème couche de pliage
W_conv2 = weight_variable([5, 5, 32, 64])
b_conv2 = bias_variable([64])
h_conv2 = tf.nn.relu(conv2d(h_pool1, W_conv2) + b_conv2)
h_pool2 = max_pool_2x2(h_conv2)

Ici, le processus est effectué selon le flux suivant.

1. Repliez avec la taille du filtre (5x5) et 32 sorties
2. Ajout de biais
3. Adapter la fonction d'activation ReLU
4. Mise en commun en taille de mise en commun (2x2)
5. Vers la deuxième couche
6. Pliez la taille du filtre (5x5), sortie 64
7. Effectuez le même traitement que la première couche à la couche entièrement connectée

--Couche de liaison complète

#Couche entièrement connectée
W_fc1 = weight_variable([7 * 7 * 64, 1024])
b_fc1 = bias_variable([1024])
h_pool2_flat = tf.reshape(h_pool2, [-1, 7 * 7 * 64])
h_fc1 = tf.nn.relu(tf.matmul(h_pool2_flat, W_fc1) + b_fc1)

[7 * 7 * 64, 1024]Est7 * 7Cependant, la taille qui a été mise en commun dans la deuxième couche de pliage, 64Cependant, le nombre de sorties dans la deuxième couche de pliage,1024Est le nombre de sorties de la couche entièrement connectée.

Ici, le processus est effectué selon le flux suivant.

1. Formatez le résultat de sortie de la deuxième couche de convolution en deux dimensions pour la multiplication
2. Multipliez par la sortie de deuxième couche convolutive (n, 7x7x64) et le poids (7x7x64, 1024)
3. Ajout de biais
4. Adapter la fonction d'activation ReLU
5. Vers la couche suivante

• Couche de chute

#Couche d'abandon
keep_prob = tf.placeholder(tf.float32)
h_fc1_drop = tf.nn.dropout(h_fc1, keep_prob)

keep_probSpécifie le taux d'abandon.

• Comme il s'agit d'un espace réservé, entrez le taux d'abandon au moment de l'exécution.

--Couche de sortie

#Couche de sortie
W_fc2 = weight_variable([1024, 10])
b_fc2 = bias_variable([10])
y_conv = tf.matmul(h_fc1_drop, W_fc2) + b_fc2

Spécifiez le nombre de classifications à afficher, `` 10 ''.

• Fonction de perte / gradient / précision

#Fonction de perte (erreur d'entropie croisée)
cross_entropy = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(y_conv, y_))

#Pente
train_step = tf.train.AdamOptimizer(1e-4).minimize(cross_entropy)

#précision
correct_prediction = tf.equal(tf.argmax(y_conv, 1), tf.argmax(y_, 1))
accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))

Spécifiez l'erreur d'entropie croisée comme fonction de perte Spécifiez Adam pour le dégradé. `` 1e-4 '' est le taux d'apprentissage. La précision est la moyenne des bonnes réponses (nombre de bonnes réponses / n).

--Session

#session
sess = tf.InteractiveSession()
sess.run(tf.global_variables_initializer())

Créez une session. ici,

sess.run(tf.global_variables_initializer())Chez tf.Initialisation de la variable.

 - entraînement

```python
#entraînement
for i in range(5000):
  batch = mnist.train.next_batch(50)

  if i % 500 == 0:
    #Progression (tous les 500 cas)
    train_accuracy = accuracy.eval(feed_dict={x: batch[0], y_: batch[1], keep_prob: 1.0})
    print("step %d, training accuracy %f" % (i, train_accuracy))

  #Exécution de la formation
  train_step.run(feed_dict={x: batch[0], y_: batch[1], keep_prob: 0.5})

Définissez le nombre de formations sur 5000 (spécifiez moins car cela prend du temps) Dans un entraînement, lisez 50 données d'entraînement à la fois et exécutez `` train_step ''. De plus, au fur et à mesure, la précision est imprimée toutes les 500 fois. (Pour la sortie de précision de cette progression, les données d'entraînement sont utilisées telles quelles en tant que données de calcul. De plus, le nombre de données est aussi petit que 50, donc la fiabilité est faible.)

Supplément ・ Mnist.train.next_batch () '' `` mélange les données quand elles sont lues jusqu'à la fin. Relisez les données depuis le début. -Feed_dict = {x: batch [0], y_: batch [1]est en train de saisir des données d'espace réservé. - Keep_prob: 0.5 spécifie un taux de chute de 50%. Si 1.0 est spécifié, il ne baissera pas. Spécifiez 1.0 pour l'évaluation et la prédiction.

--Évaluation

#Évaluation
print("test accuracy %f" % accuracy.eval(feed_dict={
  x: mnist.test.images, y_: mnist.test.labels, keep_prob: 1.0}))

Ici, la précision est calculée en utilisant 10 000 données de test.

keep_prob est 1.0 est spécifié.

## Courir

 Exécutez le code.

python deep_mnist_softmax.py

 * Lors de l'exécution dans l'environnement créé dans la précédente [Entrée](http://qiita.com/fujin/items/93aa9144d756eb85004d), exécutez après le démarrage de l'environnement virtuel.

## résultat

 Le résultat de l'exécution est le suivant.
 La précision a augmenté à 98,57%.
 Augmenter le nombre de formations devrait améliorer un peu plus la précision.

 ![sc_2017-02-001.png](https://qiita-image-store.s3.amazonaws.com/0/134550/55eafe53-65bd-e8bd-b73c-1e66b96f2ee0.png)

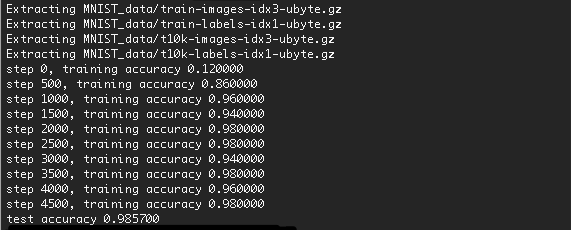
 > Cela prendra un certain temps pour la première fois car les données seront téléchargées.

 Comme mentionné ci-dessus, cette fois, nous avons effectué une classification numérique par réseau de neurones convolutifs en utilisant MNIST.