Essayez de créer un réseau de neurones en Python sans utiliser de bibliothèque
Code ici: tout le code est également disponible dans le bloc-notes Ipython sur Github.
Dans cet article, nous allons construire un simple réseau neuronal de 1 à 3 couches. Je n'expliquerai pas toutes les mathématiques qui en ressortent, mais j'aimerais expliquer les parties nécessaires d'une manière facile à comprendre. Si vous êtes intéressé par les détails des mathématiques, la plupart sont en anglais, mais voici quelques liens utiles.
- On suppose que les lecteurs de cet article connaissent au moins les bases de la différenciation et de l'apprentissage automatique (classification, régularisation, etc.). C'est encore mieux si vous connaissez des techniques d'optimisation comme la descente de dégradé. Cependant, même si vous ne connaissez pas ce qui précède, je pense que quiconque s'intéresse aux réseaux de neurones peut en profiter.
Alors pourquoi avons-nous besoin de créer un réseau neuronal à partir de zéro sans utiliser de bibliothèque? Je prévois d'utiliser des bibliothèques de réseaux neuronaux comme PyBrain et Tensorflow dans un article ultérieur, pour la raison. L'expérience de la création d'un réseau neuronal à partir de zéro, même une seule fois, est extrêmement précieuse. Concevons un modèle en sachant comment fonctionne et se construit le réseau de neurones! C'est utile dans de tels moments.
Une mise en garde est que cet article se concentre sur la lisibilité, de sorte que le code ci-dessous n'est pas écrit efficacement. J'expliquerai comment écrire du code efficace dans un prochain article. Dans ce cas, utilisez Theano.
Générer des données
Maintenant, générons d'abord les données. Heureusement, Scikit-learn a un kit de génération de jeux de données utilisable, vous n'avez donc pas à écrire votre propre code. Cette fois, créons des données en forme de lune en utilisant la fonction make_moons.
#Générer et tracer des données
np.random.seed(0)
X, y = sklearn.datasets.make_moons(200, noise=0.20)
plt.scatter(X[:,0], X[:,1], s=40, c=y, cmap=plt.cm.Spectral)

Il existe deux classes de données générées (points rouges et bleus sur le graphique). Par exemple, considérez les points bleus comme des points masculins et rouges comme des échantillons de données de patientes, et les axes X et Y comme des mesures spécifiques.
Notre objectif est de former le modèle de classification pour prédire et donner la classe correcte pour chaque point d'échantillonnage. Il est à noter que ces données ne peuvent pas être classées par ligne droite. Par conséquent, les classificateurs linéaires tels que la régression logistique ne peuvent pas constituer un bon modèle à moins que vous ne créiez vos propres entités non linéaires telles que des polynômes. Cependant, pour ces données, il est possible de créer un bon modèle en dirigeant les caractéristiques polynomiales.
Vous pouvez résoudre ce problème en dirigeant un réseau de neurones. Parce que vous n'avez pas à faire d'ingénierie de fonctionnalités. La couche cachée du réseau neuronal trouve les caractéristiques.
Retour logistique
Avant d'expliquer le réseau de neurones, commençons par former le modèle de régression logistique. Les données d'entrée sont un point sur l'axe X / Y et les données de sortie sont sa classe (0 ou 1). Voici une préparation pour l'explication du réseau de neurones ci-dessous, alors construisons un modèle de régression logistique en utilisant schikit-learn.
#Former un modèle de régression logistique
clf = sklearn.linear_model.LogisticRegressionCV()
clf.fit(X, y)
#Tracer la limite de décision
plot_decision_boundary(lambda x: clf.predict(x))
plt.title("Logistic Regression")

Dans le graphique ci-dessus, le modèle de régression logistique est entraîné et les classes sont classées avec la limite de décision comme limite. Cette bordure mène une ligne droite et la classe le plus possible, mais elle ne reconnaît pas le «mois» des données.
Former un réseau de neurones
Construisons maintenant un réseau neuronal à trois couches (1 couche d'entrée, 1 couche cachée, 1 couche de sortie). Le nombre de nœuds dans la couche d'entrée (cercles dans la figure ci-dessous) est le nombre de dimensions des données (2 cette fois). Et le nombre de nœuds dans la couche de sortie est le nombre de classes, cette fois également 2 (Au fait, comme il s'agit de 2 classes, il est possible de faire de 1 ou 0 un nœud de sortie, mais plus tard plusieurs classes Cette fois, nous utiliserons deux nœuds en considération de la manipulation). L'entrée du réseau est le point (X, Y) et la sortie est la probabilité d'être de classe 0 (femelle) ou de classe 1 (mâle). Veuillez vous référer à la figure ci-dessous.

Ensuite, déterminez les dimensions de la couche masquée (le nombre de nœuds). À mesure que le nombre de nœuds de couche masqués augmente, des modèles plus complexes peuvent être créés. D'autre part, à mesure que le nombre de nœuds augmente, la puissance de calcul est nécessaire pour apprendre et prédire les paramètres. Il est également important de noter que le risque de surajustement augmente à mesure que le nombre de paramètres augmente.
Comment choisissez-vous le nombre de couches cachées? Bien qu'il existe des lignes directrices générales, les choix se font au cas par cas et devraient être considérés plus comme de l'art que de la science. Ci-dessous, nous allons expérimenter avec quelques nombres différents de nœuds de couche masqués pour voir comment ils affectent la sortie.
Une autre chose à décider est la fonction d'activation de la couche cachée. Il s'agit d'une fonction pour transformer les données d'entrée et les sortir. Vous pouvez entraîner des données non linéaires en dirigeant une fonction d'activation non linéaire. Des exemples courants de fonctions d'activation sont Tanh, Sigmaid Function Sigmoid_function) et ReLUs. Cette fois, j'utiliserai tanh, qui peut produire des résultats relativement bons dans divers cas. Une propriété pratique de cette fonction est que vous pouvez diriger la valeur d'origine et calculer la valeur différenciée. Par exemple, la valeur différentielle de $ tanhx $ est $ 1-tanh ^ 2x $. Par conséquent, une fois que $ tanhx $ est calculé, il peut être réutilisé plus tard.
Cette fois, je veux donner une probabilité à la sortie, donc j'utiliserai la fonction Softmax pour la fonction d'activation de la couche de sortie. Vous pouvez convertir des nombres non probables en probabilités en exécutant cette fonction. Si vous êtes familier avec le modèle de régression logistique, pensez à la fonction Softmax comme une version généralisée de plusieurs classes.
Comment fonctionne la prédiction de réseau neuronal
Ce réseau de neurones utilise une sorte de multiplication matricielle appelée propagation directe et une application de la fonction d'activation définie ci-dessus. Si l'entrée x est bidimensionnelle, la valeur prédite $ \ hat {y} $ (également bidimensionnelle) est calculée comme suit.
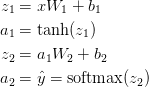
$ z_i $ est la couche d'entrée i et $ a_i $ est la couche de sortie i convertie par la fonction d'activation. $ W_1 $, $ b_1 $, $ W_2 $, $ b_2 $ sont des paramètres réseau qui doivent être appris à partir des données d'entraînement. Vous pouvez le considérer comme une transformation matricielle entre les couches réseau. Si vous regardez la multiplication de la matrice ci-dessus, vous pouvez voir le nombre de dimensions de la matrice. Par exemple, si vous utilisez 500 calques masqués, $ W_1 \ in \ mathbb {R} ^ {2 \ times 500} $, $ b_1 \ in \ mathbb {R} ^ {500} $, $ W_2 \ in \ mathbb {R } ^ {2 \ fois 500} $, $ b_2 \ in \ mathbb {R} ^ {2} $. Vous pouvez donc voir pourquoi augmenter la taille du calque caché augmente également les paramètres.
Paramètres du train
Entraîner les paramètres signifie rechercher les paramètres ($ W_1 $, $ b_1 $, $ W_2 $, $ b_2 $) qui minimisent la valeur d'erreur sur les données d'entraînement. Alors, comment définissez-vous la valeur d'erreur? La fonction qui mesure la valeur d'erreur est appelée la fonction de perte. Pour Softmax, la fonction de perte couramment utilisée [Minimize Cross Entropy](https://ja.wikipedia.org/wiki/%E4%BA%A4%E5%B7%AE%E3%82%A8%E3 Leads% 83% B3% E3% 83% 88% E3% 83% AD% E3% 83% 94% E3% 83% BC) (également connu sous le nom de probabilité log négative). S'il y a N données d'apprentissage et qu'il y a une classe C, la fonction de perte de la valeur prédite $ \ hat {y} $ peut être écrite comme suit pour la valeur de réponse correcte y.

Cette méthode peut sembler compliquée, mais son rôle est aussi simple que d'ajouter les données d'apprentissage ensemble et d'ajouter la valeur à Loss lorsque la classe est prédite par erreur. Par conséquent, plus les deux distributions de probabilité de la valeur prédite $ \ hat {y} $ et de la valeur de réponse correcte y sont éloignées, plus la perte est grande. Par conséquent, rechercher un paramètre qui minimise la perte équivaut à maximiser la probabilité des données d'apprentissage.
Utilisez Gradient Descent pour calculer la valeur de perte minimale. Cette fois, je mènerai une descente de gradient par lots simple (le taux d'apprentissage est constant), mais [descente de gradient probabiliste](https://ja.wikipedia.org/wiki/%E7%A2%BA%E7%8E%87% E7% 9A% 84% E5% 8B% BE% E9% 85% 8D% E9% 99% 8D% E4% B8% 8B% E6% B3% 95) et la descente de gradient en mini-lots serait plus pratique. Il est également plus pratique de réduire progressivement le taux d'apprentissage.
En entrée, les paramètres de descente de gradient ($ \ frac {\ partial {L}} {\ partial {W_1}} $, $ \ frac {\ partial {L}} {\ partial {b_1}} $, $ \ frac { Calculer la pente de la fonction Loss (valeur différentielle du vecteur) pour \ partial {L}} {\ partial {W_2}} $, $ \ frac {\ partial {L}} {\ partial {b_2}} $) est nécessaire. Utilisez l'algorithme de rétro-propagation pour calculer cette pente. Cet algorithme est un moyen efficace de calculer la pente à partir de la sortie. Ceux qui sont intéressés par ce commentaire mathématique sont ici et [ici](http://cs231n.github.io/optimization- Veuillez lire l'explication en 2 /).
En utilisant la rétro-propagation, ce qui suit est vrai.

En fait, écrivez le code
Finissons les connaissances académiques jusqu'à présent et écrivons réellement le code! Tout d'abord, définissons les variables et les paramètres pour la descente de gradient.
num_examples = len(X) #Taille des données pour la formation
nn_input_dim = 2 #Nombre de dimensions de la couche d'entrée
nn_output_dim = 2 #Nombre de dimensions de la couche de sortie
# Gradient descent parameters (Utilisez des valeurs couramment utilisées)
epsilon = 0.01 #Taux d'apprentissage de la descente de gradient
reg_lambda = 0.01 #Force de régularisation
Écrivons la fonction Loss définie ci-dessus. Vous pouvez diriger cela pour vérifier les performances de votre modèle.
#Fonction d'aide pour calculer toutes les pertes
def calculate_loss(model):
W1, b1, W2, b2 = model['W1'], model['b1'], model['W2'], model['b2']
#Propagation vers l'avant pour le calcul des prévisions
z1 = X.dot(W1) + b1
a1 = np.tanh(z1)
z2 = a1.dot(W2) + b2
exp_scores = np.exp(z2)
probs = exp_scores / np.sum(exp_scores, axis=1, keepdims=True)
#Calculer la perte
corect_logprobs = -np.log(probs[range(num_examples), y])
data_loss = np.sum(corect_logprobs)
#Donnez à la perte un terme de réguratisation(optional)
data_loss += reg_lambda/2 * (np.sum(np.square(W1)) + np.sum(np.square(W2)))
return 1./num_examples * data_loss
Ecrivez une fonction d'assistance pour calculer la couche de sortie. Dirige la propagation vers l'avant décrite ci-dessus et renvoie la probabilité la plus élevée.
# Helper function to predict an output (0 or 1)
def predict(model, x):
W1, b1, W2, b2 = model['W1'], model['b1'], model['W2'], model['b2']
# Forward propagation
z1 = x.dot(W1) + b1
a1 = np.tanh(z1)
z2 = a1.dot(W2) + b2
exp_scores = np.exp(z2)
probs = exp_scores / np.sum(exp_scores, axis=1, keepdims=True)
return np.argmax(probs, axis=1)
Enfin, écrivez le code pour générer le réseau neuronal. Écrivez une descente de gradient par lots en utilisant les différentiels de rétropropagation décrits ci-dessus.
# This function learns parameters for the neural network and returns the model.
# - nn_hdim: Number of nodes in the hidden layer
# - num_passes: Number of passes through the training data for gradient descent
# - print_loss: If True, print the loss every 1000 iterations
def build_model(nn_hdim, num_passes=20000, print_loss=False):
# Initialize the parameters to random values. We need to learn these.
np.random.seed(0)
W1 = np.random.randn(nn_input_dim, nn_hdim) / np.sqrt(nn_input_dim)
b1 = np.zeros((1, nn_hdim))
W2 = np.random.randn(nn_hdim, nn_output_dim) / np.sqrt(nn_hdim)
b2 = np.zeros((1, nn_output_dim))
# This is what we return at the end
model = {}
# Gradient descent. For each batch...
for i in xrange(0, num_passes):
# Forward propagation
z1 = X.dot(W1) + b1
a1 = np.tanh(z1)
z2 = a1.dot(W2) + b2
exp_scores = np.exp(z2)
probs = exp_scores / np.sum(exp_scores, axis=1, keepdims=True)
# Backpropagation
delta3 = probs
delta3[range(num_examples), y] -= 1
dW2 = (a1.T).dot(delta3)
db2 = np.sum(delta3, axis=0, keepdims=True)
delta2 = delta3.dot(W2.T) * (1 - np.power(a1, 2))
dW1 = np.dot(X.T, delta2)
db1 = np.sum(delta2, axis=0)
# Add regularization terms (b1 and b2 don't have regularization terms)
dW2 += reg_lambda * W2
dW1 += reg_lambda * W1
# Gradient descent parameter update
W1 += -epsilon * dW1
b1 += -epsilon * db1
W2 += -epsilon * dW2
b2 += -epsilon * db2
# Assign new parameters to the model
model = { 'W1': W1, 'b1': b1, 'W2': W2, 'b2': b2}
# Optionally print the loss.
# This is expensive because it uses the whole dataset, so we don't want to do it too often.
if print_loss and i % 1000 == 0:
print "Loss after iteration %i: %f" %(i, calculate_loss(model))
return model
Réseau de neurones avec 3 couches cachées
Créons maintenant un réseau avec trois couches cachées.
#Créer un modèle avec un calque caché en trois dimensions
model = build_model(3, print_loss=True)
#Tracer la limite de décision
plot_decision_boundary(lambda x: predict(model, x))
plt.title("Decision Boundary for hidden layer size 3")

J'ai bien reconnu la forme de la lune! Vous pouvez diviser correctement les classes par le réseau neuronal.
Vérifiez la taille compatible du calque caché
Dans ce qui précède, j'ai choisi 3 couches cachées. Ci-dessous, comparons en modifiant le nombre de calques cachés.
plt.figure(figsize=(16, 32))
hidden_layer_dimensions = [1, 2, 3, 4, 5, 20, 50]
for i, nn_hdim in enumerate(hidden_layer_dimensions):
plt.subplot(5, 2, i+1)
plt.title('Hidden Layer size %d' % nn_hdim)
model = build_model(nn_hdim)
plot_decision_boundary(lambda x: predict(model, x))
plt.show()

En regardant la figure ci-dessus, nous avons une bonne compréhension du modèle de données dans le cas de couches cachées de faible dimension (par 3 ou 4). En revanche, il semble qu'il existe un risque de sur-ajustement à des dimensions supérieures. Lorsque cela se produit, c'est comme mémoriser les données dans leur intégralité plutôt que de capturer la vraie forme des données. Si vous dirigez les données de test pour vérifier le modèle, vous devriez être en mesure de prédire avec plus de précision qu'il s'agit d'une couche cachée de faible dimension. Il serait plus (informatiquement) «économique» de choisir la couche de masquage de la bonne taille que de régulariser fortement le surajustement.
Eh bien, cette fois, j'ai essayé de créer un réseau à partir de zéro sans utiliser de bibliothèque. Ensuite, j'expliquerai l'apprentissage profond plus en profondeur en utilisant la bibliothèque de réseau neuronal.
- Rédigé avec Denny Britz, qui écrit le blog wildML
Recommended Posts