I made an N-dimensional matrix operation library Matft with Swift
Introduction
This is the first post. As the title says, I made an N-dimensional matrix operation library ** Matft (https://github.com/jjjkkkjjj/Matft) ** in Swift. Saw. (** Mat ** rix operation, Swi ** ft **, which stands for Matft lol)
The beginning of the matter was a word from a senior at the company, "I want you to write a code to find the inverse matrix of 3 rows and 3 columns in Swift." I thought that Swift would have an N-dimensional matrix operation library like Python's Numpy, but when I looked it up, it wasn't surprising. .. .. The official Accelerate seems to be inconvenient, and the famous surge is up to 2D? It was like. That's why I decided to make my own N-dimensional matrix operation library. (It's completely over-engineered for the code that finds the inverse matrix of 3 rows and 3 columns, but lol)
Furthermore, Matft was created like this. And since it's a big deal, I'm going to share it, and I'm up to the present.
Overview
Since it was basically created after Python's Numpy, the function name and usage are almost the same as Numpy.
Declaration
The declaration creates a multidimensional array with MfArray, which is ndarray.
let a = MfArray([[[ -8, -7, -6, -5],
[ -4, -3, -2, -1]],
[[ 0, 1, 2, 3],
[ 4, 5, 6, 7]]])
print(a)
/*
mfarray =
[[[ -8.0, -7.0, -6.0, -5.0],
[ -4.0, -3.0, -2.0, -1.0]],
[[ 0.0, 1.0, 2.0, 3.0],
[ 4.0, 5.0, 6.0, 7.0]]], type=Float, shape=[2, 2, 4]
*/
Mold
I wanted to support various types, so I prepared a certain type. It is not dtype but MfType.
let a = MfArray([[[ -8, -7, -6, -5],
[ -4, -3, -2, -1]],
[[ 0, 1, 2, 3],
[ 4, 5, 6, 7]]], mftype: .Float)
print(a)
/*
mfarray =
[[[ -8.0, -7.0, -6.0, -5.0],
[ -4.0, -3.0, -2.0, -1.0]],
[[ 0.0, 1.0, 2.0, 3.0],
[ 4.0, 5.0, 6.0, 7.0]]], type=Float, shape=[2, 2, 4]
*/
let aa = MfArray([[[ -8, -7, -6, -5],
[ -4, -3, -2, -1]],
[[ 0, 1, 2, 3],
[ 4, 5, 6, 7]]], mftype: .UInt)
print(aa)
/*
mfarray =
[[[ 4294967288, 4294967289, 4294967290, 4294967291],
[ 4294967292, 4294967293, 4294967294, 4294967295]],
[[ 0, 1, 2, 3],
[ 4, 5, 6, 7]]], type=UInt, shape=[2, 2, 4]
*/
//Above output is same as numpy!
/*
>>> np.arange(-8, 8, dtype=np.uint32).reshape(2,2,4)
array([[[4294967288, 4294967289, 4294967290, 4294967291],
[4294967292, 4294967293, 4294967294, 4294967295]],
[[ 0, 1, 2, 3],
[ 4, 5, 6, 7]]], dtype=uint32)
The type list is defined by the following Enum type.
- To tell the truth, since it is saved as
FloatorDoublebehind the scenes, ʻUInt` will overflow if the value is large. However, I don't think there is any problem in practical use.
public enum MfType: Int{
case None // Unsupportted
case Bool
case UInt8
case UInt16
case UInt32
case UInt64
case UInt
case Int8
case Int16
case Int32
case Int64
case Int
case Float
case Double
case Object // Unsupported
}
Indexing
Slices like ʻa [:, :: -1]in Numpy are also implemented with~ <. (Initially, it was implemented with ~, but ~ 2` etc. will be bit Not ... It was stupid)
I also implemented a negative index like -1. (This may have been the hardest ...)
let a = Matft.mfarray.arange(start: 0, to: 27, by: 1, shape: [3,3,3])
print(a)
/*
mfarray =
[[[ 0, 1, 2],
[ 3, 4, 5],
[ 6, 7, 8]],
[[ 9, 10, 11],
[ 12, 13, 14],
[ 15, 16, 17]],
[[ 18, 19, 20],
[ 21, 22, 23],
[ 24, 25, 26]]], type=Int, shape=[3, 3, 3]
*/
print(a[2,1,0])
// 21
print(a[1~<3]) //same as a[1:3] for numpy
/*
mfarray =
[[[ 9, 10, 11],
[ 12, 13, 14],
[ 15, 16, 17]],
[[ 18, 19, 20],
[ 21, 22, 23],
[ 24, 25, 26]]], type=Int, shape=[2, 3, 3]
*/
print(a[-1~<-3])
/*
mfarray =
[], type=Int, shape=[0, 3, 3]
*/
print(a[~<~<-1]) // print(a[~<<-1])With an alias~<<Is also equivalent
/*
mfarray =
[[[ 18, 19, 20],
[ 21, 22, 23],
[ 24, 25, 26]],
[[ 9, 10, 11],
[ 12, 13, 14],
[ 15, 16, 17]],
[[ 0, 1, 2],
[ 3, 4, 5],
[ 6, 7, 8]]], type=Int, shape=[3, 3, 3]*/
List of other functions
The following is a list of specific functions. Since the main calculation is left to Accelerate, I think that the calculation time is secured to some extent.
\ * Means that method also exists. In other words, if ʻa is MfArray, you can use ʻa.shallowcopy ().
--Generating system
| Matft | Numpy |
|---|---|
| *Matft.shallowcopy | *numpy.copy |
| *Matft.deepcopy | copy.deepcopy |
| Matft.nums | numpy.ones * N |
| Matft.arange | numpy.arange |
| Matft.eye | numpy.eye |
| Matft.diag | numpy.diag |
| Matft.vstack | numpy.vstack |
| Matft.hstack | numpy.hstack |
| Matft.concatenate | numpy.concatenate |
--Conversion system
| Matft | Numpy |
|---|---|
| *Matft.astype | *numpy.astype |
| *Matft.transpose | *numpy.transpose |
| *Matft.expand_dims | *numpy.expand_dims |
| *Matft.squeeze | *numpy.squeeze |
| *Matft.broadcast_to | *numpy.broadcast_to |
| *Matft.conv_order | *numpy.ascontiguousarray |
| *Matft.flatten | *numpy.flatten |
| *Matft.flip | *numpy.flip |
| *Matft.clip | *numpy.clip |
| *Matft.swapaxes | *numpy.swapaxes |
| *Matft.moveaxis | *numpy.moveaxis |
| *Matft.sort | *numpy.sort |
| *Matft.argsort | *numpy.argsort |
--File related save is incomplete.
| Matft | Numpy |
|---|---|
| Matft.file.loadtxt | numpy.loadtxt |
| Matft.file.genfromtxt | numpy.genfromtxt |
--Computational system
The second line is the operator.
| Matft | Numpy |
|---|---|
| Matft.add + |
numpy.add + |
| Matft.sub - |
numpy.sub - |
| Matft.div / |
numpy.div . |
| Matft.mul * |
numpy.multiply * |
| Matft.inner *+ |
numpy.inner n/a |
| Matft.cross *^ |
numpy.cross n/a |
| Matft.matmul *& |
numpy.matmul @ |
| Matft.equal === |
numpy.equal == |
| Matft.not_equal !== |
numpy.not_equal != |
| Matft.allEqual == |
numpy.array_equal n/a |
| Matft.neg - |
numpy.negative - |
--Elementary function system
| Matft | Numpy |
|---|---|
| Matft.math.sin | numpy.sin |
| Matft.math.asin | numpy.asin |
| Matft.math.sinh | numpy.sinh |
| Matft.math.asinh | numpy.asinh |
| Matft.math.sin | numpy.cos |
| Matft.math.acos | numpy.acos |
| Matft.math.cosh | numpy.cosh |
| Matft.math.acosh | numpy.acosh |
| Matft.math.tan | numpy.tan |
| Matft.math.atan | numpy.atan |
| Matft.math.tanh | numpy.tanh |
| Matft.math.atanh | numpy.atanh |
Since it is troublesome, I will omit it. .. .. Lol See here
--Statistical system
| Matft | Numpy |
|---|---|
| *Matft.stats.mean | *numpy.mean |
| *Matft.stats.max | *numpy.max |
| *Matft.stats.argmax | *numpy.argmax |
| *Matft.stats.min | *numpy.min |
| *Matft.stats.argmin | *numpy.argmin |
| *Matft.stats.sum | *numpy.sum |
| Matft.stats.maximum | numpy.maximum |
| Matft.stats.minimum | numpy.minimum |
--Linear algebra
| Matft | Numpy |
|---|---|
| Matft.linalg.solve | numpy.linalg.solve |
| Matft.linalg.inv | numpy.linalg.inv |
| Matft.linalg.det | numpy.linalg.det |
| Matft.linalg.eigen | numpy.linalg.eig |
| Matft.linalg.svd | numpy.linalg.svd |
| Matft.linalg.polar_left | scipy.linalg.polar |
| Matft.linalg.polar_right | scipy.linalg.polar |
| Matft.linalg.normlp_vec | scipy.linalg.norm |
| Matft.linalg.normfro_mat | scipy.linalg.norm |
| Matft.linalg.normnuc_mat | scipy.linalg.norm |
Installation
Added support for SwiftPM, CocoaPod and Carthage.
SwiftPM
- Import
- Project > Build Setting > +
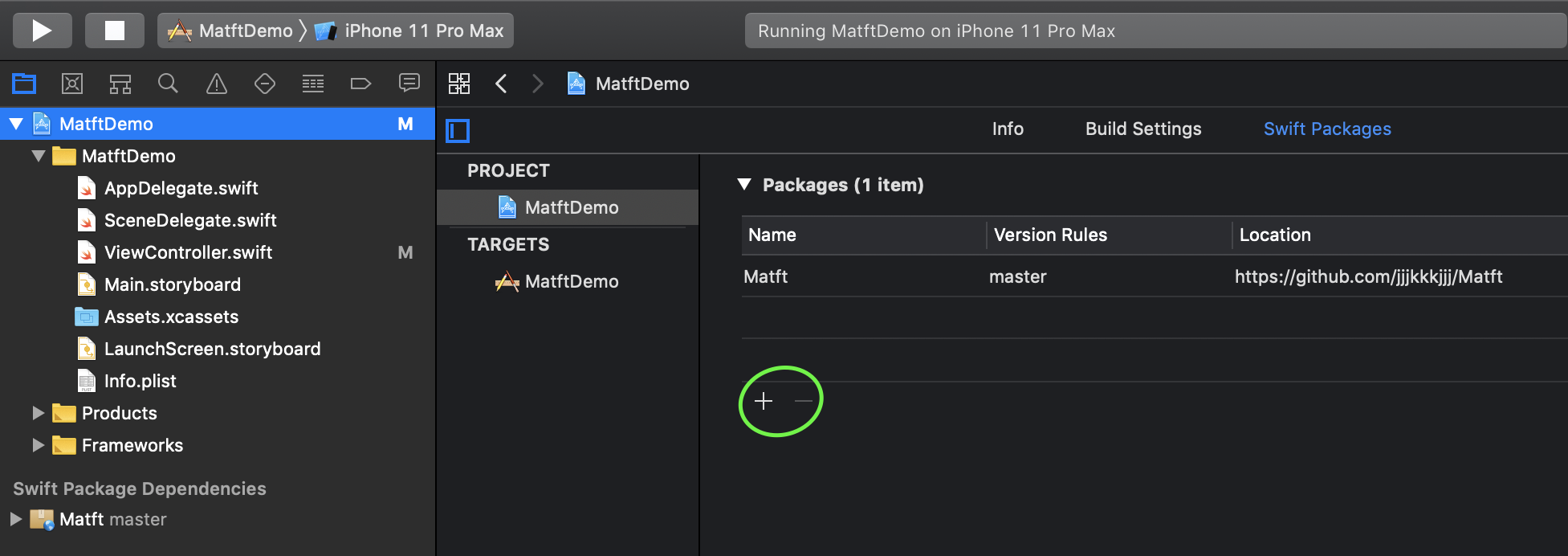 --Select as appropriate
--Select as appropriate
 --Update
--Update - File >Swift Packages >Update to Latest Package versions
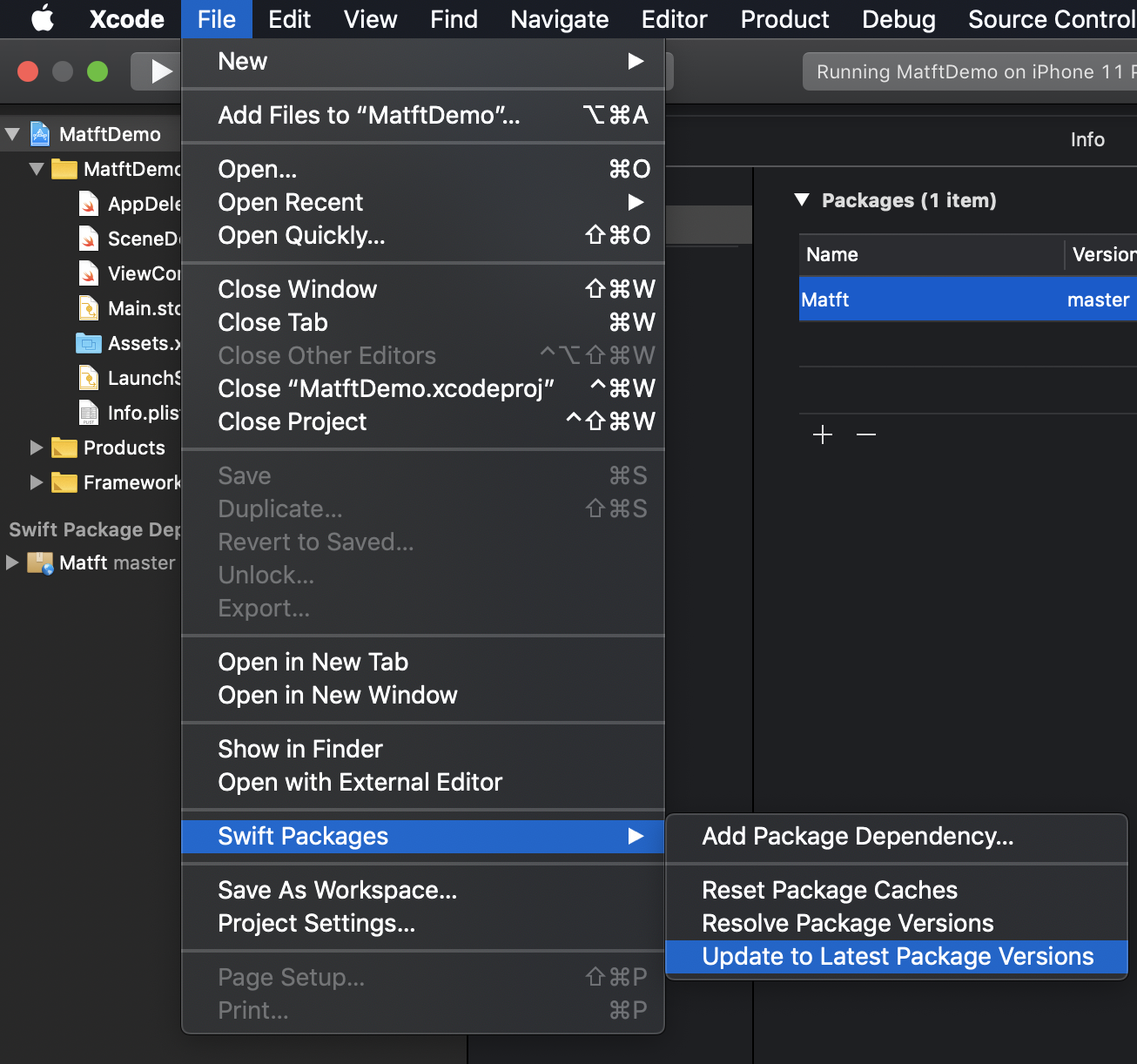
- Project > Build Setting > +
CocoaPods
--Create Podfile (ignore if it already exists)
pod init
--Added pod'Matft' to Podfile
target 'your project' do
pod 'Matft'
end
--Installation
pod install
Carthage (unconfirmed)
-Create in Cartfile and read.
echo 'github "realm/realm-cocoa"' > Cartfile
carthage update ###or append '--platform ios'
--It's OK if you load the completed Matft.framework into the project.
Performance
I said that the calculation is guaranteed because I leave it to Accelerate, but I calculated the speed only by addition. If I have time, I will investigate other functions. .. ..
| case | Matft | Numpy |
|---|---|---|
| 1 | 1.14ms | 962 µs |
| 2 | 4.20ms | 5.68 ms |
| 3 | 4.17ms | 3.92 ms |
- Matft
func testPefAdd1() {
do{
let a = Matft.mfarray.arange(start: 0, to: 10*10*10*10*10*10, by: 1, shape: [10,10,10,10,10,10])
let b = Matft.mfarray.arange(start: 0, to: -10*10*10*10*10*10, by: -1, shape: [10,10,10,10,10,10])
self.measure {
let _ = a+b
}
/*
'-[MatftTests.ArithmeticPefTests testPefAdd1]' measured [Time, seconds] average: 0.001, relative standard deviation: 23.418%, values: [0.001707, 0.001141, 0.000999, 0.000969, 0.001029, 0.000979, 0.001031, 0.000986, 0.000963, 0.001631]
1.14ms
*/
}
}
func testPefAdd2(){
do{
let a = Matft.arange(start: 0, to: 10*10*10*10*10*10, by: 1, shape: [10,10,10,10,10,10])
let b = a.transpose(axes: [0,3,4,2,1,5])
let c = a.T
self.measure {
let _ = b+c
}
/*
'-[MatftTests.ArithmeticPefTests testPefAdd2]' measured [Time, seconds] average: 0.004, relative standard deviation: 5.842%, values: [0.004680, 0.003993, 0.004159, 0.004564, 0.003955, 0.004200, 0.003998, 0.004317, 0.003919, 0.004248]
4.20ms
*/
}
}
func testPefAdd3(){
do{
let a = Matft.arange(start: 0, to: 10*10*10*10*10*10, by: 1, shape: [10,10,10,10,10,10])
let b = a.transpose(axes: [1,2,3,4,5,0])
let c = a.T
self.measure {
let _ = b+c
}
/*
'-[MatftTests.ArithmeticPefTests testPefAdd3]' measured [Time, seconds] average: 0.004, relative standard deviation: 16.815%, values: [0.004906, 0.003785, 0.003702, 0.005981, 0.004261, 0.003665, 0.004083, 0.003654, 0.003836, 0.003874]
4.17ms
*/
}
}
- Numpy
In [1]:
import numpy as np
#import timeit
a = np.arange(10**6).reshape((10,10,10,10,10,10))
b = np.arange(0, -10**6, -1).reshape((10,10,10,10,10,10))
#timeit.timeit("b+c", repeat=10, globals=globals())
%timeit -n 10 a+b
962 µs ± 273 µs per loop (mean ± std. dev. of 7 runs, 10 loops each)
In [2]:
a = np.arange(10**6).reshape((10,10,10,10,10,10))
b = a.transpose((0,3,4,2,1,5))
c = a.T
#timeit.timeit("b+c", repeat=10, globals=globals())
%timeit -n 10 b+c
5.68 ms ± 1.45 ms per loop (mean ± std. dev. of 7 runs, 10 loops each)
In [3]:
a = np.arange(10**6).reshape((10,10,10,10,10,10))
b = a.transpose((1,2,3,4,5,0))
c = a.T
#timeit.timeit("b+c", repeat=10, globals=globals())
%timeit -n 10 b+c
3.92 ms ± 897 µs per loop (mean ± std. dev. of 7 runs, 10 loops each)
What I personally like
- name --Multiple type support --Numpy Possa
- Indexing --Points corresponding to Row Major and Column Major (here) --Algorithm to pass to Accelerate (here)
Subtleties
--There is still overhead
--Even though I implemented flag that holds the Order of MfArray, there are some parts that are uselessly copied.
--The generating system is converting from ʻArraytoMfArray` (I want to use vDSP)
--Protocol is not used well
Finally
I made it on a whim, but I got something better than I expected. There may be a better library just because of my lack of search power, but I would be grateful if you could give it a try. (Environment-dependent checks have not been completed, so please do not hesitate to contact us ...) Anyway, it was a good study. Thank you very much.
reference
numpy scipy Accelerate Write NDArray in Swift (I referred to the test case.)
Recommended Posts