traduction google de http://scikit-learn.org/stable/tutorial/statistical_inference/unsupervised_learning.html Table des matières du didacticiel scikit-learn 0.18 Tableau du didacticiel d'apprentissage statistique pour le traitement des données scientifiques Page précédente du didacticiel

Apprentissage non supervisé: recherche de représentation des données

Regroupement: regrouper les observations

Problèmes résolus par le clustering

Étant donné un ensemble de données d'iris, si vous avez trois types d'iris, mais que vous n'avez pas accès pour étiqueter le taxonomiste, vous pouvez essayer une tâche de clustering: observe dans des groupes bien séparés appelés clusters. Diviser.

Clustering moyen K

Notez qu'il existe de nombreux critères de clustering et algorithmes associés. L'algorithme de clustering le plus simple est K Mean.

>>> from sklearn import cluster, datasets
>>> iris = datasets.load_iris()
>>> X_iris = iris.data
>>> y_iris = iris.target

>>> k_means = cluster.KMeans(n_clusters=3)
>>> k_means.fit(X_iris) 
KMeans(algorithm='auto', copy_x=True, init='k-means++', ...
>>> print(k_means.labels_[::10])
[1 1 1 1 1 0 0 0 0 0 2 2 2 2 2]
>>> print(y_iris[::10])
[0 0 0 0 0 1 1 1 1 1 2 2 2 2 2]

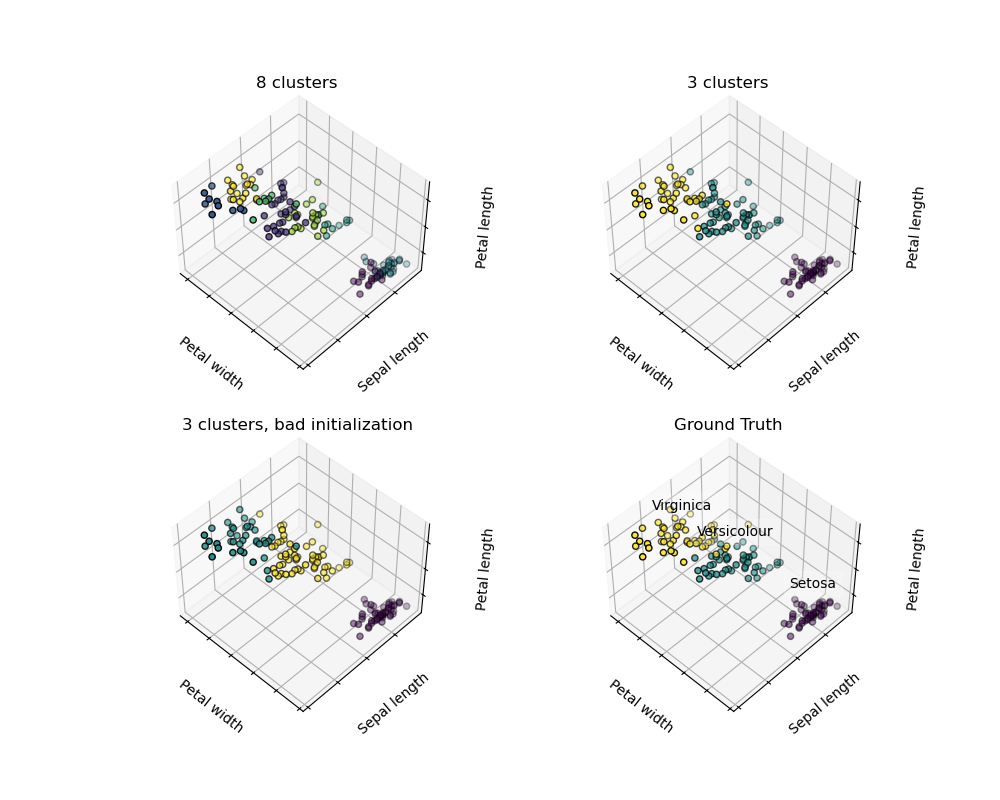
Avertissement Il n'y a absolument aucune garantie que la vérité sur terre sera rétablie. Premièrement, il est difficile de choisir le bon nombre de clusters. Deuxièmement, l'algorithme est sensible aux valeurs initiales et scicit-learn utilise quelques astuces pour atténuer ce problème, mais il peut tomber dans un minimum local.

Mauvaise initialisation	8 grappes	Ground truth

** Ne pas surinterpréter les résultats du clustering **

Exemple d'application: quantification vectorielle

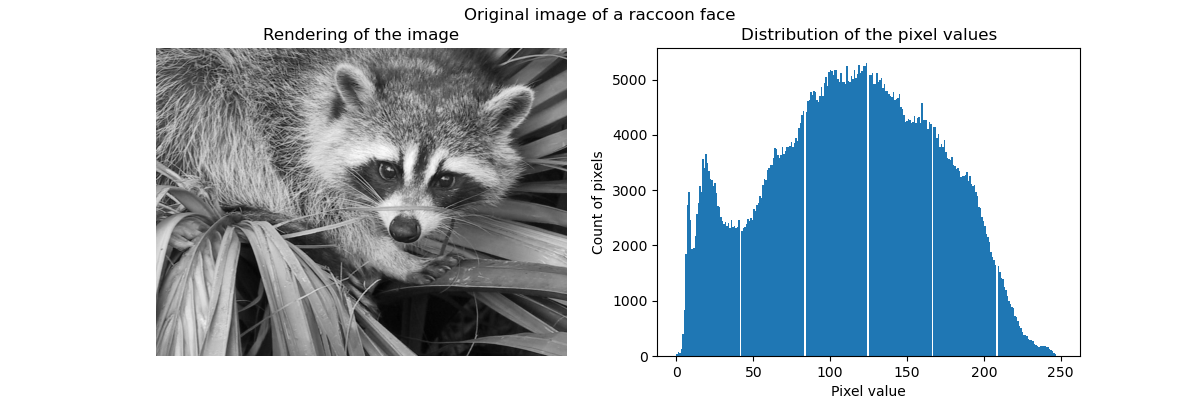
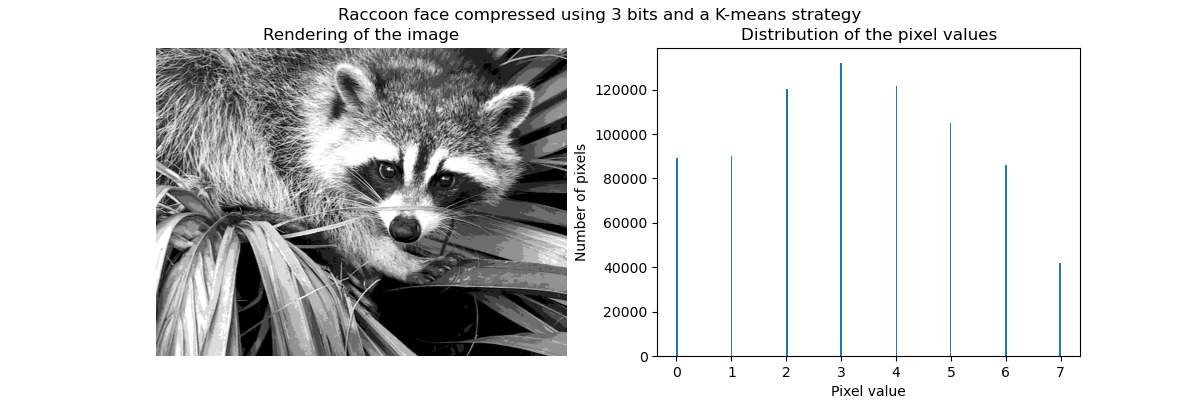
En général, le clustering et les K Means peuvent être considérés comme un moyen de choisir quelques exemples de compression d'informations. Ce problème est parfois appelé quantification vectorielle. Par exemple, cela peut être utilisé pour postériser une image:

>>> import scipy as sp
>>> try:
...    face = sp.face(gray=True)
... except AttributeError:
...    from scipy import misc
...    face = misc.face(gray=True)
>>> X = face.reshape((-1, 1)) # We need an (n_sample, n_feature) array
>>> k_means = cluster.KMeans(n_clusters=5, n_init=1)
>>> k_means.fit(X) 
KMeans(algorithm='auto', copy_x=True, init='k-means++', ...
>>> values = k_means.cluster_centers_.squeeze()
>>> labels = k_means.labels_
>>> face_compressed = np.choose(labels, values)
>>> face_compressed.shape = face.shape

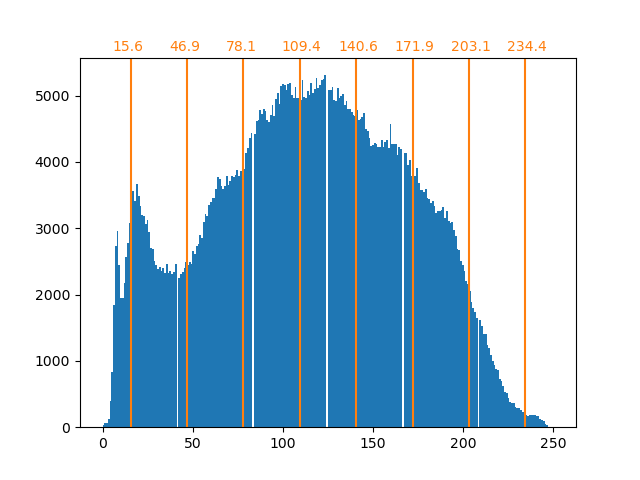
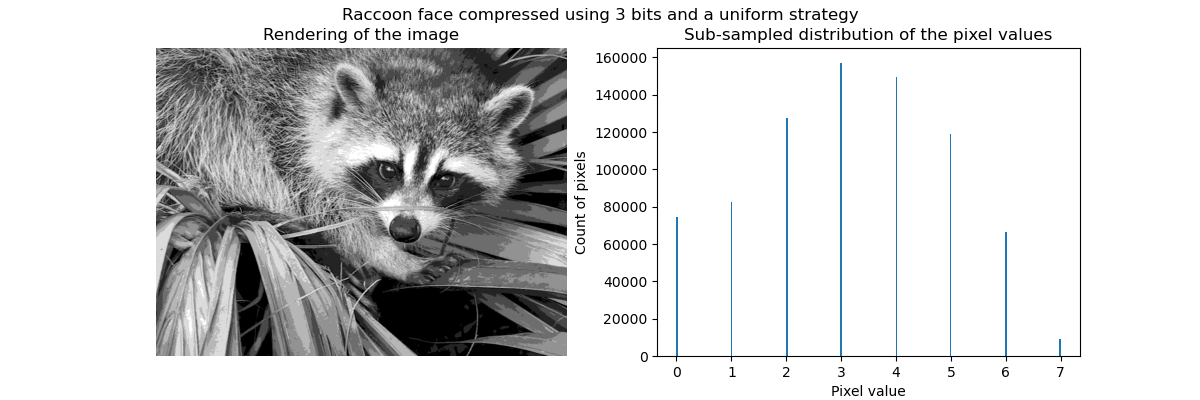
Image brute	K-Quantification	Poubelle égale	Histogramme d'image

Clustering cohésif hiérarchique: méthode de Ward

La méthode de clustering hiérarchique est un type d'analyse de cluster qui vise à construire une hiérarchie de clusters. En général, les différentes approches de cette technologie

** Agrégat ** - Approche ascendante: chaque observation commence par son propre cluster, et les clusters sont fusionnés de manière intensive de manière à minimiser les critères de liaison. Cette approche est particulièrement intéressante lorsque les grappes d'intérêt sont constituées de très peu d'observations. Avec un grand nombre de clusters, il est beaucoup plus efficace que la moyenne k.
** Ramifié ** - Approche descendante: toutes les observations commencent dans un seul cluster et sont divisées de manière itérative lorsque vous vous déplacez dans la hiérarchie. Pour estimer un grand nombre de clusters, cette approche est lente et statistiquement malveillante (pour toutes les observations commençant par un cluster et se fractionnant de manière récursive).

Clustering avec connectivité contrainte

Le clustering agrégé vous permet de spécifier les échantillons à regrouper en créant un graphique de connexion. Le graphe dans scikit est représenté par sa matrice adjacente. Des matrices clairsemées sont souvent utilisées. Ceci est utile, par exemple, lors du regroupement d'images pour obtenir la zone connectée (également appelée composant connecté).

import matplotlib.pyplot as plt

from sklearn.feature_extraction.image import grid_to_graph
from sklearn.cluster import AgglomerativeClustering
from sklearn.utils.testing import SkipTest
from sklearn.utils.fixes import sp_version

if sp_version < (0, 12):
    raise SkipTest("Skipping because SciPy version earlier than 0.12.0 and "
                   "thus does not include the scipy.misc.face() image.")


###############################################################################
# Generate data
try:
    face = sp.face(gray=True)
except AttributeError:
    # Newer versions of scipy have face in misc
    from scipy import misc
    face = misc.face(gray=True)

# Resize it to 10% of the original size to speed up the processing
face = sp.misc.imresize(face, 0.10) / 255.

Agrégation de fonctionnalités

Nous avons trouvé que la malédiction des nombres dimensionnels, c'est-à-dire, peut être utilisée pour atténuer les observations inadéquates par rapport au nombre de caractéristiques. Une autre approche consiste à intégrer des fonctionnalités similaires. Agglomération de fonctionnalités. Cette approche peut être réalisée par un clustering orienté fonctionnalité, c'est-à-dire un clustering de données transposées.

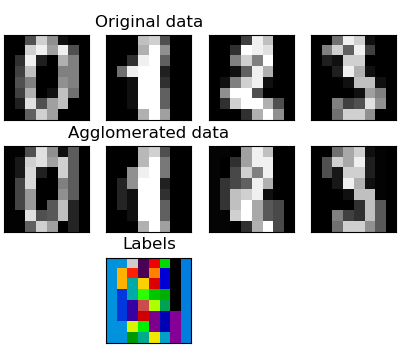
>>> digits = datasets.load_digits()
>>> images = digits.images
>>> X = np.reshape(images, (len(images), -1))
>>> connectivity = grid_to_graph(*images[0].shape)

>>> agglo = cluster.FeatureAgglomeration(connectivity=connectivity,
...                                      n_clusters=32)
>>> agglo.fit(X) 
FeatureAgglomeration(affinity='euclidean', compute_full_tree='auto',...
>>> X_reduced = agglo.transform(X)

>>> X_approx = agglo.inverse_transform(X_reduced)
>>> images_approx = np.reshape(X_approx, images.shape)

Méthode `transform` et méthode ʻinverse_transform`

Certains estimateurs exposent la méthode transform, par exemple pour réduire le nombre de dimensions dans l'ensemble de données.

Décomposition: du signal au composant et au chargement

Composants et chargement

Si X est nos données multivariées, le problème que nous essayons de résoudre est de les réécrire avec différents critères d'observation: nous aimons charger $ L $ et $ X = LC $. Je veux apprendre un ensemble de composants $ C $. Il existe différents critères de sélection des composants.

Analyse en composantes principales: PCA

L'analyse principale (PCA) (http://scikit-learn.org/stable/modules/decomposition.html#pca) sélectionne les composantes continues qui décrivent la dispersion maximale du signal.

Le groupe de points qui couvre les observations ci-dessus est très plat dans une direction. L'une des trois entités univariées peut être calculée presque exactement à l'aide des deux autres fonctions. PCA trouve des directions où les données ne sont pas plates PCA peut être utilisé pour transformer des données afin de réduire la dimension des données en les projetant dans un sous-espace majeur.

>>> #Créer un signal avec seulement deux dimensions valides
>>> x1 = np.random.normal(size=100)
>>> x2 = np.random.normal(size=100)
>>> x3 = x1 + x2
>>> X = np.c_[x1, x2, x3]

>>> from sklearn import decomposition
>>> pca = decomposition.PCA()
>>> pca.fit(X)
PCA(copy=True, iterated_power='auto', n_components=None, random_state=None,
  svd_solver='auto', tol=0.0, whiten=False)
>>> print(pca.explained_variance_)  
[  2.18565811e+00   1.19346747e+00   8.43026679e-32]

>>> #Comme vous pouvez le voir, seuls les deux premiers composants sont utiles
>>> pca.n_components = 2
>>> X_reduced = pca.fit_transform(X)
>>> X_reduced.shape
(100, 2)

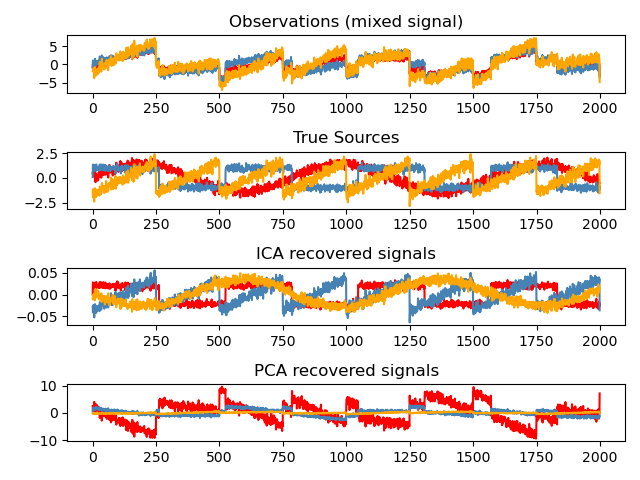
Analyse indépendante des composants: ICA

Independent Component Analysis (ICA) (http://scikit-learn.org/stable/modules/decomposition.html#ica) sélectionne les composants de sorte que la distribution du composant contienne le maximum d'informations indépendantes. .. ** Non-Gauss ** Les signaux indépendants peuvent être restaurés.

>>> # Generate sample data
>>> time = np.linspace(0, 10, 2000)
>>> s1 = np.sin(2 * time)  # Signal 1 : sinusoidal signal
>>> s2 = np.sign(np.sin(3 * time))  # Signal 2 : square signal
>>> S = np.c_[s1, s2]
>>> S += 0.2 * np.random.normal(size=S.shape)  # Add noise
>>> S /= S.std(axis=0)  # Standardize data
>>> # Mix data
>>> A = np.array([[1, 1], [0.5, 2]])  # Mixing matrix
>>> X = np.dot(S, A.T)  # Generate observations

>>> # Compute ICA
>>> ica = decomposition.FastICA()
>>> S_ = ica.fit_transform(X)  # Get the estimated sources
>>> A_ = ica.mixing_.T
>>> np.allclose(X,  np.dot(S_, A_) + ica.mean_)
True

[Français] didacticiel scikit-learn 0.18 Didacticiel d'apprentissage statistique pour le traitement des données scientifiques Apprentissage non supervisé: recherche de représentation des données