introduction

Est-ce que vous renforcez l'apprentissage? L'apprentissage par renforcement est une technologie amusante qui peut être appliquée aux robots, aux jeux tels que Go et Shogi et aux systèmes de dialogue.

L'apprentissage intensifié est un cadre de contrôle d'apprentissage qui s'adapte à l'environnement par essais et erreurs. Dans l'apprentissage supervisé, la sortie correcte a été donnée à l'entrée pour l'apprentissage. Dans l'apprentissage renforcé, au lieu de donner la sortie correcte pour l'entrée, une valeur d'évaluation scalaire appelée «récompense» qui évalue le bien ou le mal d'une série d'actions est donnée, et l'apprentissage est effectué en utilisant cela comme un indice. Le cadre de l'apprentissage par renforcement est présenté ci-dessous.

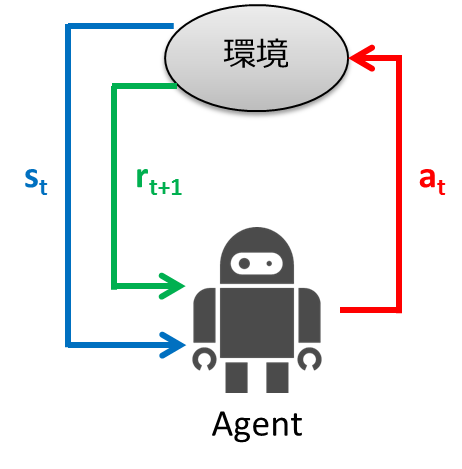
L'agent observe l'état de l'environnement $ s_t $ au temps $ t $
Déterminez l'action $ a_t $ à partir de l'état observé
L'agent prend des mesures
L'environnement passe au nouvel état $ s_ {t + 1} $
Gagnez $ r_ {t + 1} $ selon la transition
Apprendre
Répétez à partir de l'étape 1

Le but de l'apprentissage intensif est d'obtenir une cartographie état-action (politique) qui maximise les gains (récompenses cumulatives) que les agents obtiennent.

Dans l'apprentissage renforcé, le cadre ci-dessus est modélisé par les processus de décision de Markov (MDP) et l'algorithme d'apprentissage est pris en compte. Dans cet article, nous expliquerons le renforcement de l'apprentissage séparément en théorie et en pratique. Dans la section théorie, nous expliquerons MDP et les algorithmes d'apprentissage, et dans la section pratique, nous implémenterons ce qui a été expliqué dans la section théorie en utilisant le langage de programmation Python. Nous vous recommandons de les lire dans l'ordre, mais si vous dites "Komake Kota est bon!", Sautez la section théorie et lisez la section pratique.

Théorie

Tout d'abord, je vais expliquer la théorie de l'apprentissage par renforcement avec des exemples. Ici, après avoir expliqué la définition du problème de l'exemple, le processus de décision de Markov sera expliqué. Maintenant que vous comprenez le processus de décision Markov, parlons de la façon de l'apprendre.

Problème de réglage

Maintenant, pour expliquer MDP, considérons le monde labyrinthe suivant.

Les règles du monde du labyrinthe sont les suivantes:

L'agent est dans une grille
L'agent ne peut pas traverser le mur (gris)
Les agents ne travaillent pas toujours comme ils le souhaitent
80% de chances de se déplacer correctement, 10% de chances de se déplacer vers la gauche dans la direction que vous aviez l'intention de déplacer, 10% de chances de se déplacer vers la droite
S'il y a un mur sur lequel vous souhaitez vous déplacer, restez-y
L'agent reçoit une récompense à chaque fois
Lorsque vous atteignez l'objectif (coffre au trésor) ou le piège (explosion), le jeu se termine et vous revenez à la position de départ.

Nous expliquerons la transition stochastique plus en détail à l'aide de la figure ci-dessous.

Ici, le robot essaie de monter. À ce stade, il y a 80% de chances de monter, mais 10% de chances de se déplacer vers la gauche et les 10% restants de se déplacer vers la droite. Les probabilités de transition sont indiquées dans le tableau ci-dessous.

s'	P(s' \mid s_1, a)
s_2	0.1
s_3	0.8
s_4	0.1

Processus de décision de Markov (MDP)

Maintenant, avez-vous compris la configuration du problème? Maintenant que nous savons, nous allons modéliser le problème avec MDP.

MDP est défini par l'ensemble de 4 termes suivant

M = (S, A, T, R)

Qu'est-ce que chacun?

Ensemble d'états: $ s \ in S $
Ensemble d'actions: $ a \ in A $
Fonction de transition: $ T (s, a, s ') \ sim P (s' \ mid s, a) $
Fonction de récompense: $ R (s) $, $ R (s, a) $, $ R (s, a, s ') $

Appliquons chacun aux paramètres de problème expliqués ci-dessus.

L'ensemble d'états représente l'ensemble d'états que l'environnement peut prendre, et dans le cas de l'exemple, il représente toutes les cellules de la grille.
Un ensemble d'actions est un type d'action qu'un agent peut entreprendre. Dans le cas de l'exemple, il existe quatre types d'agents car ils peuvent se déplacer vers le haut, le bas, la gauche et la droite.
La fonction de transition est la probabilité de transition vers l'état suivant $ s '$ lorsque l'action $ a $ est effectuée dans un état $ s $. Comme expliqué dans la figure ci-dessus.
La récompense est la valeur reçue de l'environnement à la suite d'une nouvelle transition qui détermine l'action à entreprendre à partir de l'état observé. J'expliquerai en détail plus tard.

Le but de ce MDP est d'apprendre des stratégies d'action qui maximisent les gains (= récompenses cumulatives). Cette stratégie d'action s'appelle ** politique **.

Un peu plus sur la politique

L'objectif de MDP est d'obtenir la meilleure politique $ \ pi ^ *: S \ rightarrow A $. Une politique peut être considérée comme une fonction qui mappe les états aux actions. La politique vous dit quoi faire dans chaque situation. Des politiques optimales maximisent également les gains attendus.

Jetons un coup d'œil au changement de politique optimal lors de la modification des récompenses obtenues au moment de la transition. Cette figure montre le changement de politique lorsque la récompense obtenue de la transition d'état est progressivement réduite (la pénalité est augmentée). La politique apprend de l'idée de maximiser les gains escomptés qui peuvent être obtenus. Par conséquent, si la pénalité due à la transition d'état est petite, il essaiera de viser le but même s'il détourne, et si la pénalité est grande, il faudra une stratégie pour terminer le jeu rapidement. Des images fixes sont également disponibles pour une comparaison facile.

Un peu plus sur les récompenses

Jusqu'à présent, j'ai dit que je maximiserai les récompenses cumulatives afin d'apprendre la politique. Puisque vous pouvez obtenir la récompense $ R (s_t) $ à chaque fois, la récompense cumulative peut être exprimée comme suit.

\begin{align}
U([s_0, s_1, s_2,\ldots]) &= R(s_0) + R(s_1) + R(s_2) + \cdots \\
    &= \sum_{t=0}^{\infty}R(s_t)
\end{align}

Vous pouvez utiliser cette simple récompense cumulative, mais pour plusieurs raisons, vous pouvez actualiser la future récompense avec le facteur de remise $ \ gamma (0 \ leq \ gamma <1) $ comme indiqué dans la formule ci-dessous. Des récompenses cumulatives sont utilisées. Cela vous donnera plus de poids sur ce que vous obtenez maintenant que sur ce que vous obtiendrez à l'avenir.

\begin{align}
U([s_0, s_1, s_2,\ldots]) &= R(s_0) + \gamma R(s_1) + \gamma^2 R(s_2) + \cdots \\
    &= \sum_{t=0}^{\infty}\gamma^t R(s_t)
\end{align}

Les raisons de l'utilisation de ces remises sont les suivantes.

La valeur ne diverge pas du point de vue du calcul
Dans un environnement réel, il n'est pas raisonnable de considérer toutes les récompenses de la série chronologique avec le même poids, car l'environnement peut changer avec le temps.

Comment trouver la meilleure politique

Jusqu'à présent, nous connaissons le modèle appelé MDP. La question qui reste est de savoir comment trouver la meilleure politique. Dans ce qui suit, nous expliquerons la méthode d'itération de valeur et le Q-Learning en tant qu'algorithmes pour trouver la politique optimale.

Itération de valeur

La méthode d'itération de valeur calcule le gain attendu de l'état $ s $ lorsque vous continuez à prendre des mesures optimales. La raison pour laquelle on considère la valeur attendue du gain obtenu est qu'une transition probabiliste est effectuée.

Une fois que vous connaissez ce gain attendu, vous connaissez la valeur que vous obtiendrez à l'avenir à partir de l'état actuel de $ s $, et vous devriez être en mesure de choisir des actions qui maximisent cette valeur. La valeur est calculée par la fonction de valeur d'état suivante. Cela semble compliqué, mais en bref, il ne s'agit que de calculer la récompense cumulative (attendue).

U(s) = R(s) + \gamma \max_a\sum_{s'} P(s' \mid s,a) U(s')

Il existe un calcul non linéaire appelé max dans cette équation, et il est difficile de le résoudre avec une matrice ou similaire. Par conséquent, des calculs itératifs sont effectués pour mettre à jour progressivement la valeur. C'est la raison du nom de la méthode d'itération de valeur. L'algorithme d'itération de valeur est illustré ci-dessous. Le montant du calcul estO(|S|^2 |A|)est.

Initialisez $ U (s) $ à une valeur appropriée (telle que zéro) pour tous les états $ s $

Calculez la formule suivante pour tous les $ U (s) $ et mettez à jour les valeurs

U(s) \leftarrow R(s) + \gamma \max_a\sum_{s'} P(s' \mid s,a) U(s')

 > 3. Répétez l'étape 2 jusqu'à ce que les valeurs convergent

 Il y a une partie pour calculer max dans la formule ci-dessus, mais il faut enregistrer l'action a dont la valeur est la valeur maximale. Par conséquent, il est difficile de comprendre la politique optimale (comportement) uniquement avec $ U (s) $. Par conséquent, la fonction Q suivante est introduite. Également appelée fonction de valeur d'action.

```math
Q^*(s,a) = R(s) + \gamma \sum_{s'} P(s' \mid s,a) \max_{a'}Q^*(s', a')

** $ Q ^ * (s, a) $ ** représente la valeur attendue de la récompense actualisée cumulative si vous continuez à appliquer la politique optimale après avoir sélectionné l'action a dans ** state $ s $. Il y a une différence entre $ U (s) $ et $ Q ^ * (s, a) $ s'ils ne contiennent que la valeur maximale dans chaque état ou la valeur de chaque action. Par conséquent, la valeur Q maximale dans l'état s est égale à $ U (s) $, et l'action a avec cette valeur Q est l'action optimale. La figure ci-dessous est l'image.

La méthode d'itération de valeur lors de l'utilisation de la fonction Q est la suivante.

Initialisez $ Q ^ * (s, a) $ à une valeur appropriée (telle que zéro) pour tous les états $ s $

Calculez la formule suivante pour tout $ Q ^ * (s, a) $ et mettez à jour les valeurs

Q^(s,a) \leftarrow R(s) + \gamma \sum_{s'} P(s' \mid s,a) \max_{a'}Q^(s', a')


 > 3. Répétez l'étape 2 jusqu'à ce que les valeurs convergent


 À ce stade, il est facile de trouver la meilleure politique $ \ pi ^ * (s) $. Il est calculé ci-dessous.

```math
\pi^*(s) = arg\max_{a}Q^*(s,a)

Exemple de calcul

Comme c'est un gros problème, essayons de calculer la valeur de la place rouge ci-dessous. Utilisez la formule suivante pour le calcul.

U(s) \leftarrow R(s) + \gamma \max_a\sum_{s'} P(s' \mid s,a) U(s')

$ \ Gamma = 0,5 $, $ R (s) = -0,04 $, la probabilité de transition est de 0,8 dans la direction que vous voulez aller, et de 0,1 de chaque côté.

Dans les conditions ci-dessus, la valeur dans la zone rouge est ...

\begin{align}
U(s) &= -0.04 + 0.5 \cdot (0.8 \cdot 1 + 0.1 \cdot 0 + 0.1 \cdot 0)\\
&= -0.04 + 0.4\\
&= 0.36
\end{align}

Est requis.

Q-Learning Maintenant, je suis soulagé que la politique optimale soit requise par la méthode de répétition de valeur. Ce n'est pas le grossiste. Qu'est-ce qui ne va pas?

Jusqu'à présent, nous connaissions la probabilité de transition d'état. Cependant, compte tenu du problème réel, il est rare que la probabilité de transition d'état soit connue. Imaginez les échecs ou le shogi. La probabilité de transition d'une carte (état) à une autre (autre état) est-elle donnée à l'avance? Vous ne l'avez pas reçu, non? Dans de tels cas, la méthode d'itération de valeur ne peut pas être utilisée.

C'est là que Q-Learning, qui peut être considéré comme une version d'apprentissage améliorée de la méthode de répétition de valeur, sort. Dans Q-Learning Calculez l'estimation $ \ hat {Q} ^ {\ *} (s_t, a_t) $ pour $ \ hat {Q} ^ {\ *} (s, a) $. En utilisant Q-Learning, vous pouvez apprendre la politique optimale même dans des situations où vous ne connaissez pas la probabilité de transition. L'algorithme Q-Learning est le suivant.

Initialisez $ \ hat Q ^ * (s_t, a_t) $ avec une valeur appropriée

Mise à jour de l'estimation de la valeur d'action à l'aide de la formule suivante. Cependant, $ \ alpha $ est le taux d'apprentissage de $ 0 \ leq \ alpha \ leq 1 $.

\hat Q^(s_t, a_t) \leftarrow \hat Q^(s_t, a_t) + \alpha \Bigl[ r_{t+1} + \gamma \max_{a \in A}\hat Q^(s_{t+1}, a) - \hat Q^(s_t, a_t) \Bigr]

 > 3. Avancer le pas de temps $ t $ à $ t + 1 $ et revenir à 2

 Vous pouvez obtenir le $ Q ^ * (s, a) $ optimal en répétant ce calcul.

<!--
 En comparant la formule de mise à jour de la méthode d'itération de valeur (version de fonction Q) et la formule de mise à jour de Q-Learning, la probabilité de transition $ P (s '\ mid s, a) $ est calculée pour la fonction Q dans la méthode d'itération de valeur. Bien qu'il soit utilisé, il n'est pas utilisé car il est inconnu dans la situation où Q-Learning est utilisé. En effectuant des calculs itératifs
-->

# Édition pratique
 Voyons ce qui se passe si nous faisons ce que nous avons expliqué ci-dessus en Python.

## Méthode de répétition des valeurs
 Le premier est la méthode d'itération de valeur.
 La méthode d'itération de valeur est basée sur le code propre (mdp.py) dans [UC Berkeley](https://github.com/aimacode/aima-python).

### Classe MDP
 Tout d'abord, de MDP qui est la classe de base. Héritez et créez une classe GridMDP.

```python
class MDP:

    def __init__(self, init, actlist, terminals, gamma=.9):
        self.init = init
        self.actlist = actlist
        self.terminals = terminals
        if not (0 <= gamma < 1):
            raise ValueError("An MDP must have 0 <= gamma < 1")
        self.gamma = gamma
        self.states = set()
        self.reward = {}

    def R(self, state):
	return self.reward[state]

    def T(self, state, action):
        raise NotImplementedError

    def actions(self, state):
        if state in self.terminals:
            return [None]
        else:
            return self.actlist

La méthode \ _ \ _ init \ _ \ _ reçoit les paramètres suivants:

init: état initial.
actlist: actions qui peuvent être entreprises dans chaque état.
terminaux: Liste des états terminés
gamma: facteur de remise

La méthode ** R ** renvoie la récompense pour chaque état. La méthode ** T ** est un modèle de transition. Bien qu'il s'agisse ici d'une méthode abstraite, lorsque l'action $ a $ est effectuée dans l'état $ s $, elle retourne une liste de probabilités de transition vers l'état suivant et un tuple (probabilité, s ') de l'état suivant. Nous allons l'implémenter avec Grid MDP. La méthode ** actions ** renvoie une liste d'actions pouvant être entreprises dans chaque état.

Classe GridMDP

La classe GridMDP est une classe concrète de la classe de base MDP. Cette classe est pour exprimer le monde du labyrinthe expliqué dans l'exemple.

class GridMDP(MDP):

    def __init__(self, grid, terminals, init=(0, 0), gamma=.9):
        grid.reverse()  # because we want row 0 on bottom, not on top                                                                                                  
        MDP.__init__(self, init, actlist=orientations,
                     terminals=terminals, gamma=gamma)
        self.grid = grid
        self.rows = len(grid)
        self.cols = len(grid[0])
        for x in range(self.cols):
            for y in range(self.rows):
                self.reward[x, y] = grid[y][x]
                if grid[y][x] is not None:
                    self.states.add((x, y))

    def T(self, state, action):
        if action is None:
            return [(0.0, state)]
        else:
            return [(0.8, self.go(state, action)),
                    (0.1, self.go(state, turn_right(action))),
                    (0.1, self.go(state, turn_left(action)))]

    def go(self, state, direction):
        state1 = vector_add(state, direction)
        return state1 if state1 in self.states else state

    def to_grid(self, mapping):
        return list(reversed([[mapping.get((x, y), None)
                               for x in range(self.cols)]
                              for y in range(self.rows)]))

    def to_arrows(self, policy):
        chars = {(1, 0): '>', (0, 1): '^', (-1, 0): '<', (0, -1): 'v', None: '.'}
        return self.to_grid({s: chars[a] for (s, a) in policy.items()})

La méthode \ _ \ _ init \ _ \ _ reçoit presque les mêmes arguments que la classe MDP, sauf qu'elle reçoit l'argument de grille. La grille stocke les récompenses pour chaque état. Passez-le comme suit. Aucun ne représente un mur.

GridMDP([[-0.04, -0.04, -0.04, +1],
        [-0.04, None,  -0.04, -1],
        [-0.04, -0.04, -0.04, -0.04]],
        terminals=[(3, 2), (3, 1)])

La méthode ** go ** renvoie l'état lors du déplacement dans la direction spécifiée. La méthode ** T ** est telle que décrite dans MDP. Il est en fait mis en œuvre ici. Les méthodes ** to_grid ** et ** to_arrows ** sont des méthodes d'affichage.

Implémentation de la méthode d'itération de valeur

def value_iteration(mdp, epsilon=0.001):
    U1 = {s: 0 for s in mdp.states}
    R, T, gamma = mdp.R, mdp.T, mdp.gamma
    while True:
        U = U1.copy()
        delta = 0
        for s in mdp.states:
            U1[s] = R(s) + gamma * max([sum([p * U[s1] for (p, s1) in T(s, a)])
                                        for a in mdp.actions(s)])
            delta = max(delta, abs(U1[s] - U[s]))
        if delta < epsilon * (1 - gamma) / gamma:
            return U


def best_policy(mdp, U):
    pi = {}
    for s in mdp.states:
        pi[s] = argmax(mdp.actions(s), key=lambda a: expected_utility(a, s, U, mdp))
    return pi


def expected_utility(a, s, U, mdp):
    return sum([p * U[s1] for (p, s1) in mdp.T(s, a)])

La fonction ** value_iteration ** prend une instance de GridMDP comme entrée et une petite valeur epsilon et renvoie U (s) dans chaque état comme sortie. Cela ressemble à ce qui suit.

>> value_iteration(sequential_decision_environment)
{(0, 0): 0.2962883154554812,
 (0, 1): 0.3984432178350045,
 (0, 2): 0.5093943765842497,
 (1, 0): 0.25386699846479516,
 (1, 2): 0.649585681261095,
 (2, 0): 0.3447542300124158,
 (2, 1): 0.48644001739269643,
 (2, 2): 0.7953620878466678,
 (3, 0): 0.12987274656746342,
 (3, 1): -1.0,
 (3, 2): 1.0}

Ensuite, en passant le résultat calculé par la fonction value_iteration à la fonction ** best_policy **, la politique optimale est obtenue.

Courir

Voici le code à essayer. Cependant, tel quel, cela ne fonctionne pas car certains modules nécessaires n'ont pas été importés. Par conséquent, si vous voulez réellement l'exécuter, clonez le référentiel ici et exécutez-le.

sequential_decision_environment = GridMDP([[-0.04, -0.04, -0.04, +1],
                                           [-0.04, None,  -0.04, -1],
                                           [-0.04, -0.04, -0.04, -0.04]],
                                          terminals=[(3, 2), (3, 1)])

pi = best_policy(sequential_decision_environment, value_iteration(sequential_decision_environment, .01))

print_table(sequential_decision_environment.to_arrows(pi))

À la suite de la mise en œuvre, les politiques suivantes peuvent être obtenues.

>   >      >   .
^   None   ^   .
^   >      ^   <

Q-Learning Il n'y a pas de bosse, c'est comme un ressort

Veuillez écrire Q-Learning lorsque vous avez de la force physique.

Matériel de référence

Vidéo de conférence Udacity. Les lettres sont difficiles à lire, mais l'histoire est facile à comprendre.

Machine Learning: Reinforcement Learning

Matériaux japonais

Matériel anglais

Matériel qui explique l'itération de la valeur d'une manière facile à comprendre avec des chiffres

Documents de référence lors de la mise en œuvre de l'itération de valeur

Expansion de formule polie de la fonction de valeur

Reinforcement Learning Searching for optimal policies I:Bellman equations and optimal policies

Apprentissage amélioré à partir de Python