100 Language Processing Knock 2020 Chapitre 8: Neural Net

L'autre jour, 100 Language Processing Knock 2020 a été publié. Je ne travaille moi-même sur le langage naturel que depuis un an, et je ne connais pas les détails, mais je vais résoudre tous les problèmes et les publier afin d'améliorer mes compétences techniques.

Tout doit être exécuté sur le notebook jupyter, et les restrictions de l'énoncé du problème peuvent être brisées de manière pratique. Le code source est également sur github. Oui.

Le chapitre 7 est ici.

L'environnement est Python 3.8.2 et Ubuntu 18.04.

Chapitre 8: Réseau neuronal

Mettre en œuvre un modèle de catégorisation avec un réseau de neurones basé sur la catégorisation des articles de presse abordés au chapitre 6. Dans ce chapitre, utilisez des plates-formes d'apprentissage automatique telles que PyTorch, TensorFlow et Chainer.

Utilisez PyTorch.

70. Caractéristiques par somme de vecteurs de mots

Je souhaite convertir les données d'entraînement, les données de vérification et les données d'évaluation construites dans le problème 50 en matrices et vecteurs. Par exemple, pour les données d'apprentissage, nous aimerions créer une matrice $ X $ dans laquelle les vecteurs de caractéristiques de tous les cas sont arrangés et une matrice (vecteur) $ Y $ dans laquelle les étiquettes de réponse correctes sont arrangées.

X = \begin{pmatrix} \boldsymbol{x}_1 \ \boldsymbol{x}_2 \ \dots \ \boldsymbol{x}_n \ \end{pmatrix} \in \mathbb{R}^{n \times d}, Y = \begin{pmatrix} y_1 \ y_2 \ \dots \ y_n \ \end{pmatrix} \in \mathbb{N}^{n}

>
 > Ici, $ n $ est le nombre de cas de données d'apprentissage, et $ \ boldsymbol x_i \ in \ mathbb {R} ^ d $ et $ y_i \ in \ mathbb N $ sont respectivement $ i \ in \ {1. \ dots, n \} Représente le vecteur de caractéristiques et l'étiquette correcte du $ th cas.
 > Cette fois, il y a quatre catégories: «affaires», «science et technologie», «divertissement» et «santé». Si $ \ mathbb N_4 $ représente un nombre naturel (y compris $ 0 $) inférieur à $ 4 $, l'étiquette de réponse correcte $ y_i $ peut dans tous les cas être représentée par $ y_i \ in \ mathbb N_4 $.
 > Dans ce qui suit, le nombre de types d'étiquettes est représenté par $ L $ ($ L = 4 $ dans cette tâche de classification).
>
 > Le vecteur de caractéristiques $ \ boldsymbol x_i $ du cas $ i $ th est calculé par l'équation suivante.
>
> $$\boldsymbol x_i = \frac{1}{T_i} \sum_{t=1}^{T_i} \mathrm{emb}(w_{i,t})$$
>
 > Ici, le cas $ i $ ème est $ T_i $ (titre d'article) chaînes de mots $ (w_ {i, 1}, w_ {i, 2}, \ dots, w_ {i, T_i}) $ \\ mathrm {emb} (w) \ in \ mathbb {R} ^ d $ est un vecteur de mot (le nombre de dimensions est $ d $) correspondant au mot $ w $. Autrement dit, $ \ boldsymbol x_i $ est l'en-tête d'article du $ i $ ème cas exprimé par la moyenne des vecteurs des mots contenus dans l'en-tête. Cette fois, le mot vecteur téléchargé à la question 60 doit être utilisé. Puisque nous avons utilisé un vecteur de mot de dimension 300 $, $ d = 300 $.
 > L'étiquette $ y_i $ du cas $ i $ ème est définie comme suit.
>
>```math
y_i = \begin{cases}
0 & (\mbox{article}\boldsymbol x_i\mbox{Si appartient à la catégorie "Entreprise"}) \\
1 & (\mbox{article}\boldsymbol x_i\mbox{Fait partie de la catégorie "Science et technologie"}) \\
2 & (\mbox{article}\boldsymbol x_i\mbox{Si appartient à la catégorie "Divertissement"}) \\
3 & (\mbox{article}\boldsymbol x_i\mbox{Si appartient à la catégorie «santé»}) \\
\end{cases}

S'il existe une correspondance univoque entre le nom de la catégorie et le numéro d'étiquette, la correspondance ne doit pas nécessairement être comme indiqué dans la formule ci-dessus.

En vous basant sur les spécifications ci-dessus, créez la matrice / vecteur suivant et enregistrez-le dans un fichier.

• Matrice des caractéristiques des données d'entraînement: $ X_ {\ rm train} \ in \ mathbb {R} ^ {N_t \ times d} $
• Vecteur d'étiquette de données d'entraînement: $ Y_ {\ rm train} \ in \ mathbb {N} ^ {N_t} $
• Matrice des caractéristiques des données de validation: $ X_ {\ rm valide} \ in \ mathbb {R} ^ {N_v \ times d} $
• Vecteur d'étiquette de données de validation: $ Y_ {\ rm valide} \ in \ mathbb {N} ^ {N_v} $
• Matrice des caractéristiques des données d'évaluation: $ X_ {\ rm test} \ in \ mathbb {R} ^ {N_e \ times d} $
• Vecteur d'étiquette de données d'évaluation: $ Y_ {\ rm test} \ in \ mathbb {N} ^ {N_e} $

Notez que $ N_t, N_v et N_e $ sont respectivement le nombre de cas de données d'apprentissage, le nombre de cas de données de vérification et le nombre de cas de données d'évaluation.

L'énoncé du problème est long et il est difficile de corriger TeX.

code

import re
import spacy

Divisez en mots.

code

nlp = spacy.load('en')
categories = ['b', 't', 'e', 'm']
category_names = ['business', 'science and technology', 'entertainment', 'health']

code

def tokenize(x):
    x = re.sub(r'\s+', ' ', x)
    x = nlp.make_doc(x)
    x = [d.text for d in x]
    return x

def read_feature_dataset(filename):
    with open(filename) as f:
        dataset = f.read().splitlines()
    dataset = [line.split('\t') for line in dataset]
    dataset_t = [categories.index(line[0]) for line in dataset]
    dataset_x = [tokenize(line[1]) for line in dataset]
    return dataset_x, dataset_t

code

train_x, train_t = read_feature_dataset('data/train.txt')
valid_x, valid_t = read_feature_dataset('data/valid.txt')
test_x, test_t = read_feature_dataset('data/test.txt')

Convertissez en un vecteur d'entités.

code

import torch
from gensim.models import KeyedVectors

code

model = KeyedVectors.load_word2vec_format('../GoogleNews-vectors-negative300.bin.gz', binary=True)

code

def sent_to_vector(sent):
    lst = [torch.tensor(model[token]) for token in sent if token in model]
    return sum(lst) / len(lst)

def dataset_to_vector(dataset):
    return torch.stack([sent_to_vector(x) for x in dataset])

code

train_v = dataset_to_vector(train_x)
valid_v = dataset_to_vector(valid_x)
test_v = dataset_to_vector(test_x)

code

train_v[0]

production

tensor([ 9.0576e-02,  5.4932e-02, -7.7393e-02,  1.1810e-01, -3.8849e-02,
        -2.6074e-01, -6.4484e-02,  3.2715e-02,  1.1792e-01, -3.4363e-02,
        -1.5137e-02, -1.7090e-02,  7.2632e-02,  1.0742e-02,  1.1194e-01,
         5.8945e-02,  1.6275e-01,  1.5393e-01,  7.0496e-02, -1.5210e-01,
         2.8320e-02,  1.1719e-02,  1.9702e-01, -1.5610e-02, -2.3438e-02,
         1.8921e-02,  2.8687e-02, -2.3438e-02,  2.3315e-02, -5.7480e-02,
         2.1973e-03, -1.0449e-01, -9.7534e-02, -1.3694e-01,  1.6144e-01,
        -2.6062e-02,  3.1250e-02,  1.9482e-01, -1.0788e-01,  7.2571e-02,
        -1.3916e-02,  1.1121e-01,  7.0801e-03, -4.1016e-02, -1.9580e-01,
         1.7334e-02,  1.0986e-02, -6.9485e-03,  9.2773e-02,  7.2205e-02,
         6.8298e-02, -5.3589e-02, -1.7447e-01,  1.0245e-01, -8.6426e-02,
        -9.0942e-03, -1.7212e-01, -1.3789e-01, -1.0355e-01,  1.9226e-02,
         1.0620e-02,  9.7626e-02, -5.1147e-02,  1.1371e-01,  3.5156e-02,
        -4.8523e-03, -7.1960e-02,  1.1841e-01, -1.0974e-01,  1.2878e-01,
        -7.3273e-02,  5.3711e-02,  9.6313e-02, -9.0950e-02,  4.3335e-02,
        -4.7424e-02, -3.0518e-02,  5.2856e-02,  3.7842e-02,  2.2559e-01,
         4.0161e-02, -2.3822e-01, -1.3531e-01, -3.8513e-02, -1.1475e-02,
        -7.3242e-02, -1.9324e-01,  1.9553e-01,  1.0870e-01,  1.5405e-01,
         2.8793e-02, -1.9226e-01,  3.1952e-02, -1.0471e-01,  4.9561e-02,
         6.5918e-03, -5.6793e-02,  1.8628e-01, -5.5908e-02, -9.8999e-02,
        -2.1448e-01, -1.6602e-02,  6.7627e-02,  2.1149e-02, -6.8970e-02,
         2.3804e-03, -2.1729e-02, -9.1599e-02, -8.7585e-02, -1.1963e-01,
        -8.7555e-02,  6.1768e-02, -1.6205e-02,  2.9572e-02,  1.2207e-04,
         1.3300e-01,  1.6541e-02, -1.3672e-01,  1.4978e-01, -4.8828e-03,
        -2.6172e-01,  3.9093e-02,  1.4761e-01,  1.3745e-01,  8.6670e-03,
        -1.0797e-01,  8.3801e-02,  3.2690e-01, -6.9336e-02,  6.8115e-02,
         1.0571e-01, -1.2269e-01, -1.4209e-01,  7.7923e-02, -1.6113e-02,
        -6.8039e-02,  1.2909e-02, -4.9911e-02,  2.0142e-01,  9.5764e-02,
         8.1078e-02, -2.6733e-02, -1.4606e-01, -1.0449e-01,  7.1014e-02,
         9.4604e-03,  9.6436e-02, -3.3386e-02, -6.5552e-02, -4.0009e-02,
         2.0976e-01, -9.5825e-02,  1.2494e-01, -1.1230e-02,  1.3062e-02,
         1.8829e-02, -1.7525e-01, -1.6845e-01, -3.0334e-02, -5.6152e-02,
        -2.3193e-02, -8.4961e-02,  4.6021e-02,  1.5533e-01, -2.4780e-02,
        -1.7255e-01, -2.9472e-02, -3.2959e-03, -3.2166e-02,  1.1292e-01,
        -5.0537e-02,  6.0730e-02,  1.8042e-01, -2.6678e-01,  6.5601e-02,
        -2.4567e-01, -4.1382e-02, -2.4902e-02, -7.3853e-02,  3.8330e-02,
        -3.5229e-01, -4.8477e-02,  7.8522e-02,  2.4719e-03, -1.1414e-02,
        -8.9661e-02, -2.4341e-01,  4.9133e-02, -2.7954e-02,  9.2651e-02,
        -4.8340e-02, -5.2063e-02,  5.5817e-02, -3.7842e-03, -1.6852e-01,
         9.8267e-03,  2.1698e-02, -6.5107e-02,  9.8053e-02, -3.6621e-03,
        -2.2009e-01,  1.1389e-01,  5.0537e-02, -1.4322e-01, -8.2336e-02,
        -5.0507e-02, -2.2461e-02, -9.4971e-02, -1.0464e-01, -2.0959e-01,
        -1.2964e-01, -1.0208e-02, -4.0894e-03, -1.4893e-02, -4.9637e-02,
         6.3507e-02, -8.5968e-02,  2.3340e-01,  1.2207e-01, -1.6663e-01,
        -1.6541e-01,  6.9924e-02,  2.4414e-02, -3.3630e-02, -2.2583e-02,
        -2.1289e-01,  8.4106e-02,  1.1916e-01, -1.9623e-02, -3.2654e-02,
        -3.2394e-02,  1.5515e-01, -7.9224e-02, -9.1919e-02, -6.3782e-03,
        -3.6926e-02,  8.0456e-02, -4.5288e-02,  1.9531e-02,  7.4951e-02,
        -8.0195e-02, -2.5232e-01,  1.0986e-01, -1.2573e-01, -1.0083e-01,
         2.0972e-01,  1.3380e-03,  2.2363e-01, -6.7322e-02, -6.3477e-02,
        -2.1167e-01,  5.0659e-03, -3.2227e-02, -2.0752e-02,  2.2107e-01,
        -2.4243e-01,  1.4246e-01,  1.4465e-01, -2.0691e-01, -1.0516e-01,
        -1.0327e-01,  1.6028e-01, -1.4748e-02, -1.9310e-02,  2.3193e-02,
         1.5234e-01,  2.2034e-02, -8.0872e-04, -8.7729e-02,  5.9967e-02,
        -2.6306e-02,  1.3672e-01,  1.5301e-02,  6.3965e-02,  1.9131e-02,
        -5.8695e-02,  1.4355e-01, -9.6710e-02,  7.2235e-02, -1.0620e-02,
         6.1523e-02, -1.2626e-01,  3.3813e-02, -2.1973e-03, -1.3843e-01,
        -1.3458e-01,  5.4447e-02, -2.0325e-01,  1.2244e-01,  4.3335e-02,
        -3.1372e-02, -1.9659e-01, -1.7270e-01,  2.9846e-02, -5.8533e-02,
         6.7017e-02,  1.6748e-01,  1.1859e-01,  1.2134e-01, -1.7578e-02])

Enregistrer comme cornichon.

code

import pickle

code

train_t = torch.tensor(train_t).long()
valid_t = torch.tensor(valid_t).long()
test_t = torch.tensor(test_t).long()

code

with open('data/train.feature.pickle', 'wb') as f:
    pickle.dump(train_v, f)
with open('data/train.label.pickle', 'wb') as f:
    pickle.dump(train_t, f)
    
with open('data/valid.feature.pickle', 'wb') as f:
    pickle.dump(valid_v, f)
with open('data/valid.label.pickle', 'wb') as f:
    pickle.dump(valid_t, f)
    
with open('data/test.feature.pickle', 'wb') as f:
    pickle.dump(test_v, f)
with open('data/test.label.pickle', 'wb') as f:
    pickle.dump(test_t, f)

71. Prédiction par réseau neuronal monocouche

Lisez la matrice enregistrée à la question 70 et effectuez les calculs suivants sur les données d'entraînement.

Cependant, $ {\ rm softmax} $ est la fonction softmax, $ X_ {[1: 4]} \ in \ mathbb {R} ^ {4 \ times d} $ est le vecteur de caractéristiques $ \ boldsymbol x_1, \ boldsymbol x_2 , \ Boldsymbol x_3, \ boldsymbol x_4 $ sont disposés verticalement.

La matrice $ W \ in \ mathbb {R} ^ {d \ times L} $ est la matrice de poids du réseau neuronal monocouche, qui peut être initialisée avec une valeur aléatoire (apprise dans le problème 73 et plus tard). .. Notez que $ \ hat {\ boldsymbol y_1} \ in \ mathbb {N} ^ L $ est un vecteur représentant la probabilité d'appartenir à chaque catégorie lorsque le cas $ x_1 $ est classé par la matrice non apprise $ W $. De même, $ \ hat {Y} \ in \ mathbb {N} ^ {n \ times L} $ exprime la probabilité d'appartenir à chaque catégorie comme une matrice pour les exemples de données d'apprentissage $ x_1, x_2, x_3, x_4 $. faites.

Je pense que l'intention de l'interrogateur est probablement de faire quelque chose comme torch.empty (). Normal_ () puis F.linear (), mais ceux qui le savent ont déjà nn. Je pense qu'il est normal d'hériter de Module. En plus du problème suivant, je sens l'intention de la question de faire en quelque sorte des gens qui ne savent pas ce qu'est la différenciation automatique.

code

import torch.nn as nn

code

class Perceptron(nn.Module):
    def __init__(self, v_size, c_size):
        super().__init__()
        self.fc = nn.Linear(v_size, c_size, bias = False)
        nn.init.xavier_normal_(self.fc.weight)
        
    def forward(self, x):
        x = self.fc(x)
        return x

code

model = Perceptron(300, 4)

code

x = model(train_v[0])
x = torch.softmax(x, dim=-1)
x

production

tensor([0.2450, 0.2351, 0.2716, 0.2483], grad_fn=<SoftmaxBackward>)

code

x = model(train_v[:4])
x = torch.softmax(x, dim=-1)
x

production

tensor([[0.2450, 0.2351, 0.2716, 0.2483],
        [0.2323, 0.2387, 0.2765, 0.2525],
        [0.2093, 0.2120, 0.2750, 0.3037],
        [0.2200, 0.2427, 0.2623, 0.2751]], grad_fn=<SoftmaxBackward>)

Il a une distribution de probabilité appropriée.

72. Calcul de la perte et de la pente

Calculez la perte d'entropie croisée et le gradient pour la matrice $ W $ pour le cas $ x_1 $ et l'ensemble de cas $ x_1, x_2, x_3, x_4 $ des données d'apprentissage. Pour un certain cas $ x_i $, la perte est calculée par l'équation suivante.

Cependant, la perte d'entropie croisée pour l'ensemble de cas est la moyenne des pertes pour chaque cas inclus dans l'ensemble.

code

criterion = nn.CrossEntropyLoss()

code

y = model(train_v[:1])
t = train_t[:1]
loss = criterion(y, t)
model.zero_grad()
loss.backward()
print('perte:', loss.item())
print('Pente')
print(model.fc.weight.grad)

production

perte: 1.2622126340866089
Pente
tensor([[ 0.0229,  0.0139, -0.0196,  ...,  0.0300,  0.0307, -0.0044],
        [ 0.0219,  0.0133, -0.0187,  ...,  0.0287,  0.0294, -0.0043],
        [ 0.0201,  0.0122, -0.0172,  ...,  0.0263,  0.0270, -0.0039],
        [-0.0649, -0.0394,  0.0555,  ..., -0.0850, -0.0870,  0.0126]])

Si vous oubliez zero_grad (), le gradient s'accumulera à l'infini et ce sera étrange.

code

model.zero_grad()
model.fc.weight.grad

production

tensor([[0., 0., 0.,  ..., 0., 0., 0.],
        [0., 0., 0.,  ..., 0., 0., 0.],
        [0., 0., 0.,  ..., 0., 0., 0.],
        [0., 0., 0.,  ..., 0., 0., 0.]])

code

y = model(train_v[:4])
t = train_t[:4]
loss = criterion(y, t)
model.zero_grad()
loss.backward()
print('perte:', loss.item())
print('Pente')
print(model.fc.weight.grad)

production

perte: 1.3049677610397339
Pente
tensor([[ 0.0044,  0.0014, -0.0114,  ...,  0.0090,  0.0150, -0.0018],
        [-0.0008,  0.0036, -0.0066,  ...,  0.0076,  0.0111, -0.0007],
        [ 0.0038,  0.0008, -0.0114,  ...,  0.0082,  0.0145, -0.0017],
        [-0.0074, -0.0059,  0.0295,  ..., -0.0248, -0.0406,  0.0042]])

73. Apprentissage par la méthode probabiliste de descente de gradient

Apprenez la matrice $ W $ en utilisant la méthode SGD (Stochastic Gradient Descent). L'apprentissage peut être achevé selon une norme appropriée (par exemple, «Fin dans 100 époques»).

Au moment de la régression logistique, nous avons utilisé la méthode quasi-Newton pour toutes les données, mais cette fois il s'agit d'une descente de gradient stochastique, nous allons donc mélanger le jeu de données et l'extraire petit à petit.

La classe Dataset est un enfant qui contient des données. Lorsque __getitem__ reçoit l'entier de l'index des données, les données de cette adresse sont renvoyées.

code

class Dataset(torch.utils.data.Dataset):
    def __init__(self, x, t):
        self.x = x
        self.t = t
        self.size = len(x)
    
    def __len__(self):
        return self.size
            
    def __getitem__(self, index):
        return {
            'x':self.x[index],
            't':self.t[index],
        }

La classe Sampler est un enfant qui récupère plusieurs index d'un ensemble de données en lots et divise l'ensemble de données en lots.

code

class Sampler(torch.utils.data.Sampler):
    def __init__(self, dataset, width, shuffle=False):
        self.dataset = dataset
        self.width = width
        self.shuffle = shuffle
        if not shuffle:
            self.indices = torch.arange(len(dataset))
    
    def __iter__(self):
        if self.shuffle:
            self.indices = torch.randperm(len(self.dataset))
        index = 0
        while index < len(self.dataset):
            yield self.indices[index : index + self.width]
            index += self.width

Vous pouvez mélanger et récupérer l'ensemble de données en passant l'ensemble de données et l'échantillonneur à torch.utils.data.DataLoader.

code

def gen_loader(dataset, width, sampler=Sampler, shuffle=False, num_workers=8):
    return torch.utils.data.DataLoader(
        dataset, 
        batch_sampler = sampler(dataset, width, shuffle),
        num_workers = num_workers,
    )

Préparez un chargeur de données avec des données d'entraînement et des données de vérification.

code

train_dataset = Dataset(train_v, train_t)
valid_dataset = Dataset(valid_v, valid_t)
test_dataset = Dataset(test_v, test_t)
loaders = (
    gen_loader(train_dataset, 1, shuffle = True),
    gen_loader(valid_dataset, 1),
)

Préparez une tâche pour calculer la perte et un formateur pour activer l'optimisation.

code

import torch.optim as optim

code

class Task:
    def __init__(self):
        self.criterion = nn.CrossEntropyLoss()
    
    def train_step(self, model, batch):
        model.zero_grad()
        loss = self.criterion(model(batch['x']), batch['t'])
        loss.backward()
        return loss.item()
    
    def valid_step(self, model, batch):
        with torch.no_grad():
            loss = self.criterion(model(batch['x']), batch['t'])
        return loss.item()

code

class Trainer:
    def __init__(self, model, loaders, task, optimizer, max_iter, device = None):
        self.model = model
        self.model.to(device)
        self.train_loader, self.valid_loader = loaders
        self.task = task
        self.max_iter = max_iter
        self.optimizer = optimizer
        self.device = device
    
    def send(self, batch):
        for key in batch:
            batch[key] = batch[key].to(self.device)
        return batch
        
    def train_epoch(self):
        self.model.train()
        acc = 0
        for n, batch in enumerate(self.train_loader):
            batch = self.send(batch)
            acc += self.task.train_step(self.model, batch)
            self.optimizer.step()
        return acc / n
            
    def valid_epoch(self):
        self.model.eval()
        acc = 0
        for n, batch in enumerate(self.valid_loader):
            batch = self.send(batch)
            acc += self.task.valid_step(self.model, batch)
        return acc / n
    
    def train(self):
        for epoch in range(self.max_iter):
            train_loss = self.train_epoch()
            valid_loss = self.valid_epoch()
            print('epoch {}, train_loss:{:.5f}, valid_loss:{:.5f}'.format(epoch, train_loss, valid_loss))

Effectuer l'apprentissage.

code

model = Perceptron(300, 4)
task = Task()
optimizer = optim.SGD(model.parameters(), 0.1)
trainer = Trainer(model, loaders, task, optimizer, 10)
trainer.train()

production

epoch 0, train_loss:0.40178, valid_loss:0.32123
epoch 1, train_loss:0.29685, valid_loss:0.30087
epoch 2, train_loss:0.27381, valid_loss:0.31221
epoch 3, train_loss:0.26309, valid_loss:0.29472
epoch 4, train_loss:0.25435, valid_loss:0.29926
epoch 5, train_loss:0.24851, valid_loss:0.30723
epoch 6, train_loss:0.24424, valid_loss:0.30154
epoch 7, train_loss:0.23987, valid_loss:0.30601
epoch 8, train_loss:0.23762, valid_loss:0.30835
epoch 9, train_loss:0.23378, valid_loss:0.31116

Vous pouvez voir que la perte de données d'entraînement a diminué.

74. Mesure du taux de réponse correcte

Lors de la classification des cas de données d'entraînement et de données d'évaluation à l'aide de la matrice obtenue à la question 73, trouvez le taux de réponse correct pour chacun.

code

import numpy as np

code

class Predictor:
    def __init__(self, model, loader):
        self.model = model
        self.loader = loader
        
    def infer(self, batch):
        self.model.eval()
        return self.model(batch['x']).argmax(dim=-1).item()
        
    def predict(self):
        lst = []
        for batch in self.loader:
            lst.append(self.infer(batch))
        return lst

code

def accuracy(true, pred):
    return np.mean([t == p for t, p in zip(true, pred)])

code

predictor = Predictor(model, Loader(train_dataset, 1))
pred = predictor.predict()
print('Taux de réponse correct dans les données d'entraînement:', accuracy(train_t, pred))

production

Taux de réponse correct dans les données d'entraînement: 0.9239049045301385

code

predictor = Predictor(model, gen_loader(train_dataset, 1))
pred = predictor.predict()
print('Taux de réponse correct dans les données d'entraînement:', accuracy(train_t, pred))

production

Taux de réponse correct dans les données d'évaluation: 0.8952095808383234

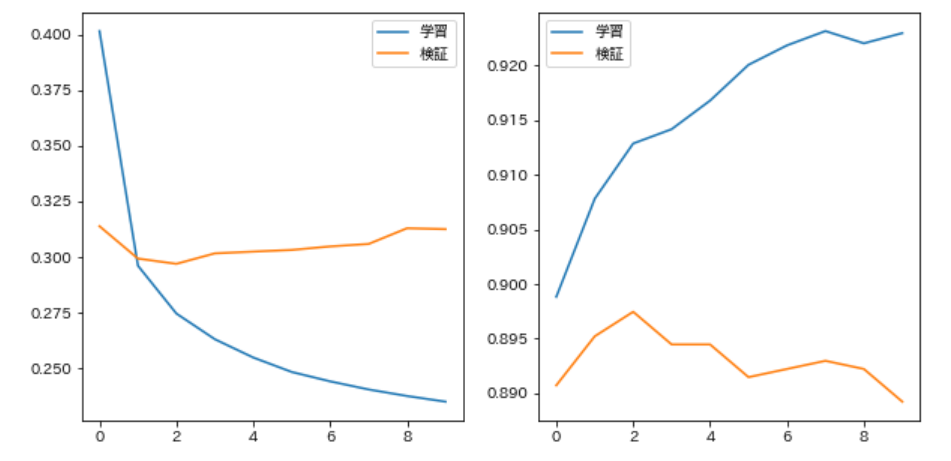
75. Graphique des taux de perte et de précision

En modifiant le code dans Q73, chaque fois que la mise à jour des paramètres de chaque époque est terminée, la perte de données d'apprentissage, le taux de réponse correct, la perte de données de développement et le taux de réponse correct peuvent être tracés sur un graphique pour vérifier la progression de l'apprentissage. Fais le.

code

import matplotlib.pyplot as plt
import japanize_matplotlib
from IPython.display import clear_output

C'est un code qui met à jour la figure en temps réel sur le notebook jupyter.

code

class RealTimePlot:
    def __init__(self, legends):
        self.legends = legends
        self.fig, self.axs = plt.subplots(1, len(legends), figsize = (10, 5))
        self.lst = [[[] for _ in xs] for xs in legends]
        
    def __enter__(self):
        return self
        
    def update(self, *args):
        for i, ys in enumerate(args):
            for j, y in enumerate(ys):
                self.lst[i][j].append(y)
        clear_output(wait = True)
        for i, ax in enumerate(self.axs):
            ax.cla()
            for ys in self.lst[i]:
                ax.plot(ys)
            ax.legend(self.legends[i])
        display(self.fig)
        
    def __exit__(self, *exc_info):
        plt.close(self.fig)

code

class VerboseTrainer(Trainer):
    def accuracy(self, true, pred):
        return np.mean([t == p for t, p in zip(true, pred)])
    
    def train(self, train_v, train_t, valid_v, valid_t):
        train_loader = gen_loader(Dataset(train_v, train_t), 1)
        valid_loader = gen_loader(Dataset(valid_v, valid_t), 1)
        with RealTimePlot([['Apprentissage', 'Vérification']] * 2) as rtp:
            for epoch in range(self.max_iter):
                self.model.to(self.device)
                train_loss = self.train_epoch()
                valid_loss = self.valid_epoch()
                train_acc = self.accuracy(train_t, Predictor(self.model.cpu(), train_loader).predict())
                valid_acc = self.accuracy(valid_t, Predictor(self.model.cpu(), valid_loader).predict())
                rtp.update([train_loss, valid_loss], [train_acc, valid_acc])

Calculez le taux de réponse correct dans le formateur et répétez l'effacement et l'affichage sur le bloc-notes Jupyter.

code

model = Perceptron(300, 4)
task = Task()
optimizer = optim.SGD(model.parameters(), 0.1)
trainer = VerboseTrainer(model, loaders, task, optimizer, 10)
train_predictor = Predictor(model, gen_loader(test_dataset, 1))
valid_predictor = Predictor(model, gen_loader(test_dataset, 1))
trainer.train(train_v, train_t, valid_v, valid_t)

76. Point de contrôle

Modifier le code en question 75 et écrire les points de contrôle (valeurs des paramètres en cours d'apprentissage (matrice de poids, etc.) et état interne de l'algorithme d'optimisation) dans un fichier à chaque fois que la mise à jour des paramètres de chaque époque est terminée.

code

import os

code

class LoggingTrainer(Trainer):
    def save(self, epoch):
        torch.save({'epoch' : epoch, 'optimizer': self.optimizer}, f'trainer_states{epoch}.pt')
        torch.save(self.model.state_dict(), f'checkpoint{epoch}.pt')
    
    def train(self):
        for epoch in range(self.max_iter):
            train_loss = self.train_epoch()
            valid_loss = self.valid_epoch()
            self.save(epoch)
            print('epoch {}, train_loss:{:.5f}, valid_loss:{:.5f}'.format(epoch, train_loss, valid_loss))

Pour sauvegarder le modèle, le dictionnaire de valeurs appelé par state_dict () est aussi torch.save.

code

model = Perceptron(300, 4)
task = Task()
optimizer = optim.SGD(model.parameters(), 0.1)
trainer = LoggingTrainer(model, loaders, task, optimizer, 10)
trainer.train()

production

epoch 0, train_loss:0.40303, valid_loss:0.31214
epoch 1, train_loss:0.29639, valid_loss:0.29592
epoch 2, train_loss:0.27451, valid_loss:0.29903
epoch 3, train_loss:0.26194, valid_loss:0.29984
epoch 4, train_loss:0.25443, valid_loss:0.29787
epoch 5, train_loss:0.24855, valid_loss:0.30021
epoch 6, train_loss:0.24384, valid_loss:0.30676
epoch 7, train_loss:0.24003, valid_loss:0.30658
epoch 8, train_loss:0.23756, valid_loss:0.30995
epoch 9, train_loss:0.23390, valid_loss:0.30879

code

ls result/checkpoint*

production

result/checkpoint0.pt  result/checkpoint4.pt  result/checkpoint8.pt
result/checkpoint1.pt  result/checkpoint5.pt  result/checkpoint9.pt
result/checkpoint2.pt  result/checkpoint6.pt
result/checkpoint3.pt  result/checkpoint7.pt

code

ls result/trainer_states*

production

result/trainer_states0.pt  result/trainer_states4.pt  result/trainer_states8.pt
result/trainer_states1.pt  result/trainer_states5.pt  result/trainer_states9.pt
result/trainer_states2.pt  result/trainer_states6.pt
result/trainer_states3.pt  result/trainer_states7.pt

77. Mini lot

Modifiez le code du problème 76, calculez la perte / gradient pour chaque cas $ B $, et mettez à jour la valeur de la matrice $ W $ (mini-batch). Comparez le temps nécessaire pour apprendre une époque en changeant la valeur de $ B $ en $ 1, 2, 4, 8, \ dots $.

Le mini-lot est déjà implémenté dans Dataset, il suffit donc de changer la largeur de Sampler.

code

from time import time
from contextlib import contextmanager

code

@contextmanager
def timer(description):
    start = time()
    yield
    print(description, ': {:.3f}Secondes'.format(time()-start))

code

B = [1, 2, 4, 8, 16, 32, 64, 128, 256, 512, 1024]

code

task = Task()
for b in B:
    model = Perceptron(300, 4)
    loaders = (
        gen_loader(train_dataset, b, shuffle = True),
        gen_loader(valid_dataset, 1)
    )
    optimizer = optim.SGD(model.parameters(), 0.1 * b)
    trainer = Trainer(model, loaders, task, optimizer, 3)
    with timer(f'Taille du lot{b}'):
        trainer.train()

production

epoch 0, train_loss:0.40374, valid_loss:0.31423
epoch 1, train_loss:0.29578, valid_loss:0.29623
epoch 2, train_loss:0.27499, valid_loss:0.29798
Taille du lot 1: 9.657 secondes
epoch 0, train_loss:0.39955, valid_loss:0.31440
epoch 1, train_loss:0.29591, valid_loss:0.29844
epoch 2, train_loss:0.27373, valid_loss:0.29537
Taille du lot 2: 5.325 secondes
epoch 0, train_loss:0.40296, valid_loss:0.31603
epoch 1, train_loss:0.29613, valid_loss:0.31031
epoch 2, train_loss:0.27469, valid_loss:0.29736
Taille du lot 4: 3.083 secondes
epoch 0, train_loss:0.40289, valid_loss:0.31443
epoch 1, train_loss:0.29676, valid_loss:0.30920
epoch 2, train_loss:0.27498, valid_loss:0.30645
Taille du lot 8: 1.982 secondes
epoch 0, train_loss:0.40211, valid_loss:0.31350
epoch 1, train_loss:0.29613, valid_loss:0.30777
epoch 2, train_loss:0.27449, valid_loss:0.29903
Taille du lot 16: 1.420 secondes
epoch 0, train_loss:0.40343, valid_loss:0.32170
epoch 1, train_loss:0.29695, valid_loss:0.30777
epoch 2, train_loss:0.27486, valid_loss:0.29472
Taille du lot 32: 1.202 secondes
epoch 0, train_loss:0.40753, valid_loss:0.32378
epoch 1, train_loss:0.29829, valid_loss:0.29770
epoch 2, train_loss:0.27663, valid_loss:0.30175
Taille du lot 64: 1.060 secondes
epoch 0, train_loss:0.41799, valid_loss:0.33559
epoch 1, train_loss:0.30109, valid_loss:0.30401
epoch 2, train_loss:0.27763, valid_loss:0.30351
Taille du lot 128: 0.906 secondes
epoch 0, train_loss:0.56407, valid_loss:0.30955
epoch 1, train_loss:0.31099, valid_loss:0.32111
epoch 2, train_loss:0.28797, valid_loss:0.29928
Taille du lot 256: 2.234 secondes
epoch 0, train_loss:1.19123, valid_loss:0.32315
epoch 1, train_loss:0.52350, valid_loss:0.39943
epoch 2, train_loss:0.42246, valid_loss:0.36194
Taille du lot 512: 1.323 secondes
epoch 0, train_loss:3.77615, valid_loss:0.60957
epoch 1, train_loss:1.05934, valid_loss:0.89198
epoch 2, train_loss:0.80346, valid_loss:0.61814
Taille du lot 1024: 1.057 secondes

78. Apprentissage sur GPU

Modifiez le code en question 77 et exécutez la formation sur le GPU.

Si vous le mettez sur torch.device ('cuda'), vous pouvez continuer.

code

device = torch.device('cuda')
model = Perceptron(300, 4)
task = Task()
loaders = (
    gen_loader(train_dataset, 128, shuffle = True),
    gen_loader(valid_dataset, 1),
)
optimizer = optim.SGD(model.parameters(), 0.1 * 128)
trainer = Trainer(model, loaders, task, optimizer, 3, device=device)
with timer('temps'):
    trainer.train()

production

epoch 0, train_loss:0.41928, valid_loss:0.31376
epoch 1, train_loss:0.30053, valid_loss:0.29341
epoch 2, train_loss:0.27865, valid_loss:0.29917
temps: 1.433 secondes

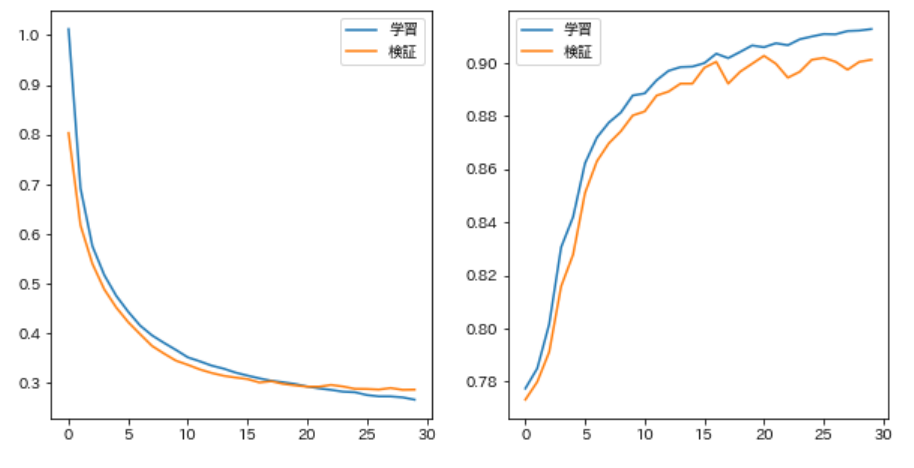
79. Réseau neuronal multicouche

Construisez un classificateur de catégorie haute performance en modifiant le code du problème 78 et en changeant la forme du réseau neuronal, comme l'introduction de termes de biais et de multicouches.

J'ai essayé de le rendre multicouche, mais il semble que les performances ne s'améliorent pas de manière significative par elles-mêmes.

code

class ModelNLP79(nn.Module):
    def __init__(self, v_size, h_size, c_size):
        super().__init__()
        self.fc1 = nn.Linear(v_size, h_size)
        self.act = nn.ReLU()
        self.fc2 = nn.Linear(h_size, c_size)
        self.dropout = nn.Dropout(0.2)
        nn.init.kaiming_normal_(self.fc1.weight)
        nn.init.kaiming_normal_(self.fc2.weight)
        
    def forward(self, x):
        x = self.fc1(x)
        x = self.act(x)
        x = self.dropout(x)
        x = self.fc2(x)
        return x

code

model = ModelNLP79(300, 128, 4)
task = Task()
loaders = (
    gen_loader(train_dataset, 128, shuffle = True),
    gen_loader(valid_dataset, 1)
)
optimizer = optim.SGD(model.parameters(), 0.1)
trainer = VerboseTrainer(model, loaders, task, optimizer, 30, device)
trainer.train(train_v, train_t, valid_v, valid_t)

Vient ensuite le chapitre 9

100 Language Processing Knock 2020 Chapitre 9: RNN, CNN