Profitez deux fois du matériel Coursera / Machine Learning

Dernièrement, je prends le Maechine Learning de Coursera (Stanford University, par Andrew Ng). Bien sûr, la vidéo d'explication est également utile, mais ce qui rend ce cours si bon est la tâche de programmation qui est présentée à chaque fois. C'est juste du code Matlab, donc je voulais le réécrire en Python afin de pouvoir le revoir plus tard. (D'autres personnes peuvent voir des exemples des mêmes efforts sur Internet.)

Ici, je vais vous présenter comment profiter du matériel pédagogique de "Coursera / Machine Learning" deux ou trois fois (en Python). Nous expliquons également ** scipy.optimize.minimize () ** utilisé pour la minimisation des fonctions.

Fonction de coût et son dérivé

De nombreux supports d'apprentissage automatique créent une fonction de coût et recherchent des paramètres qui la minimisent. Matlab utilise fminunc () (ou fmincg () fourni dans la tâche), mais en Python ** scipy.optimize.minimize () ** prend en charge une fonction similaire.

Tout d'abord, préparez vous-même la fonction de coût et son dérivé. Dans la première tâche, le modèle linéaire, il est donné par l'équation suivante.

J(\theta) = \frac{1}{2m} \sum_{i=1}^{m} (h_{\theta}(x ^{(i)} ) -y ^{(i)}) ^2
\\
\frac{\partial J}{\partial \theta _j} = \frac{1}{m} \sum_{i=1}^{m} 
(h_{\theta} (x^{(i)}) - y^{(i)} )x_j^{(i)}

$ h_ {\ theta} $ est la fonction assumée dans la modélisation. (Cette fois, un modèle linéaire est supposé.)

def compute_cost(theta, xmat, ymat):
    m = len(ymat)
    
    one_v = np.ones(len(xmat))
    xmat1 = np.column_stack((one_v, xmat)) # shape: m x 2
    ymat1 = ymat.reshape(len(ymat),1)      # shape: [m,] --> [m,1]
    theta1 = theta.reshape(len(theta),1)
    hx2y = np.dot(xmat1, theta1) - ymat1    # shape: m x 1
    j =  1. /2. /m * np.dot(hx2y.T, hx2y)  # shape: 1 x 1
    
    return j
	
def compute_grad(theta, xmat, ymat):
    j_grad = np.zeros(len(theta), dtype=float)

    m = len(ymat)
    one_v = np.ones(len(xmat))
    xmat1 = np.column_stack((one_v, xmat))
    ymat1 = ymat.reshape(m,1)      # shape: [m,] --> [m,1]
    theta1 = theta.reshape(len(theta),1)
    hx2y = np.dot(xmat1, theta1) - ymat1
    j_grad = 1. /m * np.dot(xmat1.T, hx2y)
    j_grad = j_grad.flatten()      
    
    return j_grad

C'est une implémentation d'une telle fonction. En utilisant ces deux fonctions comme fonctions subordonnées, la recherche de paramètre (thêta) qui minimise le coût est effectuée par la méthode de descente de gradient (Gradient Descent). Tout d'abord, la formule suivante affichée dans Coursera est codée telle quelle et le calcul est effectué.

Formule de descente de gradient:

\theta_i := \theta_j - \alpha \frac{1}{m} \sum_{i=1}^{m} (h_{\theta} (x^{(i)}) - y^{(i)}) x_{j}^{(i)}  \ \ \ \ \ (simultaneously\  update\  \theta_j\  for\  all\  j)

def gradient_descent(theta, alpha, num_iters):
    global xmat, ymat

    m = len(ymat)      # number of train examples
    j_history = np.zeros(num_iters)
    #
    for iter in range(num_iters):
        xmat1 = xmat ; ymat1 = ymat
        delta_t = alpha * compute_grad(theta, xmat1, ymat1)
        theta = theta - delta_t
        # for DEBUG #     
        j_history[iter] = compute_cost(theta, xmat, ymat)

    return theta, j_history

La méthode de descente de gradient la plus simple est celle décrite ci-dessus. Coursera / Machine Learning Ce n'est pas un problème pour la première tâche. La ligne de montage trouvée est la suivante.

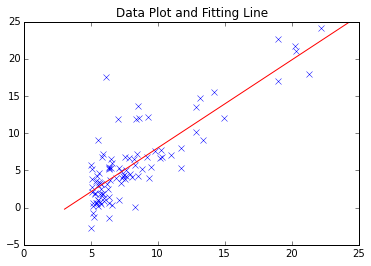
Cependant, compte tenu de la convergence des données à plus grande échelle et de l'analyse de données complexes et de la réponse aux points minimum locaux, il peut y avoir des cas où il peut être tentant d'utiliser un module éprouvé.

Essayez d'utiliser scipy.optimize.minimize ()

Diverses fonctions sont implémentées dans Scipy pour l'optimisation.

http://docs.scipy.org/doc/scipy/reference/optimize.html

Cette fois, j'ai décidé d'utiliser ** scipy.optimize.minimize () **, qui a pour fonction de "minimiser la fonction qui fait référence au paramètre". Extrait de la documentation.

scipy.optimize.minimize (fun, x0, args=(), method=None, jac=None, hess=None, hessp=None, bounds=None, constraints=(), tol=None, callback=None, options=None)

parameters

• fun : callable Objective function.
• x0 : ndarray Initial guess.
• args : tuple, optional Extra arguments passed to the objective function and its derivatives (Jacobian, Hessian).
• method : str or callable, optional Type of solver. Should be one of -- ‘Nelder-Mead’ -- ‘Powell’ -- ‘CG’ -- ‘BFGS’ -- ‘Newton-CG’ -- ‘L-BFGS-B’ -- ‘TNC’ -- ‘COBYLA’ -- ‘SLSQP’ -- ‘dogleg’ -- ‘trust-ncg’ -- custom - a callable object If not given, chosen to be one of BFGS, L-BFGS-B, SLSQP
• jac : bool or callable, optional (Ci-après omis)

Il répertorie des méthodes de calcul que je n'ai pas beaucoup vues, et c'est encourageant même si je ne connais pas le contenu. Tout d'abord, je l'ai testé avec une formule simple.

import scipy.optimize as spo
def fun1(x):
	ans = (x[0] - 1.5) ** 2 + (x[1] - 2.5) ** 2
	
	return ans

def fun1_grad(x):
	dx = np.zeros(2)
	dx[0] = 2 * x[0] - 3
	dx[1] = 2 * x[1] - 5
	
	return dx

x_init = np.array([1.0, 1.0])   # initial value

res1 = spo.minimize(fun1, x_init, method='BFGS', jac=fun1_grad, \
            options={'gtol': 1e-6, 'disp': True})

Cela nous donne $ x = [1,5, 2,5] $, ce qui minimise $ f = (x_0 --1,5) ^ 2 + (x_1 --2,5) ^ 2 $. Les tâches de Coursera sont les suivantes. Tout d'abord, préparez un wrapper pour la fonction de coût et le dérivé.

def compute_cost_sp(theta):
    global xmat, ymat
    j = compute_cost(theta, xmat, ymat)
    
    return j

def compute_grad_sp(theta):
    global xmat, ymat
    j_grad = compute_grad(theta, xmat, ymat)
    
    return j_grad

Le but de ceci est de préciser que le paramètre à rechercher en omettant les arguments (xmat, ymat) est "theta". Appelez scipy.optimize.minimize () en passant une fonction ou un dérivé qui ne prend que "thêta" comme argument. (Je suis censé utiliser des variables globales ...)

    theta_ini = np.zeros(2)
    res1 = spo.minimize(compute_cost_sp, theta_ini, method='BFGS', \
         jac=compute_grad_sp, options={'gtol': 1e-6, 'disp': True})
    print ' theta.processed =', res1.x

En fait, il est possible de passer les données nécessaires (xmat, ymat) avec ** args ** sans écrire de wrapper, mais j'étais conscient de clarifier les "paramètres de réglage" ici. Les résultats du calcul sont les suivants.

#Propre descente de gradient(iteration =2000 fois)
theta =     -3.788,      1.182
# scipy.optimize.minimize()Résultat de
Optimization terminated successfully.
         Current function value: 4.476971
         Iterations: 4
         Function evaluations: 6
         Gradient evaluations: 6
 theta.processed = [-3.89578088  1.19303364]

Essayez d'être stochastique

A partir de là, il s'agit d'une version avancée qui n'est pas incluse dans la tâche (cela a été fait arbitrairement). J'ai essayé un "essai" de Stochastic Gradient Descent, qui est souvent utilisé en Deep Learning.

def stochastic_g_d(theta, alpha, sample_ratio, num_iters):
    # calculate the number of sampling data (original size * sample_ratio)
    sample_num = int(len(ymat) * sample_ratio)

    m = len(ymat)      # number of train examples (total)
    n = np.size(xmat) / len(xmat)
    j_history = np.zeros(num_iters)

    for iter in range(num_iters):
        xs = np.zeros((sample_num, n)) ; ys = np.zeros(sample_num)
 
        for i in range(sample_num):
            myrnd = np.random.randint(m)
            xs[i,:] = xmat[myrnd,]
            ys[i]   = ymat[myrnd]

        delta_t = alpha * compute_grad(theta, xs, ys)
        theta = theta - delta_t
        j_history[iter] = compute_cost(theta, xmat, ymat)
    
    return theta, j_history

Dans le code ci-dessus, le processus de l'échantillonnage à la minimisation des données de train a été effectué par mon propre code, mais bien sûr, il est également possible de trouver la solution avec scipy.optimize.minimize () après avoir échantillonné les données de train.

Pour une explication détaillée de S.G.D. (Stochastic Gradient Descent), reportez-vous à la référence (article Web). Le «cœur» est d'échantillonner les données utilisées pour calculer la fonction de coût et la dérivée. Étant donné que le nombre de données de train cette fois est petit, inférieur à 100, il n'est pas nécessaire d'utiliser S.G.D., mais dans le cas de la gestion de données à grande échelle, l'efficacité du calcul peut être considérablement améliorée.

Ce qui suit est un dessin de la courbe d'apprentissage. (Axe horizontal: nombre de calculs de boucle, axe vertical: coût, méthode de descente de gradient normal et méthode de gradient stochastique.) Gradient Descent Method (reference)

Stochastic Gradient Descent (sampling/whole data= 0.3)

C'est amusant de pouvoir élargir la portée par vous-même tout en effectuant des tâches avec Cousera. Je suis encore en train de suivre le Machine Learning cette fois, mais que dois-je prendre à côté du Machine Learning? Je pense à diverses choses. Récemment, le nombre de cours payants «Spécialisation» est en augmentation, mais certains des cours gratuits sont également intéressants. (Cela prend beaucoup de temps, mais ...)

Les références

• Cousera, Machine Learning (Stanford University) (Un manuel / PDF de la tâche de programmation sera distribué chaque semaine.)
• Scipy Documentation http://docs.scipy.org/doc/scipy/reference/optimize.html
• Theano, Deep Learning Tutorial http://deeplearning.net/tutorial/ --Qiita: [Mise à jour] Expliquez ce qu'est la méthode de descente de gradient stochastique en l'exécutant en Python http://qiita.com/kenmatsu4/items/d282054ddedbd68fecb0 / d282054ddedbd68fecb0)
• (Série) Apprentissage automatique Commençons, méthode de gradient n ° 16 pour l'optimisation http://gihyo.jp/dev/serial/01/machine-learning/0016