google traduit http://scikit-learn.org/0.18/modules/learning_curve.html [scikit-learn 0.18 Guide de l'utilisateur 3. Sélection et évaluation du modèle](http://qiita.com/nazoking@github/items/267f2371757516f8c168#3-%E3%83%A2%E3%83%87%E3%83] À partir de% AB% E3% 81% AE% E9% 81% B8% E6% 8A% 9E% E3% 81% A8% E8% A9% 95% E4% BE% A1)

3.5. Courbe de validation: tracer le score pour évaluer le modèle

Toutes les estimations ont leurs forces et leurs faiblesses. Son erreur de généralisation peut être décomposée en termes de biais, de dispersion et de bruit. L'estimateur ** biais ** est l'erreur moyenne de différents ensembles d'apprentissage. La ** variance ** de l'estimateur indique sa sensibilité au changement d'ensemble d'apprentissage. Le bruit est une caractéristique des données.

Le graphique suivant montre la fonction $ f (x) = \ cos (\ frac {3} {2} \ pi x) $ et un échantillon bruyant de cette fonction. Nous utilisons trois fonctions d'évaluation différentes pour adapter cette fonction: Régression linéaire utilisant des caractéristiques polymorphes du premier ordre, du quatrième ordre et du quinzième ordre. Les estimations initiales sont si simples qu'elles peuvent ne pas correspondre très bien à l'échantillon et à la fonction réelle (biais élevé). Le deuxième estimateur se rapproche presque parfaitement. L'estimateur final se rapproche parfaitement des données d'apprentissage, mais ne correspond pas très bien à la vraie fonction. Autrement dit, il est très sensible aux changements dans les données d'entraînement (forte dispersion).

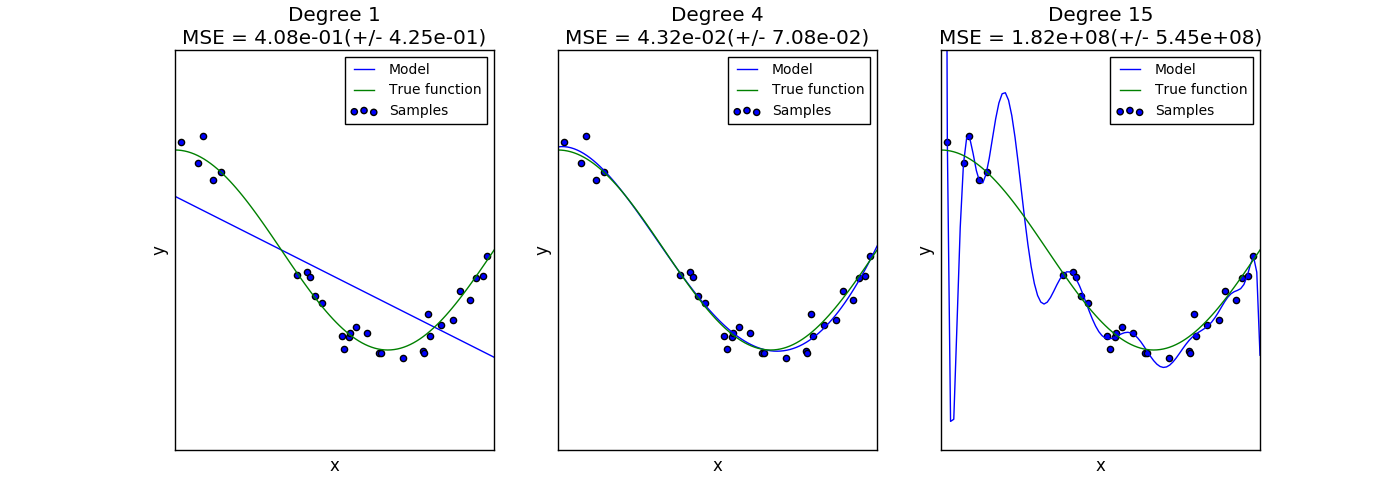
Le biais et la variance sont des propriétés inhérentes aux estimations, et vous devez généralement choisir un algorithme d'apprentissage et des hyperparamètres afin que le biais et la variance soient aussi faibles que possible ([Bias Deviation Dilemma](https: //) Voir en.wikipedia.org/wiki/Bias-variance_dilemma)). Une autre façon de réduire la variance du modèle consiste à utiliser davantage de données d'entraînement. Cependant, si la fonction réelle est trop complexe pour être approximée par un estimateur avec une petite variance, il faut collecter davantage de données d'apprentissage. Avec un simple problème unidimensionnel comme celui que nous avons vu dans cet exemple, il est facile de voir si l'estimateur souffre de biais ou de dispersion. Cependant, dans des espaces dimensionnels plus élevés, il peut être très difficile de visualiser le modèle. Pour cette raison, il peut être utile d'utiliser les outils ci-dessous.

3.5.1. Courbe de vérification

Pour valider le modèle, vous avez besoin d'une fonction de notation (voir Évaluation du modèle: quantifier la qualité des prédictions (http://qiita.com/nazoking@github/items/958426da6448d74279c7)). Par exemple, la précision du classificateur. Pour un bon moyen de sélectionner plusieurs hyperparamètres d'estimateur, voir Grid Search ou une méthode similaire (voir Ajustement des hyperparamètres d'estimation (http://qiita.com/nazoking@github/items/09a4c63614797a6bd705). ), Et sélectionnez l'hyperparamètre avec le score le plus élevé dans l'ensemble de validation ou dans plusieurs ensembles de validation. Notez que si vous optimisez vos hyperparamètres en fonction de votre score de validation, votre score de validation sera biaisé et ne constituera plus une bonne estimation de généralisation. Pour obtenir une bonne évaluation de la généralisation, vous devez calculer le score dans un ensemble de tests distinct. Cependant, il peut être utile de tracer les effets d'un hyperparamètre sur les scores d'entraînement et de validation pour voir si les estimations correspondent trop bien ou sont inadéquates pour certaines valeurs d'hyperparamètres. Dans ce cas, en utilisant la fonction validation_curve:

>>> import numpy as np
>>> from sklearn.model_selection import validation_curve
>>> from sklearn.datasets import load_iris
>>> from sklearn.linear_model import Ridge

>>> np.random.seed(0)
>>> iris = load_iris()
>>> X, y = iris.data, iris.target
>>> indices = np.arange(y.shape[0])
>>> np.random.shuffle(indices)
>>> X, y = X[indices], y[indices]

>>> train_scores, valid_scores = validation_curve(Ridge(), X, y, "alpha",
...                                               np.logspace(-7, 3, 3))
>>> train_scores           
array([[ 0.94...,  0.92...,  0.92...],
       [ 0.94...,  0.92...,  0.92...],
       [ 0.47...,  0.45...,  0.42...]])
>>> valid_scores           
array([[ 0.90...,  0.92...,  0.94...],
       [ 0.90...,  0.92...,  0.94...],
       [ 0.44...,  0.39...,  0.45...]])

Si le score d'entraînement et le score de validation sont faibles, l'estimateur est sous-ajusté. Si le score d'entraînement est élevé et le score de validation faible, l'estimateur est surajusté, sinon il fonctionne très bien. Il n'y a généralement pas de scores d'entraînement faibles et de scores de validation élevés. Les trois cas se trouvent dans le graphique ci-dessous, qui modifie le paramètre SVM $ \ gamma $ dans le jeu de données chiffres.

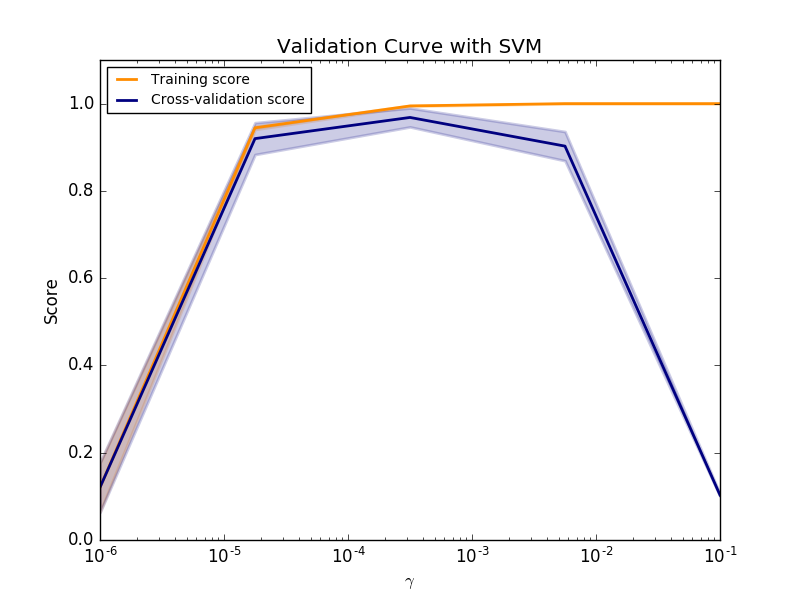
3.5.2. Courbe d'apprentissage

La courbe d'apprentissage montre la validation de l'estimateur et les scores d'entraînement pour différents nombres d'échantillons d'apprentissage. Il s'agit d'un outil pour voir à quel point vous pouvez bénéficier de l'ajout de données d'apprentissage et si l'estimateur souffre encore d'erreurs de dispersion ou de biais. Si le score de validation et le score d'entraînement convergent vers des valeurs trop faibles à mesure que la taille de l'ensemble d'apprentissage augmente, l'augmentation des données d'entraînement ne sera pas bénéfique. Vous pouvez voir un exemple dans le graphique ci-dessous. Les Bayes natifs convergent généralement vers un score faible.

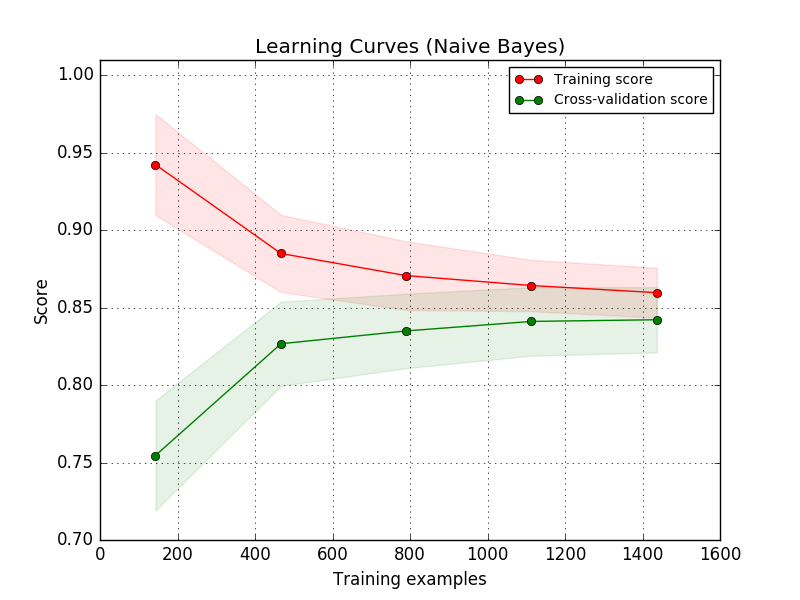
Vous devez peut-être utiliser la paramétrisation d'un estimateur ou d'un estimateur courant qui vous permet d'apprendre des concepts plus complexes (c'est-à-dire moins biaisés). Si le score de formation est beaucoup plus élevé que le score de validation pour le nombre maximum d'échantillons de formation, l'ajout d'échantillons de formation est le plus susceptible d'augmenter la généralisation. Dans le graphique ci-dessous, vous pouvez voir que SVM bénéficie de plus d'exemples de formation.

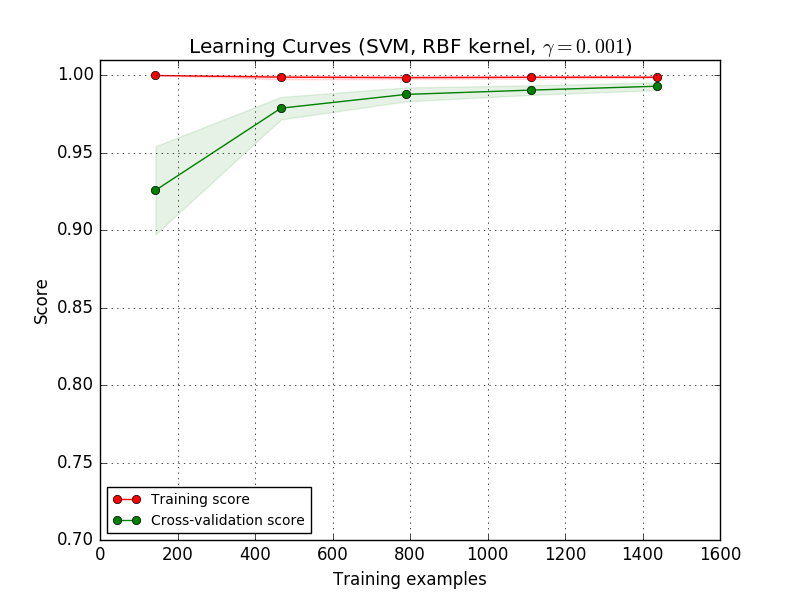
Utilisation de la fonction learning_curve, telle une courbe d'apprentissage (exemple utilisé) Vous pouvez générer les valeurs nécessaires pour tracer le nombre de, le score moyen de l'ensemble d'apprentissage et le score moyen de l'ensemble de validation.

>>> from sklearn.model_selection import learning_curve
>>> from sklearn.svm import SVC

>>> train_sizes, train_scores, valid_scores = learning_curve(
...     SVC(kernel='linear'), X, y, train_sizes=[50, 80, 110], cv=5)
>>> train_sizes            
array([ 50, 80, 110])
>>> train_scores           
array([[ 0.98...,  0.98 ,  0.98...,  0.98...,  0.98...],
       [ 0.98...,  1.   ,  0.98...,  0.98...,  0.98...],
       [ 0.98...,  1.   ,  0.98...,  0.98...,  0.99...]])
>>> valid_scores           
array([[ 1. ,  0.93...,  1. ,  1. ,  0.96...],
       [ 1. ,  0.96...,  1. ,  1. ,  0.96...],
       [ 1. ,  0.96...,  1. ,  1. ,  0.96...]])

[scikit-learn 0.18 Guide de l'utilisateur 3. Sélection et évaluation du modèle](http://qiita.com/nazoking@github/items/267f2371757516f8c168#3-%E3%83%A2%E3%83%87%E3%83] À partir de% AB% E3% 81% AE% E9% 81% B8% E6% 8A% 9E% E3% 81% A8% E8% A9% 95% E4% BE% A1)

[Français] scikit-learn 0.18 Guide de l'utilisateur 3.5. Courbe de vérification: tracez le score pour évaluer le modèle

3.5. Courbe de validation: tracer le score pour évaluer le modèle

3.5.1. Courbe de vérification

3.5.2. Courbe d'apprentissage