[Français] scikit-learn 0.18 Guide de l'utilisateur 2.8. Estimation de la densité

google traduit http://scikit-learn.org/0.18/modules/density.html [scikit-learn 0.18 Guide de l'utilisateur 2. Apprendre sans enseignant](http://qiita.com/nazoking@github/items/267f2371757516f8c168#2-%E6%95%99%E5%B8%AB%E3%81%AA À partir de% E3% 81% 97% E5% AD% A6% E7% BF% 92)

2.8. Estimation de la densité

L'estimation de la densité suit la ligne entre l'apprentissage non supervisé, l'ingénierie des fonctionnalités et la modélisation des données. Certaines des techniques d'estimation de densité les plus courantes et les plus utiles sont le mélange gaussien ([sklearn.mixture.GaussianMixture](http://scikit-learn.org/0.18/modules/generated/sklearn.mixture.GaussianMixture.html#sklearn] .mixture.GaussianMixture)) et estimation de la densité du noyau (sklearn.neighbors.KernelDensity .neighbours.KernelDensity)) est une approche basée sur le voisinage. Le mixage gaussien est décrit plus en détail dans le contexte du clustering (http://scikit-learn.org/0.18/modules/clustering.html#clustering). Cela sert également de schéma de clustering non supervisé. L'estimation de la densité est un concept très simple et la plupart des gens connaissent déjà la méthode populaire d'estimation de la densité, l'histogramme.

2.8.1. Estimation de la densité: histogramme

Un histogramme est une simple visualisation des données dans lesquelles les bacs sont définis, résumant le nombre de points de données dans chaque bac. Un exemple d'histogramme est affiché dans le panneau supérieur gauche de la figure suivante.

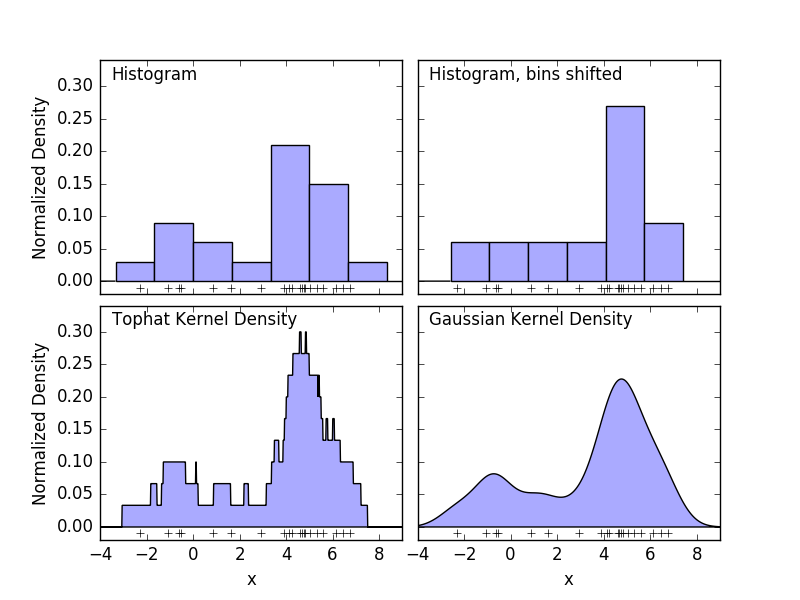
Cependant, le gros problème avec les histogrammes est que les choix de regroupement peuvent avoir un effet disproportionné sur la visualisation résultante. Considérez le panneau supérieur droit dans la figure ci-dessus. Déplacez le bac vers la droite pour voir un histogramme des mêmes données. Les résultats des deux visualisations peuvent sembler très différents et l'interprétation des données peut être différente. Intuitivement, vous pouvez considérer l'histogramme comme une pile de blocs, un bloc par point. Récupérez l'histogramme en empilant des blocs dans l'espace de grille approprié. Mais que se passe-t-il si, au lieu d'empiler des blocs sur une grille régulière, placez chaque bloc au centre du point qu'il représente et additionnez la hauteur totale de chaque position? Cette idée conduit à la visualisation en bas à gauche. Peut-être pas aussi propre qu'un histogramme, mais le fait que les données déterminent la position du bloc signifie qu'il s'agit d'une bien meilleure représentation des données sous-jacentes. Cette visualisation est un exemple d'estimation de la densité du noyau, auquel cas nous utilisons le noyau haut de forme (blocs carrés à chaque point). Vous pouvez restaurer une distribution plus fluide en utilisant un noyau plus fluide. Le graphique en bas à droite montre l'estimation de la densité du noyau gaussien. Ici, chaque point donne une courbe gaussienne à la somme. Le résultat est une estimation de densité lisse dérivée des données, qui agit comme un modèle non paramétrique puissant de la distribution des points.

2.8.2. Estimation de la densité du noyau

L'estimation de la densité du noyau dans scikit-learn est sklearn.neighbors.KernelDensity Il est mis en œuvre. Il utilise un arbre à billes ou un arbre KD pour des requêtes efficaces (voir Nearest Neighbours pour ces discussions). prière de se référer à). L'exemple ci-dessus utilise un ensemble de données 1D pour plus de simplicité, mais l'estimation de la densité du noyau peut être effectuée dans n'importe quel nombre de dimensions. Cependant, en réalité, la malédiction de la dimension réduit les performances à un niveau supérieur.

La figure suivante tire 100 points de la distribution bimodale et fournit des estimations de la densité du noyau pour les trois choix de noyau.

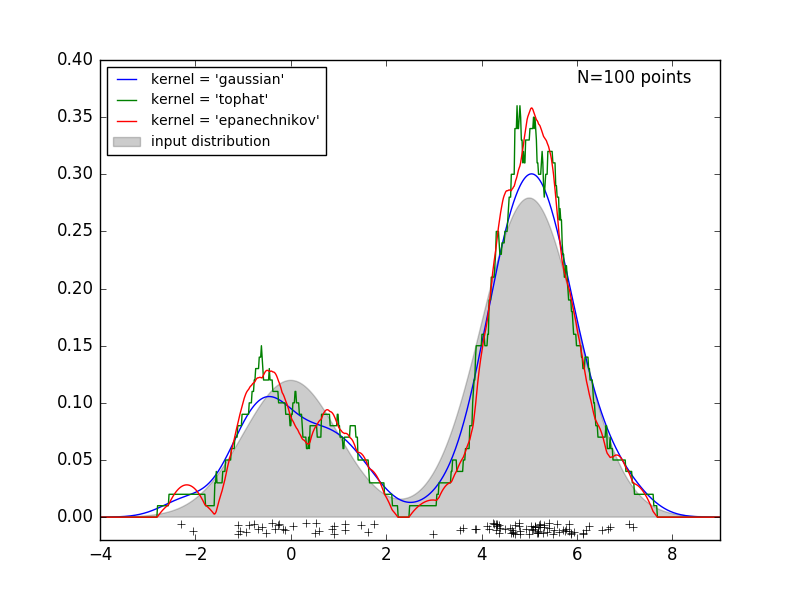
Il est clair comment la forme du noyau affecte la régularité de la distribution résultante. L'estimateur de densité du noyau scikit-learn peut être utilisé comme suit:

>>> from sklearn.neighbors.kde import KernelDensity
>>> import numpy as np
>>> X = np.array([[-1, -1], [-2, -1], [-3, -2], [1, 1], [2, 1], [3, 2]])
>>> kde = KernelDensity(kernel='gaussian', bandwidth=0.2).fit(X)
>>> kde.score_samples(X)
array([-0.41075698, -0.41075698, -0.41076071, -0.41075698, -0.41075698,
       -0.41076071])

Ici, nous utilisons kernel = 'gaussian' comme ci-dessus. Mathématiquement, le noyau est une fonction positive $ K (x; h) $, qui est contrôlée par le paramètre de bande passante $ h $. Étant donné cette forme de noyau, l'estimation de la densité au point y dans le groupe de points N est donnée par:

\rho_K(y) = \sum_{i=1}^{N} K((y - x_i) / h)

La bande passante agit ici comme un paramètre de lissage et contrôle le compromis entre biais et dispersion dans les résultats. Une large bande passante se traduit par une distribution de densité très douce (c'est-à-dire fortement biaisée). Une bande passante étroite entraîne une distribution de densité non uniforme (c'est-à-dire très dispersée). sklearn.neighbors.KernelDensity implémente certains formats de noyau courants. Ceci est illustré dans la figure suivante.

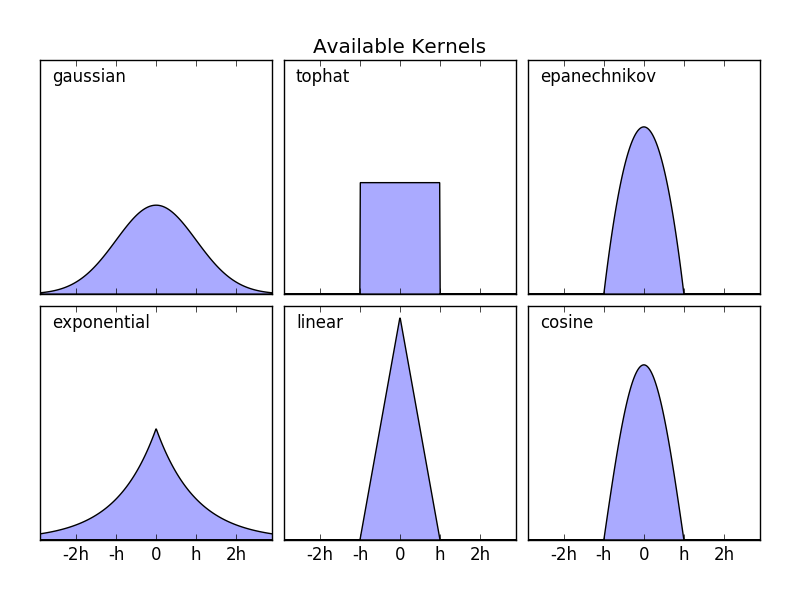
Le format de ces noyaux est:

• Noyau gaussien kernel = 'gaussian'
  • K(x; h) \propto \exp(- \frac{x^2}{2h^2} )
• Noyau Tophat kernel = 'tophat'
  • K(x; h) \propto 1 if x < h
• Noyau Epanechnikov kernel = 'epanechnikov'
  • K(x; h) \propto 1 - \frac{x^2}{h^2}
• Noyau exponentiel kernel = 'exponentiel'
  • K(x; h) \propto \exp(-x/h)
• Noyau linéaire kernel = 'linear'
  • K(x; h) \propto 1 - x/h if x < h
• Noyau cosinus kernel = 'cosinus'
  • K(x; h) \propto \cos(\frac{\pi x}{2h}) if x < h

L'estimation de la densité du noyau est une mesure de distance valide (sklearn.neighbors.DistanceMetric Vous pouvez utiliser n'importe lequel de ceux-ci (voir), mais les résultats ne seront correctement normalisés que pour les métriques euclidiennes. Une métrique particulièrement utile est la distance Haversine (https://en.wikipedia.org/wiki/Haversine_formula), qui mesure la distance angulaire entre les points d'une sphère. L'exemple suivant utilise l'estimation de la densité du noyau pour la visualisation des données géospatiales. Dans cet exemple, la distribution des observations pour deux espèces différentes sur le continent sud-américain:

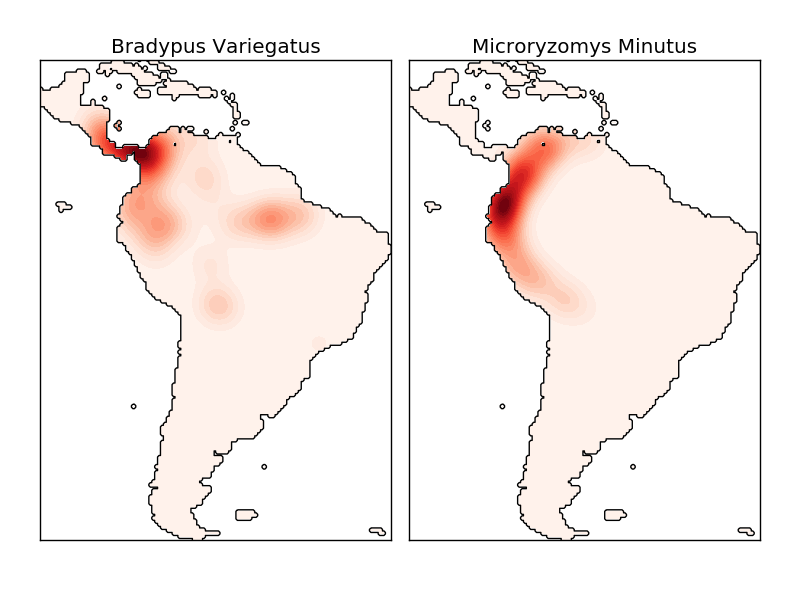
Une autre application utile de l'estimation de la densité du noyau est de former un modèle de génération non paramétrique d'un ensemble de données afin de dériver efficacement de nouveaux échantillons à partir de ce modèle de génération. Voici un exemple d'utilisation de ce processus pour créer un nouvel ensemble de nombres manuscrits à l'aide du noyau gaussien appris dans la projection PCA de données.

Les «nouvelles» données consistent en une combinaison linéaire de données d'entrée et sont dessinées de manière probabiliste en supposant un modèle KDE.

• Exemple:
• Estimation simple de la densité du noyau 1D: 1 Calcul d'estimations simples de la densité du noyau en dimensions.
• Estimation de la densité du noyau: densité de la carte Un exemple d'utilisation de l'estimation pour former un modèle pour générer des données numériques manuscrites et dessiner un nouvel échantillon à partir de ce modèle.
• Estimation de la densité du noyau de la distribution des espèces: Géographie Un exemple d'estimation de la densité du noyau à l'aide de la métrique de distance Haversine pour visualiser des données spatiales

[scikit-learn 0.18 Guide de l'utilisateur 2. Apprendre sans enseignant](http://qiita.com/nazoking@github/items/267f2371757516f8c168#2-%E6%95%99%E5%B8%AB%E3%81%AA À partir de% E3% 81% 97% E5% AD% A6% E7% BF% 92)

© 2010 --2016, développeurs scikit-learn (licence BSD).