We will implement the optimization algorithm (firefly algorithm)
Introduction
A series of optimization algorithm implementations. First, look at Overview.
The code can be found on github.
Firefly algorithm
The Firefly Algorithm is an algorithm that focuses on the courtship behavior of fireflies. Model according to the following rules of conduct.
- Firefly light intensity is an evaluation value
- Other fireflies approach the firefly that emits strong light
- The more attractive you are, the closer other fireflies will come
- Fly randomly when there are no glowing fireflies nearby
- Algorithm flow

- Term correspondence
| problem | Firefly algorithm |
|---|---|
| Array of input values | Firefly position |
| Input value | fire Fly |
| Evaluation value | ホタルの位置におけるEvaluation value(ホタルの光の強さ) |
- Regarding hyperparameters
| Variable name | meaning | Remarks |
|---|---|---|
| attracting_degree | Attracting degree( |
The larger it is, the greater the rate of approaching fireflies |
| absorb | Light absorption coefficient( |
The larger the value, the more light is attenuated.(I can't see the fireflies in the distance) |
| alpha | Random number reflection rate(0.0~1.0) | The larger it is, the better it moves randomly |
| is_normalization | Whether to normalize the Euclidean distance | When normalized, it feels good if the absorb value is around 20-100. |
Firefly movement
The movement of fireflies compares two individuals, and if the light of the other party is stronger, it moves closer. The mobile type is as follows.
| Formula | meaning | Hyperparameters |
|---|---|---|
| Target firefly | ||
| Opponent's firefly | ||
| Coordinate | ||
| Distance between two fireflies(※1) | ||
| Light absorption coefficient(constant) | absorb | |
| Firefly attraction(constant) | attracting_degree | |
| Attractive value of the opponent's firefly | ||
| Times of Day | ||
| Rate of incorporating random elements(constant) | alpha | |
| Random number in the same dimension as the coordinates(※2) |
- 1, implementation is Euclidean distance, but it seems that other distances are also acceptable
- 2, uniform distribution in implementation, but normal distribution seems to be acceptable
import random
import numpy as np
i =Index of my firefly
j =Index of the other party's firefly
#Love Move if the light of other fireflies is strong
if fireflys[i].getScore() < fireflys[j].getScore():
pos = np.asarray(fireflys[i].getArray())
pos2 = np.asarray(fireflys[j].getArray())
d = np.linalg.norm(pos2 - pos) #Euclidean distance
attract = attracting_degree * (math.exp(-absorb * (d ** 2)))
#range+Uniform random number in the range of negative values
r = []
for _ in range(problem.size)
t = random.randint(0, 1)
if t == 0:
t = -1
r.append(problem.randomVal() * t)
r = np.asarray(r)
#Calculate coordinates
pos = pos + attract * (pos2 - pos) + alpha * r
#update
fireflys[i].setArray(pos)
Euclidean distance normalization
$ attract $ is significantly affected by the Euclidean distance value. However, when the number of dimensions changes, the range of the Euclidean distance also changes as follows.
Euclidean distance when separated by 1 in all dimensions 1D: $ \ sqrt {1 ^ 2} = 1 $ 2D: $ \ sqrt {1 ^ 2 + 1 ^ 2} = 1.4142 $ 3D: $ \ sqrt {1 ^ 2 + 1 ^ 2 + 1 ^ 2} = 1.7320 $
Therefore, I normalized it so that it falls within the range of 0 to 1 in any dimension. This normalization process is original to this article and is not in the original algorithm.
import random
import numpy as np
#Maximum n-dimensional distance
t = [problem.MAX_VAL - problem.MIN_VAL for _ in range(problem.size)]
#Maximum euclidean distance
max_norm = np.linalg.norm(t)
#Get the Euclidean distance of i and j fireflies
pos1 = np.asarray(fireflys[i].getArray())
pos2 = np.asarray(fireflys[j].getArray())
d = np.linalg.norm(pos2 - pos)
#Normalize the Euclidean distance in the range 0 to 1
d = d / max_norm
Regarding the attractiveness value of fireflies
It is $ attract $, which is important in the firefly algorithm, but I tried to graph how it changes depending on the value of $ \ gamma $ (absorb). (attracting_degree is 1)

The x-axis is the Euclidean distance to the other firefly, and the y-axis is the attract value. The larger the attract, the closer to the opponent's firefly.
As you can see from the graph, the value of attract decreases sharply after a certain distance.
I felt that normalization was necessary to make this attract value easier to control, so I added an implementation.
Whole code
import math
import random
import numpy as np
class Firefly(IAlgorithm):
def __init__(self,
firefly_max,
attracting_degree=1.0,
absorb=0.5,
alpha=1.0,
is_normalization=False,
):
self.firefly_max = firefly_max
self.attracting_degree = attracting_degree
self.absorb = absorb
self.alpha = alpha
self.is_normalization = is_normalization
def init(self, problem):
self.problem = problem
#For Euclidean distance normalization
t = [problem.MAX_VAL - problem.MIN_VAL for _ in range(problem.size)]
self.max_norm = np.linalg.norm(t)
self.fireflys = []
for _ in range(self.firefly_max):
self.fireflys.append(problem.create())
def step(self):
for i in range(len(self.fireflys)):
for j in range(len(self.fireflys)):
if i == j:
continue
#Move if the light is strong
if self.fireflys[i].getScore() < self.fireflys[j].getScore():
pos = self.fireflys[i].getArray()
pos2 = self.fireflys[j].getArray()
d = np.linalg.norm(pos2 - pos) #Euclidean distance
if self.is_normalization:
#Normalize in the range 0 to 1
d /= self.max_norm
#Attracting degree
attract = self.attracting_degree * (math.exp(-self.absorb * (d ** 2)))
#range+Uniform random number in the range of negative values
r = []
for _ in range(problem.size)
t = random.randint(0, 1)
if t == 0:
t = -1
r.append(problem.randomVal() * t)
r = np.asarray(r)
pos = pos + attract * (pos2 - pos) + self.alpha * r
#update
self.fireflys[i].setArray(pos)
Hyperparameter example
It is the result of optimizing hyperparameters with optuna for each problem. A single optimization attempt yields results with a search time of 2 seconds. I did this 100 times and asked optuna to find the best hyperparameters.
| problem | absorb | alpha | attract | firefly_max | is_normalization |
|---|---|---|---|---|---|
| EightQueen | 30.348200739383188 | 0.023361773591726337 | 0.2870040283132875 | 35 | True |
| function_Ackley | 28.535248274373334 | 0.02020150316119749 | 0.3817578607938779 | 22 | True |
| function_Griewank | 24.886474482157883 | 0.030874057659246265 | 0.2570801290508207 | 16 | True |
| function_Michalewicz | 12.85000382821637 | 0.00019928439251062913 | 0.9311223660128144 | 38 | True |
| function_Rastrigin | 12.146442425313117 | 0.0043715893301495105 | 0.6005897245267422 | 23 | True |
| function_Schwefel | 19.283223050420563 | 0.7687804405285998 | 0.09958914072852465 | 30 | False |
| function_StyblinskiTang | 22.45670196693838 | 0.040041083413524164 | 0.6313203783344563 | 8 | True |
| function_XinSheYang | 19.93462659647029 | 0.7629337202966674 | 0.7449791915452185 | 12 | False |
| g2048 | 15.50932867945044 | 0.8550076810686411 | 0.29794958618177236 | 22 | True |
| LifeGame | 9.681288121919476 | 0.46635850168820797 | 0.9893266181614047 | 42 | True |
| OneMax | 3.0779446144304785 | 0.6083197521965231 | 0.8027617234478412 | 48 | True |
| TSP | 13.999384524084206 | 0.08809615253769626 | 0.46965098629117824 | 21 | True |
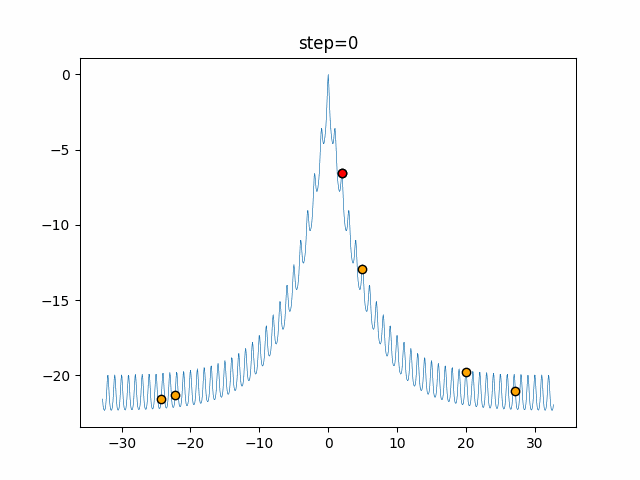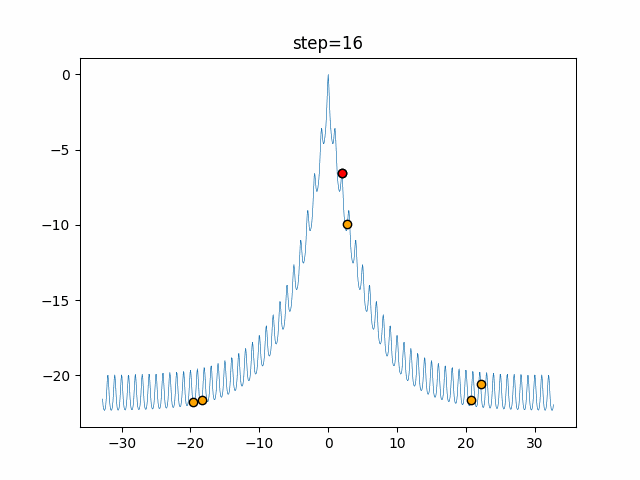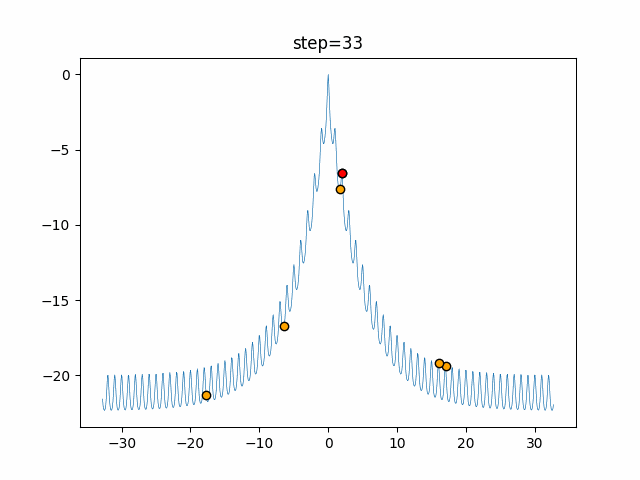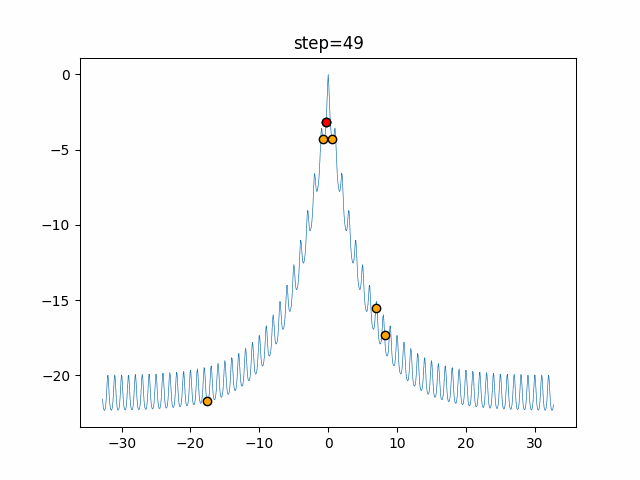
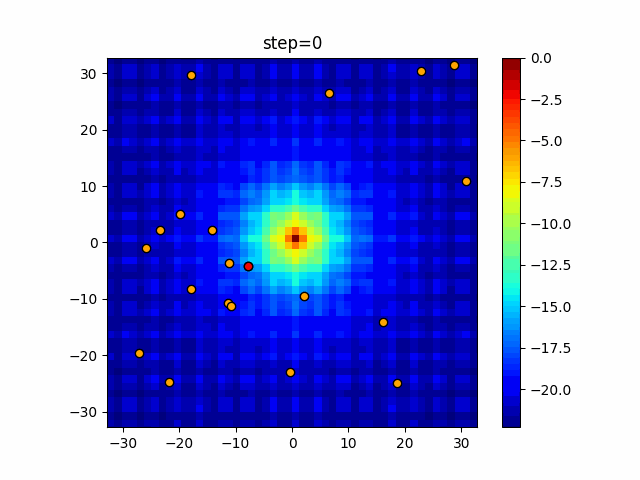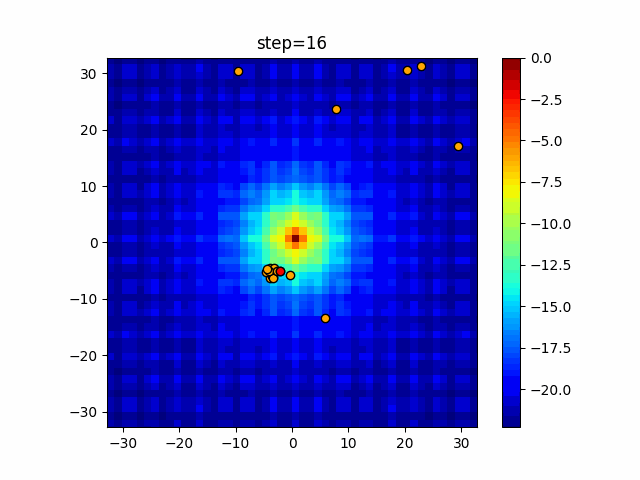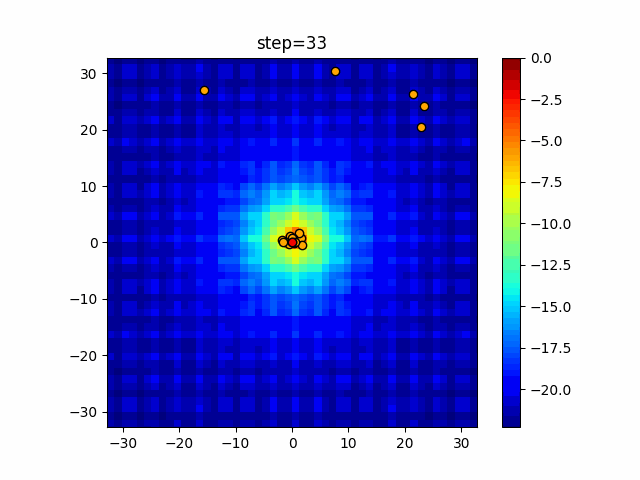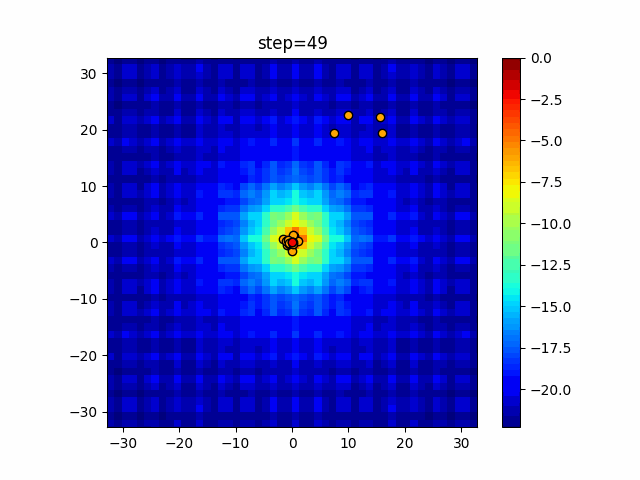
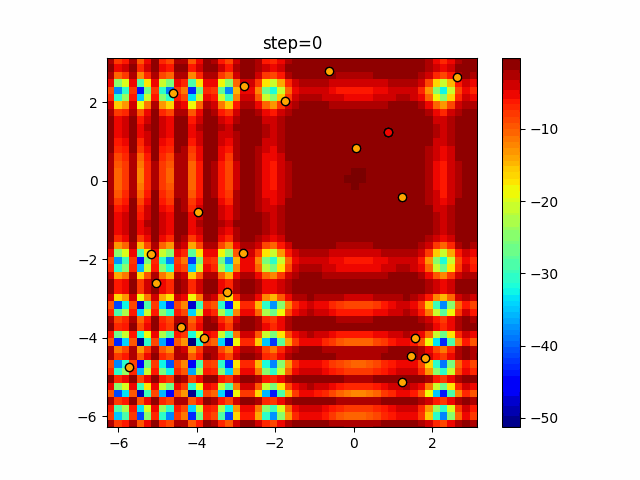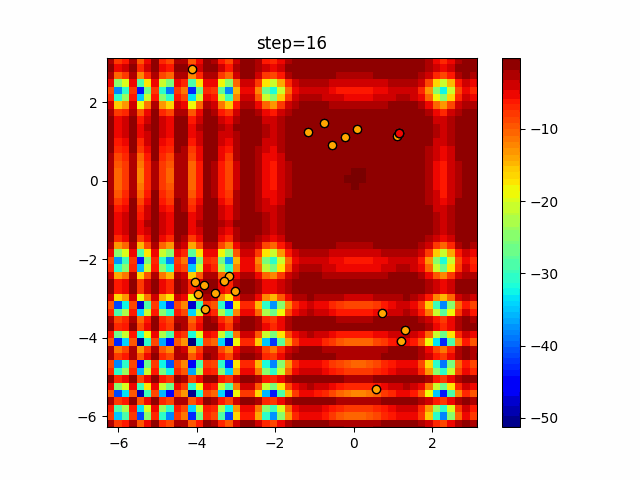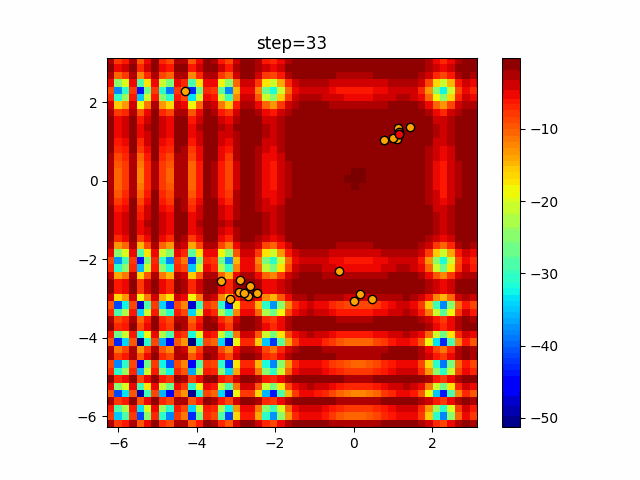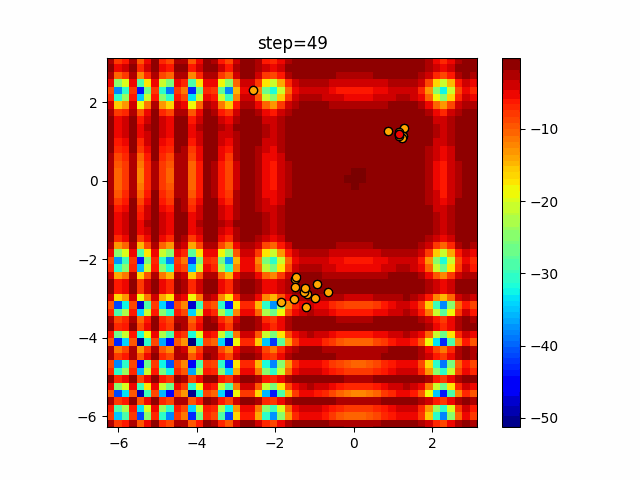
Visualization of actual movement
The 1st dimension is 6 individuals, and the 2nd dimension is 20 individuals, which is the result of 50 steps. The red circle is the individual with the highest score in that step.
The parameters were executed below.
Firefly(N, attracting_degree=0.08, absorb=50.0, alpha=0.03, is_normalization=True)
function_Ackley
- 1D
- 2D
function_Rastrigin
- 1D
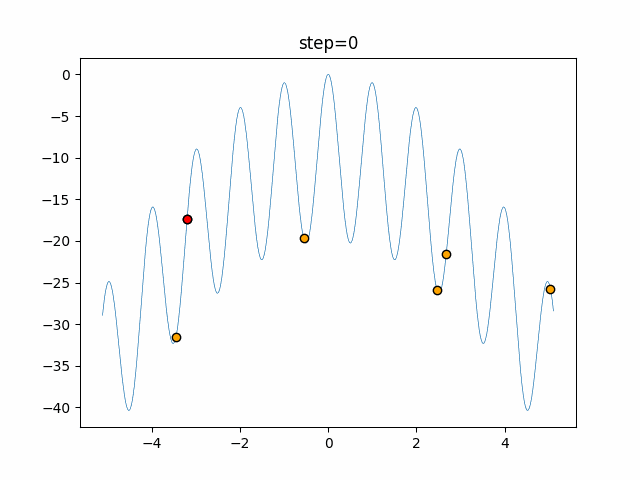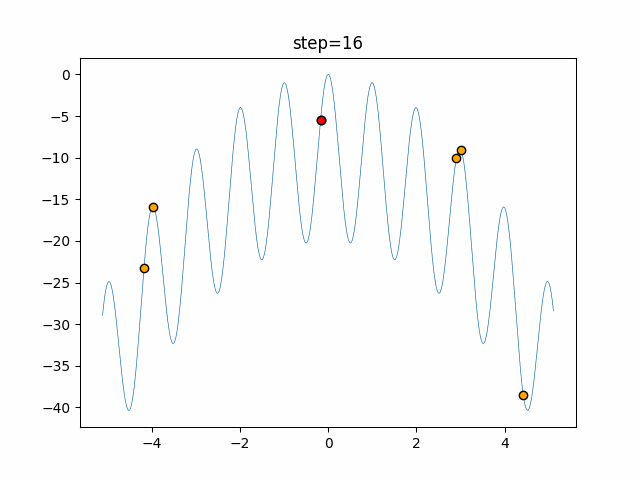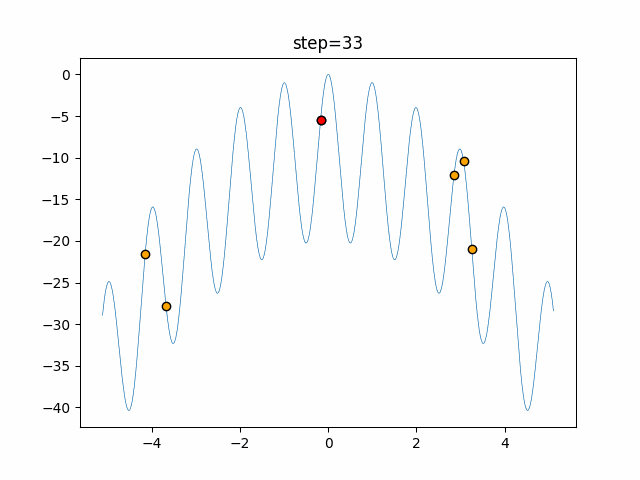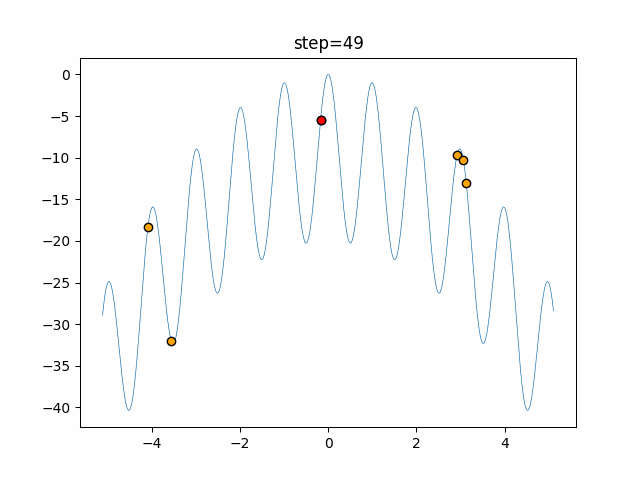
- 2D
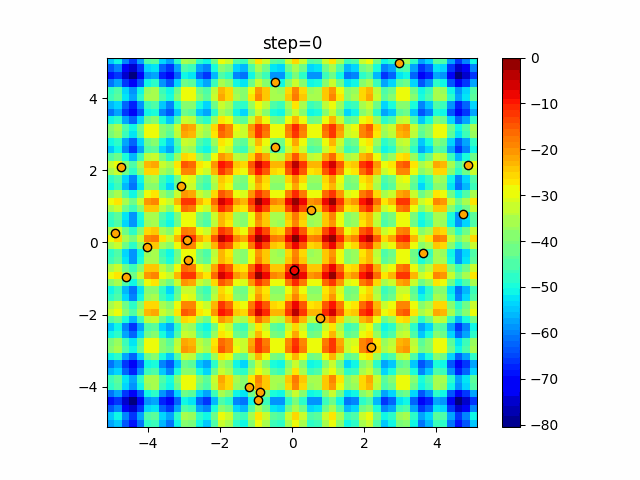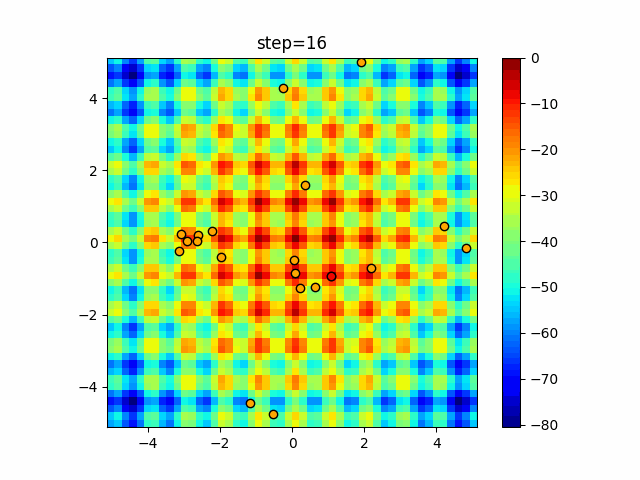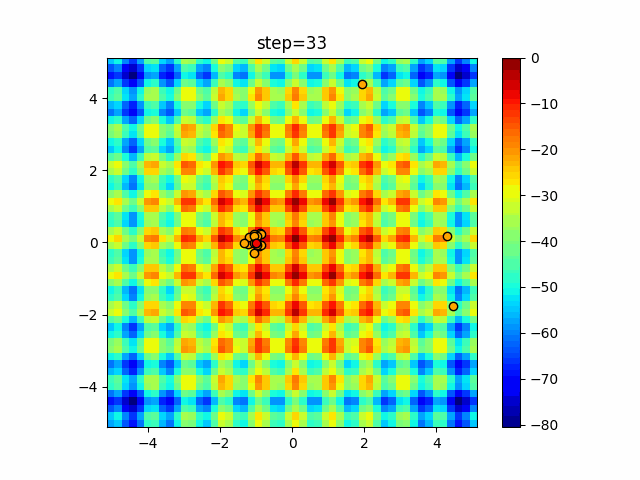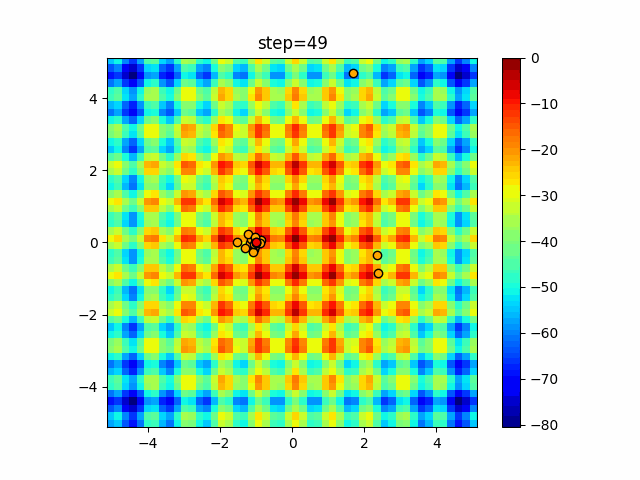
function_Schwefel
- 1D
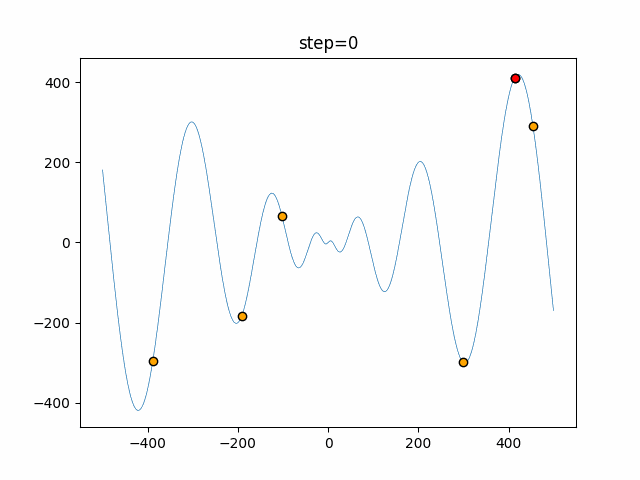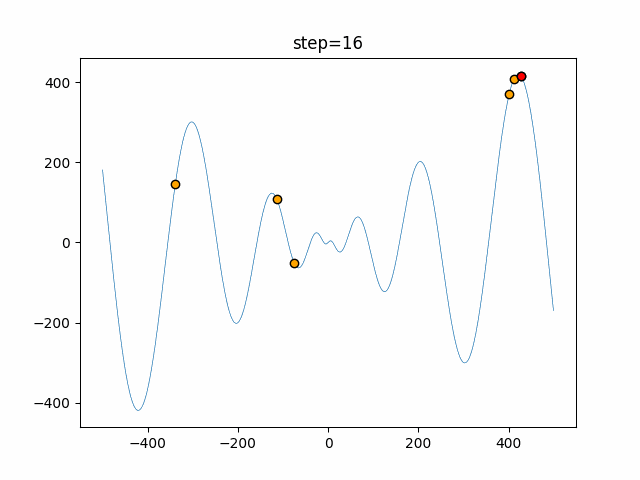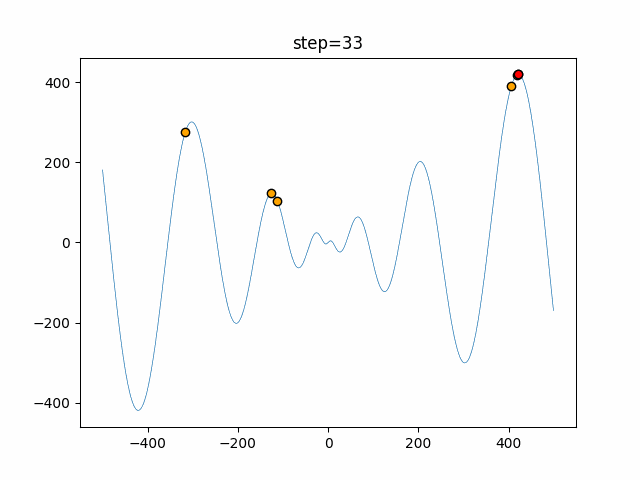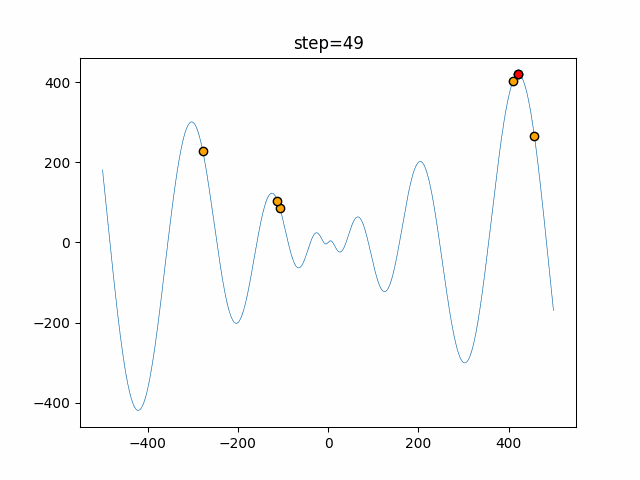
- 2D
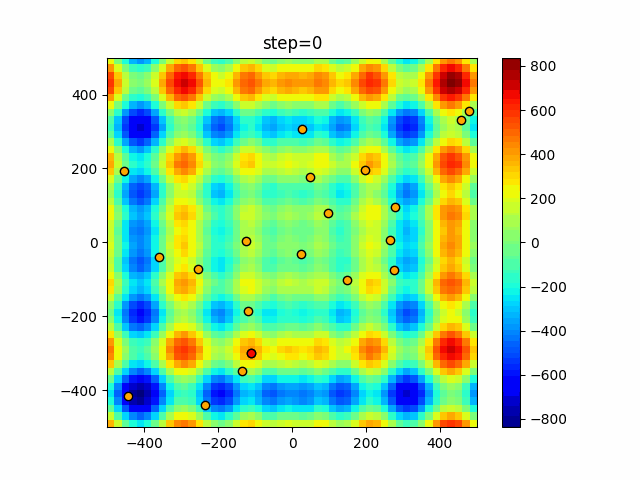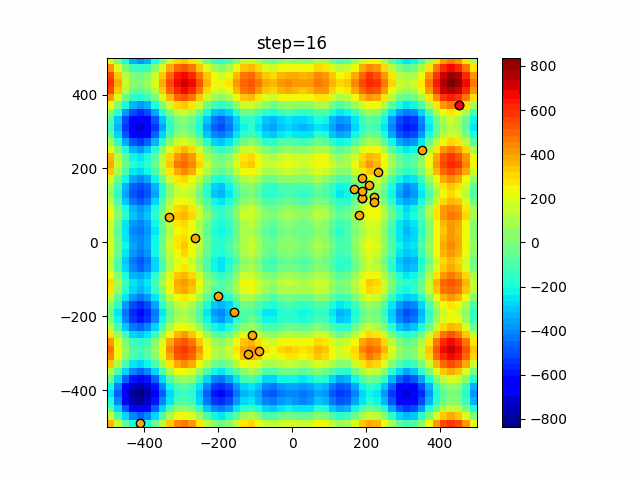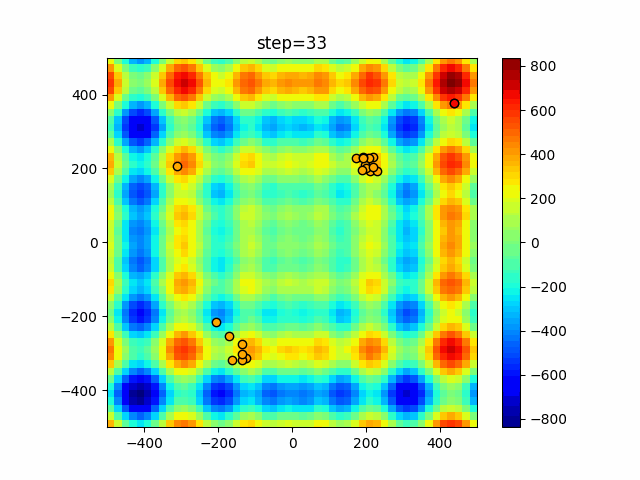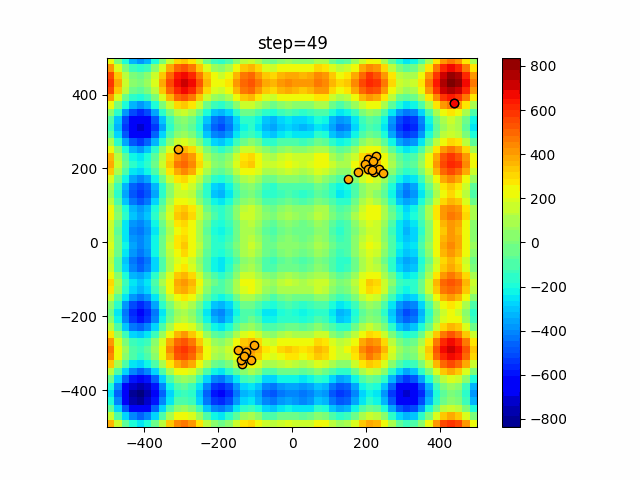
function_StyblinskiTang
- 1D
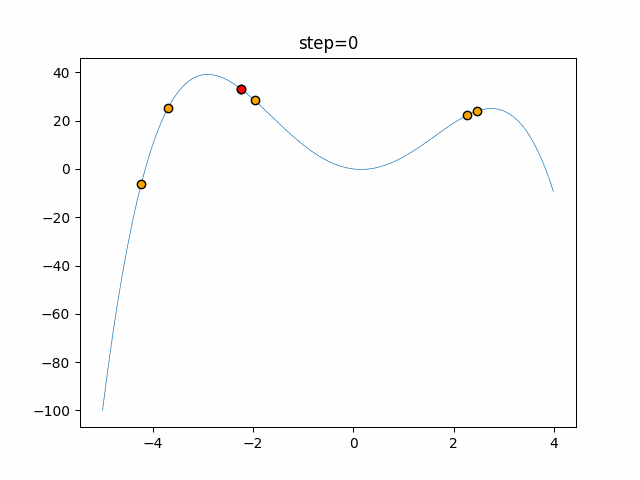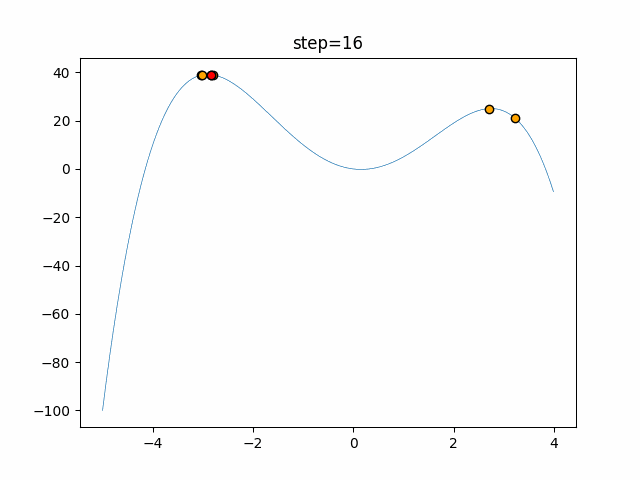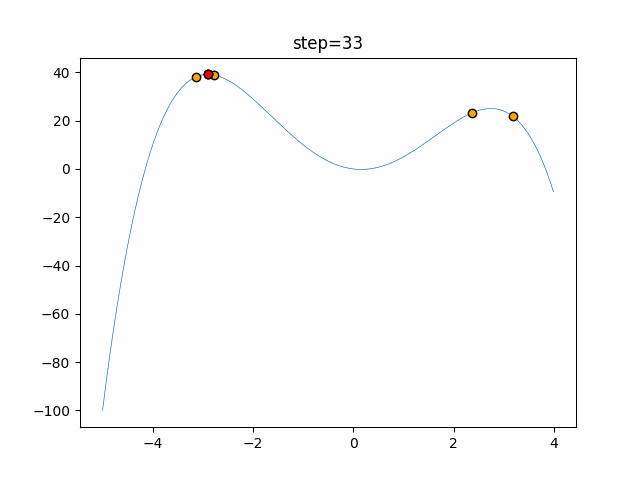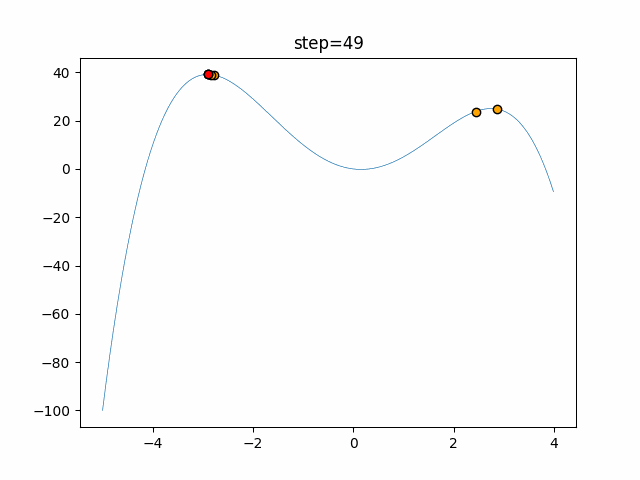
- 2D
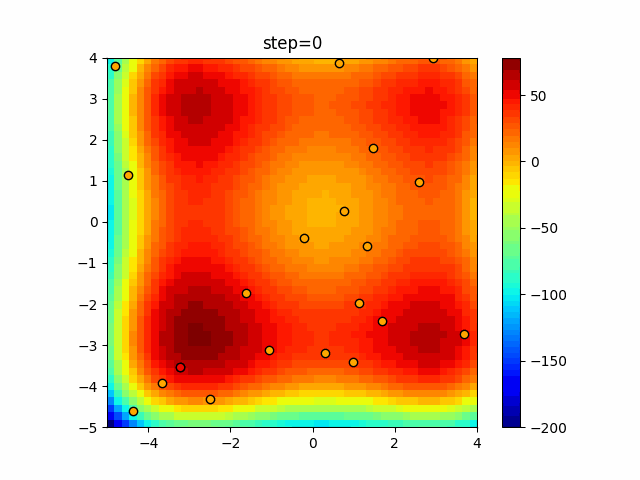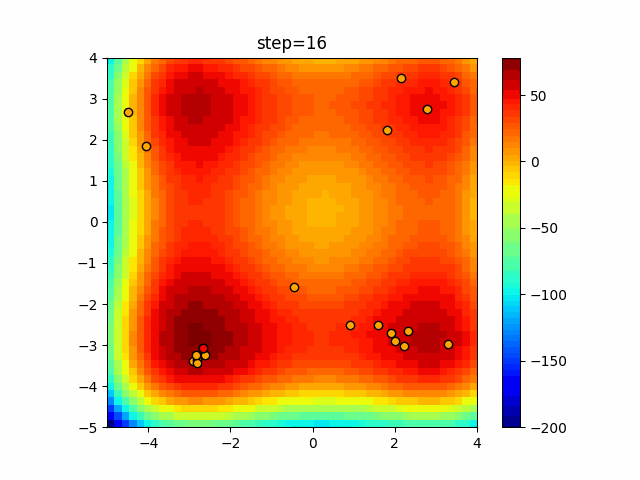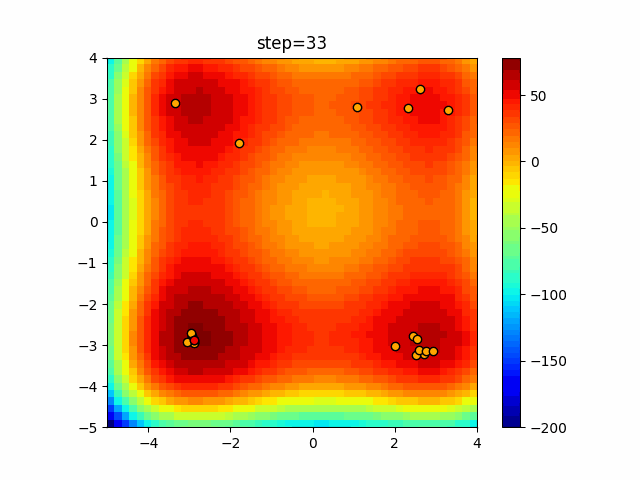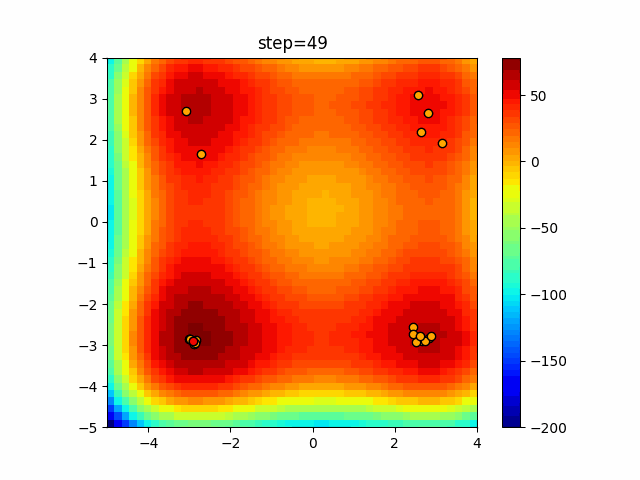
function_XinSheYang
- 1D
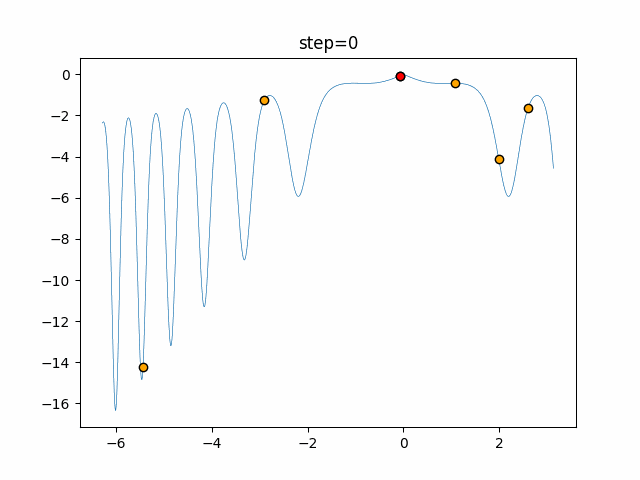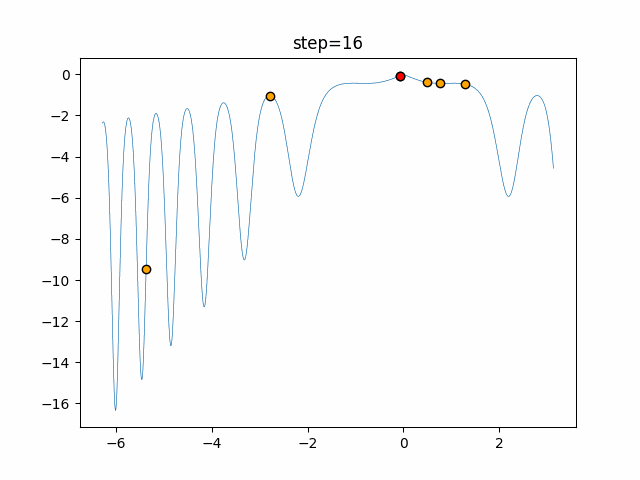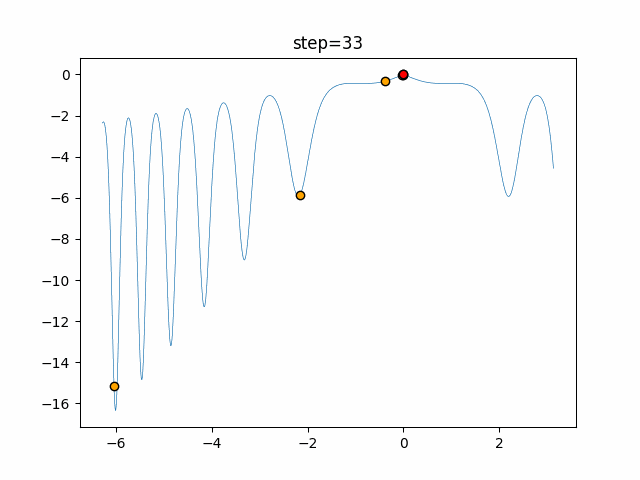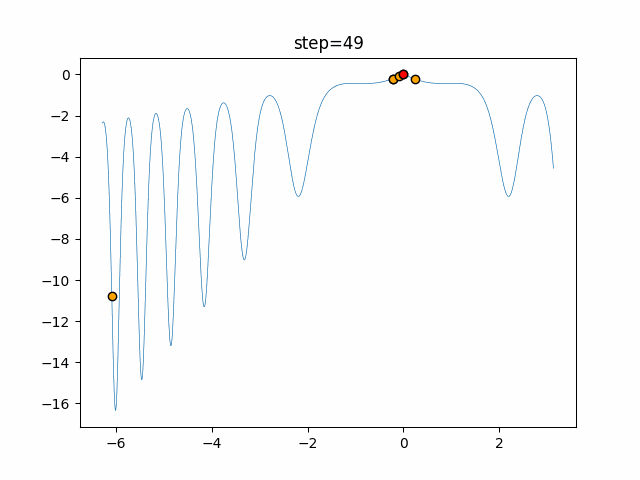
- 2D
Afterword
Since the image has a low alpha setting, it is difficult to get out of the local solution. It's nice that the fluffy feeling is like a firefly.
Recommended Posts