We will implement an optimization algorithm (differential evolution)
Introduction
A series of optimization algorithm implementations. First, look at Overview.
The code is on github.
Differential evolution
Differential evolution (DE) is a technique similar to the genetic algorithm devised based on the evolution of living organisms.
There are three major phases: Mutation, Crossover, and Selection. It seems that there are various algorithms for each phase like the genetic algorithm, but in this article, we implement it with the simplest algorithm.
reference ・ Hyperparameter tuning by differential evolution ・ Differential evolution (Wikipedia)
- Algorithm flow

- Term correspondence
| problem | Differential evolution |
|---|---|
| Array of input values | Agent position |
| Input value | Agent |
| Evaluation value | エージェントのEvaluation value |
- Regarding hyperparameters
| Variable name | meaning | Impressions |
|---|---|---|
| crossover_rate | Probability of crossing | Probability of becoming a mutation vector |
| scaling | Mutation vector scale factor(length) | The larger the size, the larger the range of movement |
Mutation
Create a mutation vector from three randomly selected agents.
import random
i =Index that represents you
#Randomly select 3 agents excluding the i-th
r1, r2, r3 = random.sample([ j for j in range(len(agents)) if j != i ], 3)
pos1 = agents[r1].getArray()
pos2 = agents[r2].getArray()
pos3 = agents[r3].getArray()
The mutation vector is calculated by the following formula.
$ F $ is a real number from 0 to 2 that represents the application rate (scaling factor) of the mutation difference. The python code is as follows.
#Numpy for easy vector calculation
import numpy as np
pos1 = np.asarray(pos1)
pos2 = np.asarray(pos2)
pos3 = np.asarray(pos3)
m_pos = pos1 + scaling * (pos2 - pos3)
Crossover
Cross at a binary crossover. It is a crossover that replaces the components with a certain probability (crossover_rate).
In addition, crossing always incorporates only one component on the mutation vector side.
import random
#Cross with mutation vector(Uniform crossing)
pos = agent.getArray()
ri = random.randint(0, len(pos)) #One component is always a mutation vector
for j in range(len(pos)):
if ri == j or random.random() < self.crossover_rate:
pos[j] = m_pos[j]
else:
pass #Do not update
#Create agent in new location
new_agent = problem.create(pos)
Survival choice
Compare the new agent created by the cross with the current agent and replace it if it has been updated.
#Replace if good individual
if agents[i].getScore() < new_agent.getScore():
agents[i] = new_agent
Whole code
The whole code. Since it is classified, it is a little different from the above code.
import math
import random
import numpy as np
class DE():
def __init__(self,
agent_max, #Number of agents
crossover_rate=0.5, #Crossover rate
scaling=0.5, #Difference application rate
):
self.agent_max = agent_max
self.crossover_rate = crossover_rate
self.scaling = scaling
def init(self, problem):
self.problem = problem
#Initial position generation
self.agents = []
for _ in range(self.agent_max):
self.agents.append(problem.create())
def step(self):
for i, agent in enumerate(self.agents):
#Randomly select 3 individuals that do not contain i
r1, r2, r3 = random.sample([ j for j in range(len(self.agents)) if j != i ], 3)
pos1 = self.agents[r1].getArray()
pos2 = self.agents[r2].getArray()
pos3 = self.agents[r3].getArray()
#Generate mutation vector from 3 individuals
pos1 = np.asarray(pos1)
pos2 = np.asarray(pos2)
pos3 = np.asarray(pos3)
m_pos = pos1 + self.scaling * (pos2 - pos3)
#Cross with mutation vector(Uniform crossing)
pos = agent.getArray()
ri = random.randint(0, len(pos)) #One component is always a mutation vector
for j in range(len(pos)):
if ri == j or random.random() < self.crossover_rate:
pos[j] = m_pos[j]
else:
pass #Do not update
#Replace if good individual
new_agent = self.problem.create(pos)
self.count += 1
if agent.getScore() < new_agent.getScore():
self.agents[i] = new_agent
Hyperparameter example
It is the result of optimizing hyperparameters with optuna for each problem. A single optimization attempt yields results with a search time of 2 seconds. I did this 100 times and asked optuna to find the best hyperparameters.
| problem | agent_max | crossover_rate | scaling |
|---|---|---|---|
| EightQueen | 5 | 0.008405098138137779 | 1.7482804860765253 |
| function_Ackley | 36 | 0.4076390525351224 | 0.2908895854800526 |
| function_Griewank | 14 | 0.27752386128521395 | 0.4629100940098222 |
| function_Michalewicz | 12 | 0.1532879607238835 | 0.0742830755371933 |
| function_Rastrigin | 28 | 0.33513859646880306 | 0.0754225020709786 |
| function_Schwefel | 13 | 0.00032331965923372563 | 0.13153649005308807 |
| function_StyblinskiTang | 39 | 0.21247741932099348 | 0.08732185323441227 |
| function_XinSheYang | 33 | 0.0955103914325307 | 0.008270969294347359 |
| LifeGame | 39 | 0.6612227467897149 | 1.136453380180552 |
| OneMax | 4 | 0.1190487045395953 | 1.1581036102901494 |
| TSP | 23 | 0.41212989299137665 | 0.014644735558753091 |
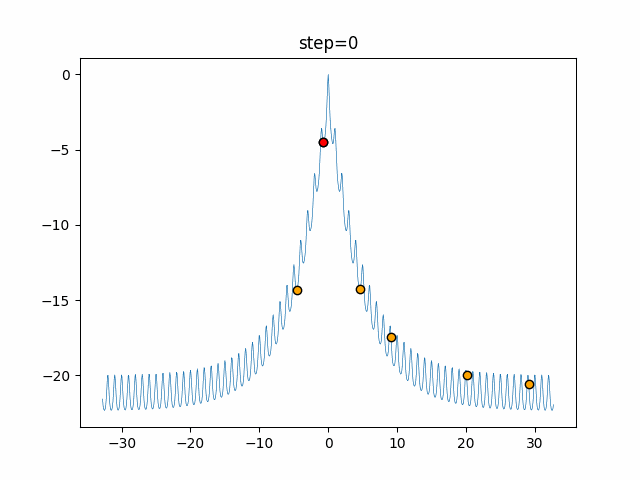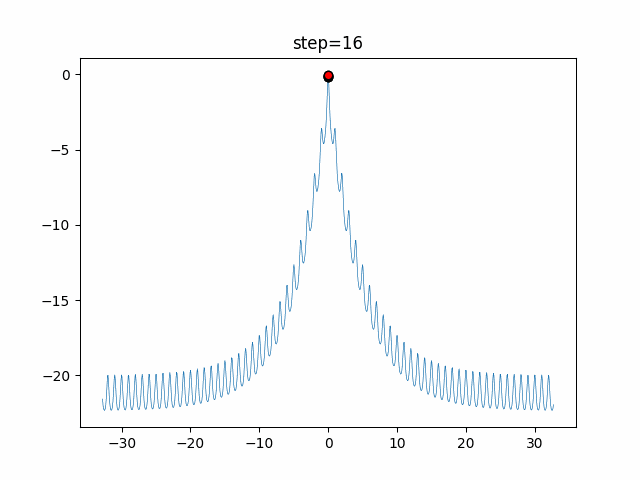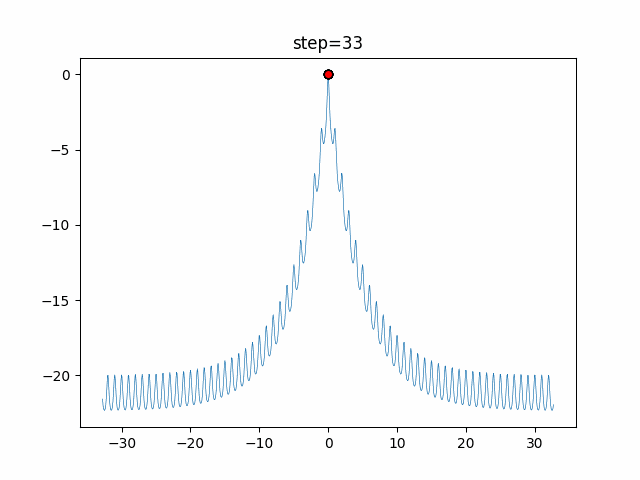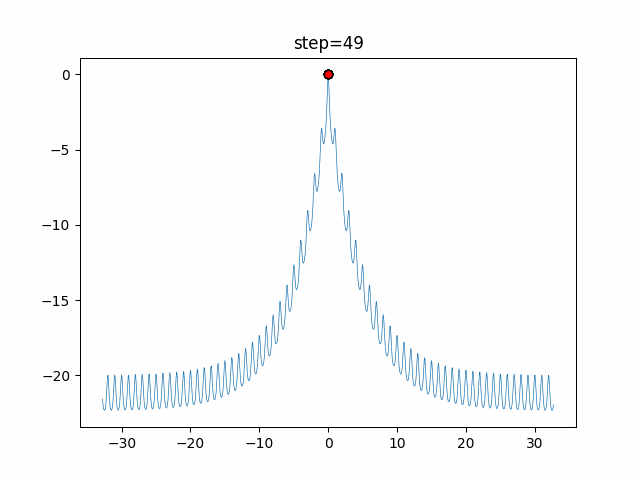
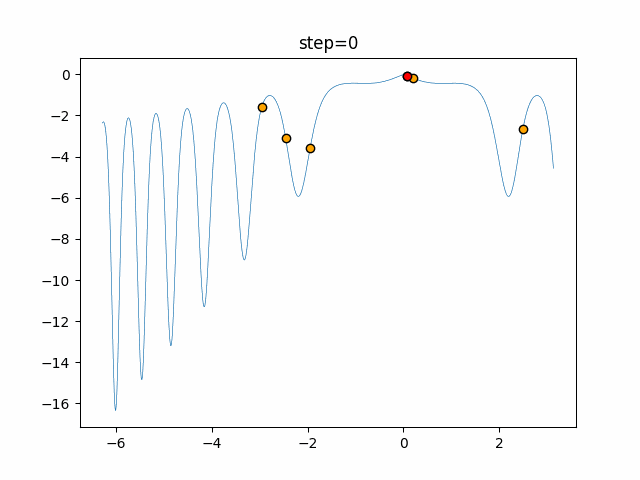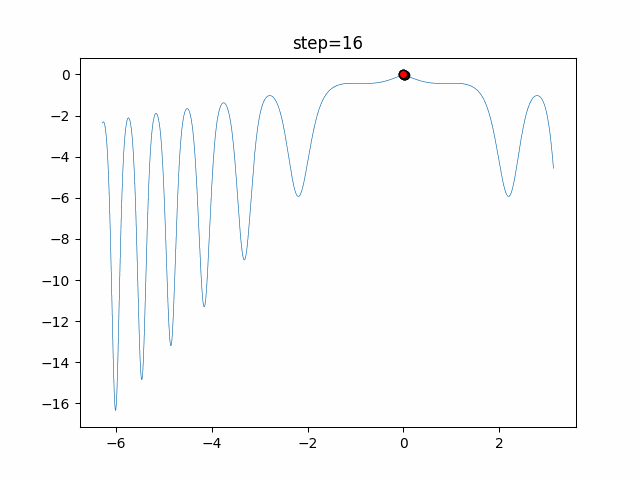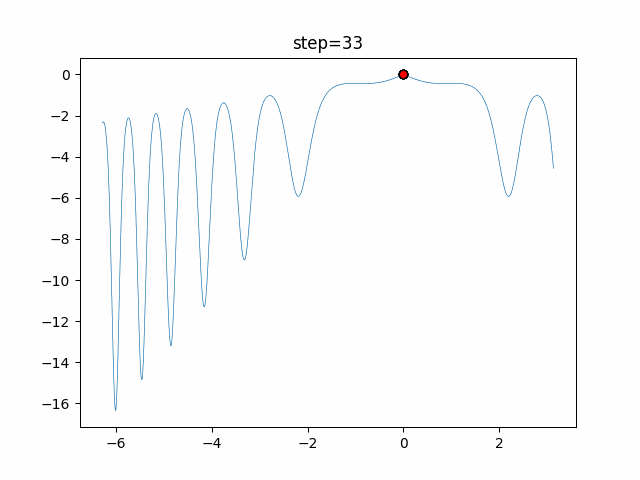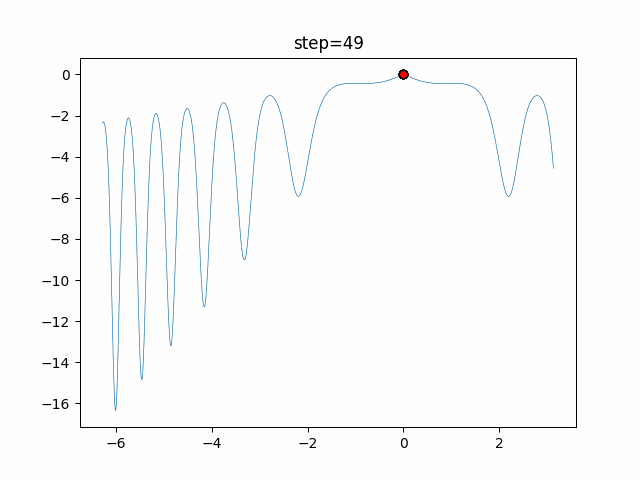
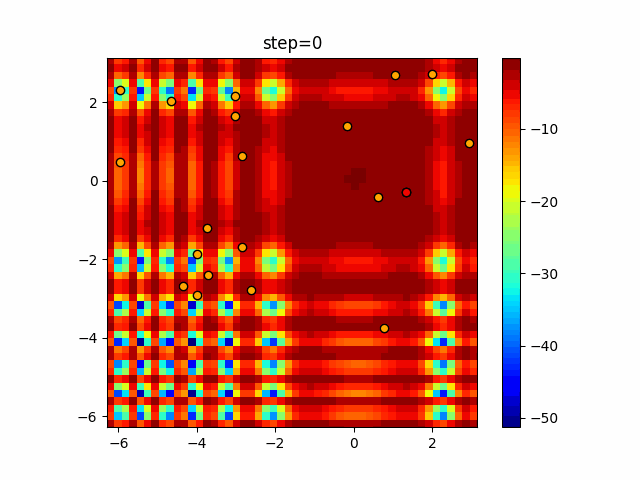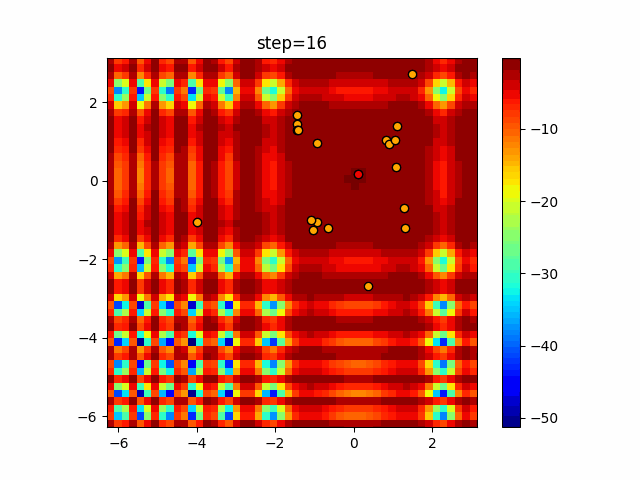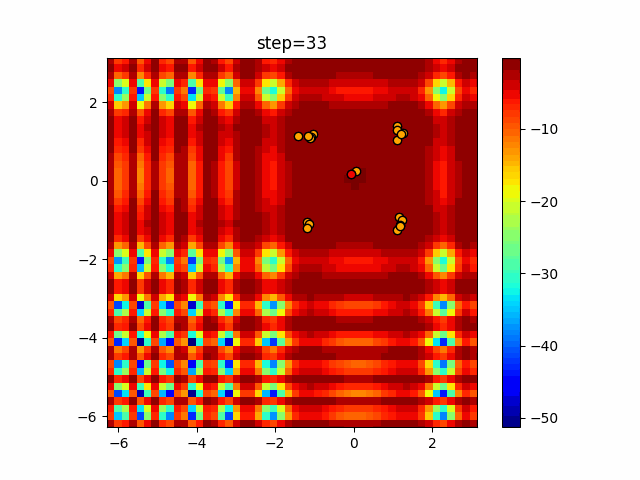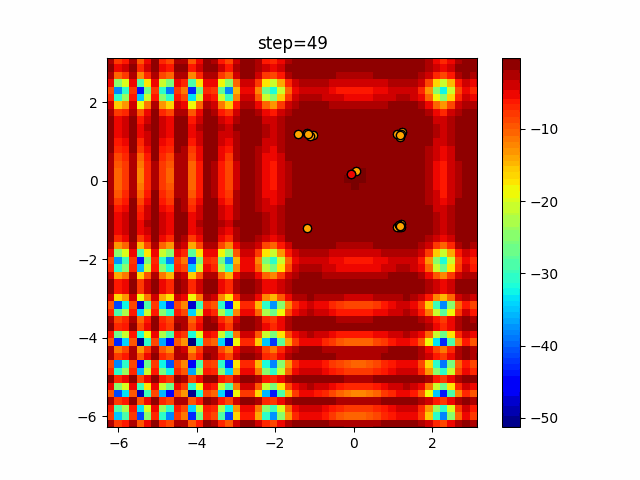
Visualization of actual movement
The 1st dimension is 6 individuals, and the 2nd dimension is 20 individuals, which is the result of 50 steps. The red circle is the individual with the highest score in that step.
The parameters were executed below.
DE(N, crossover_rate=0, scaling=0.4)
function_Ackley
- 1D
- 2D
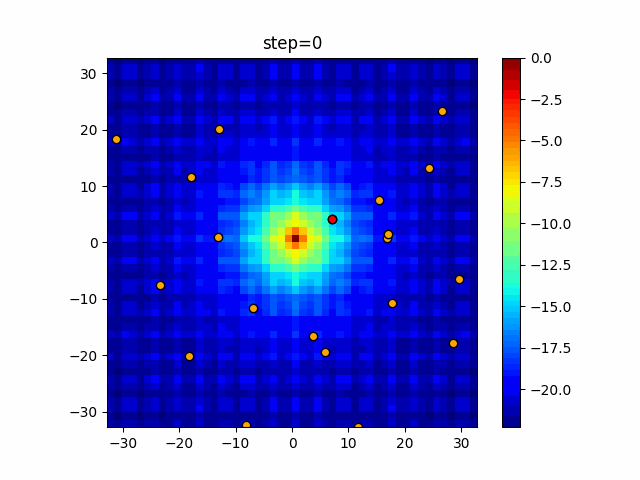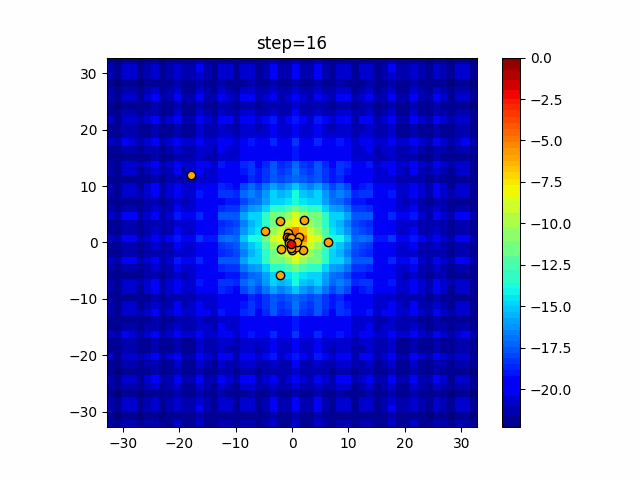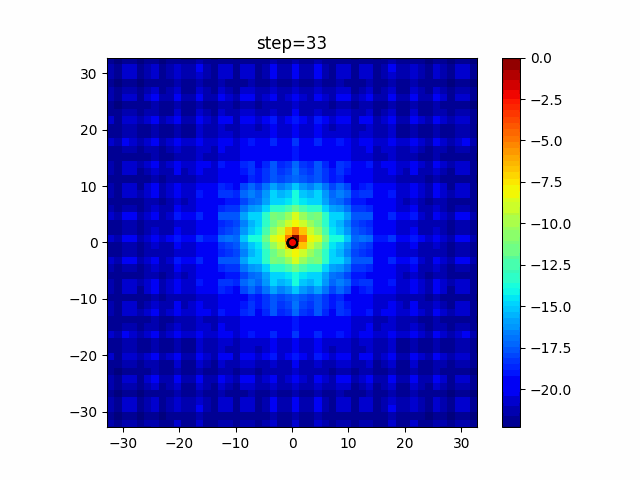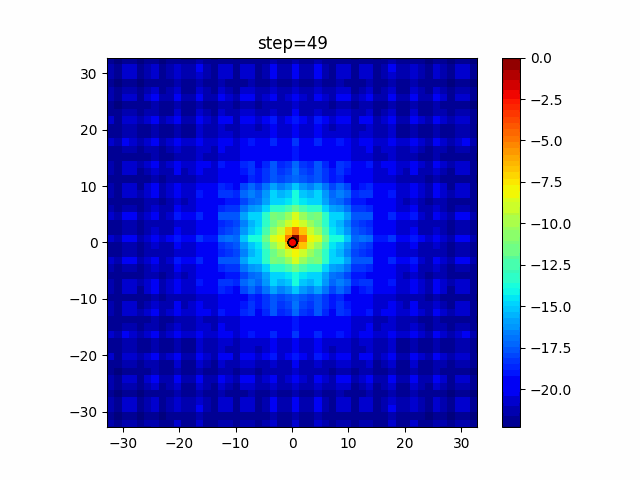
function_Rastrigin
- 1D
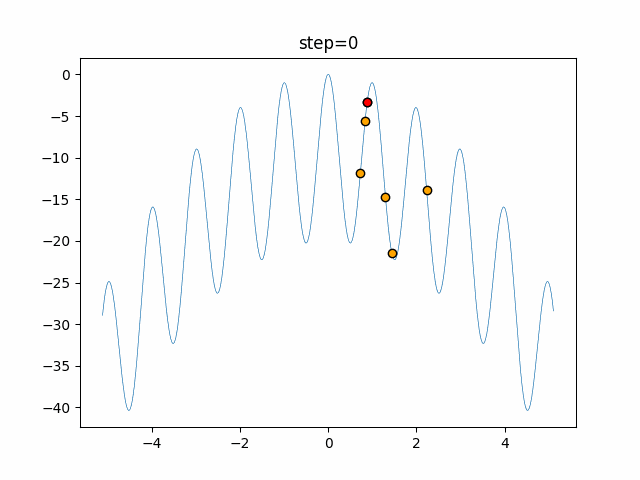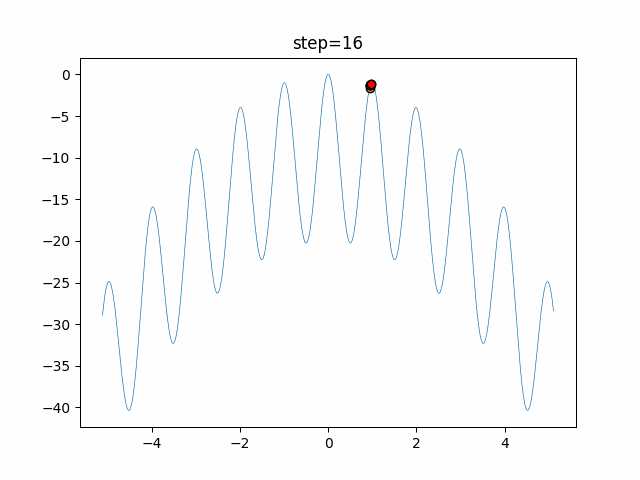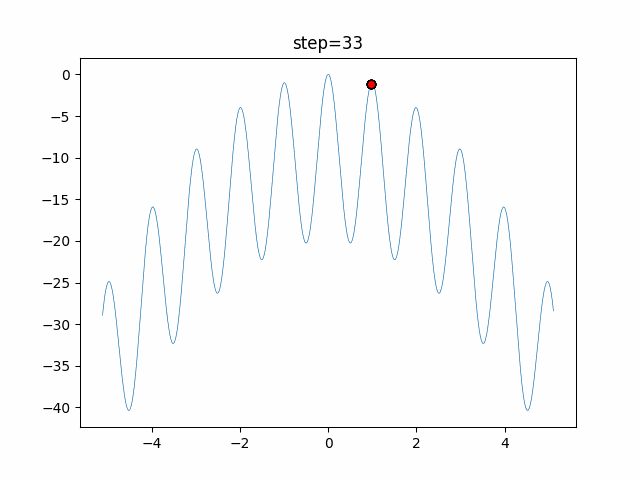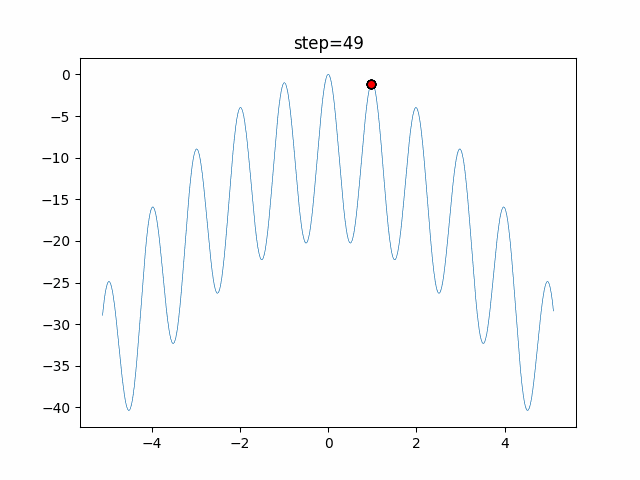
- 2D
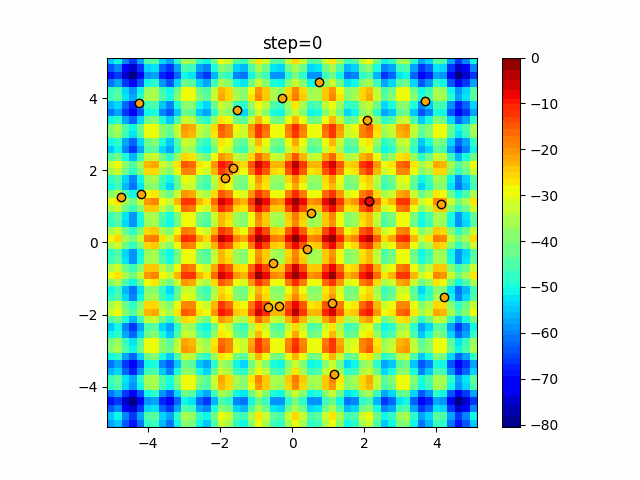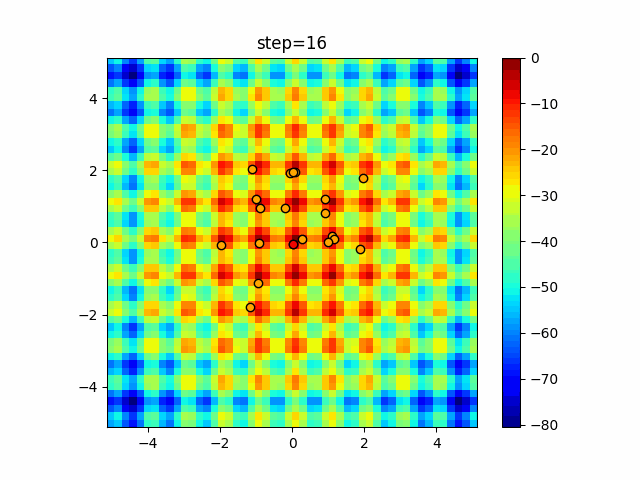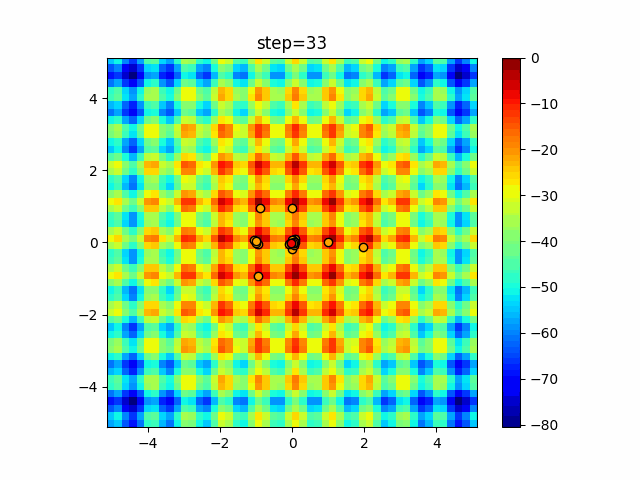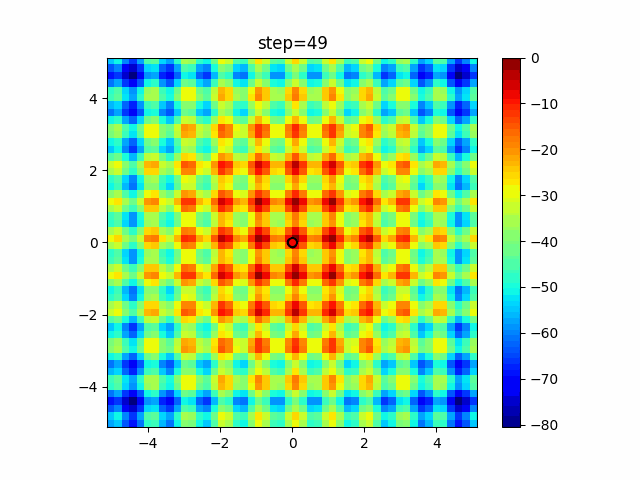
function_Schwefel
- 1D
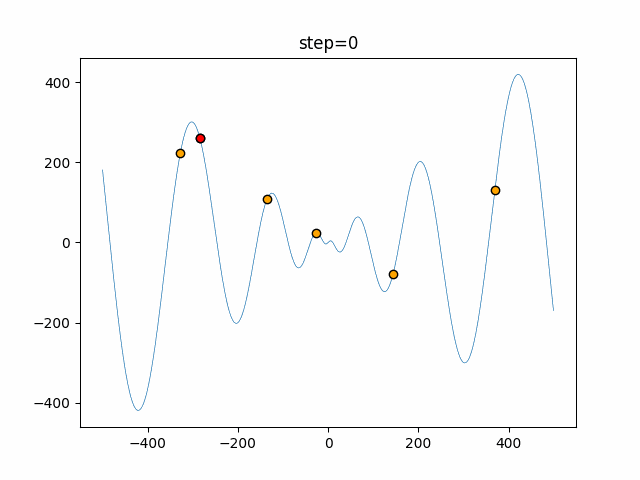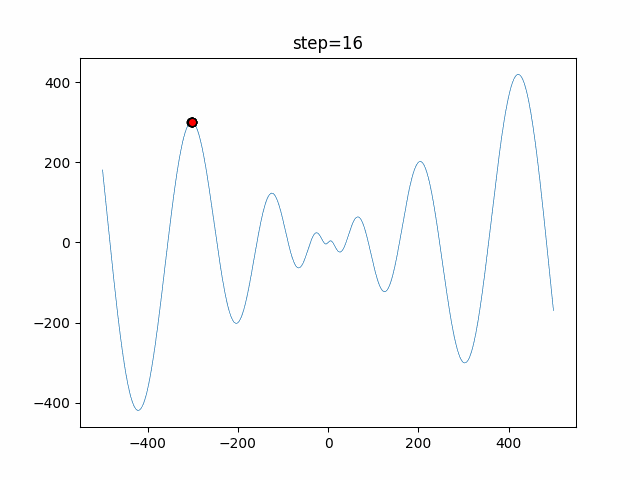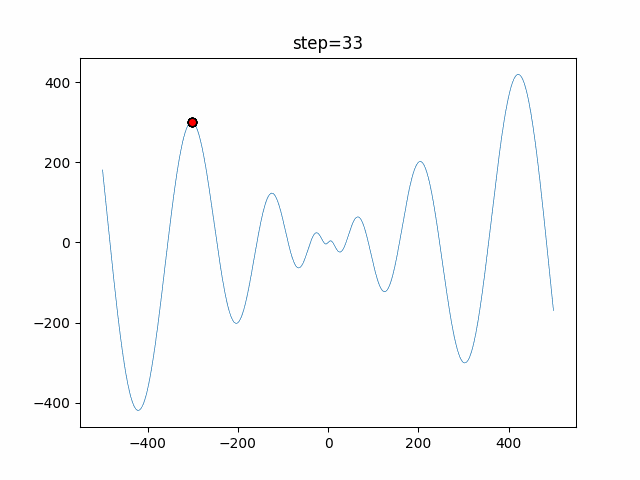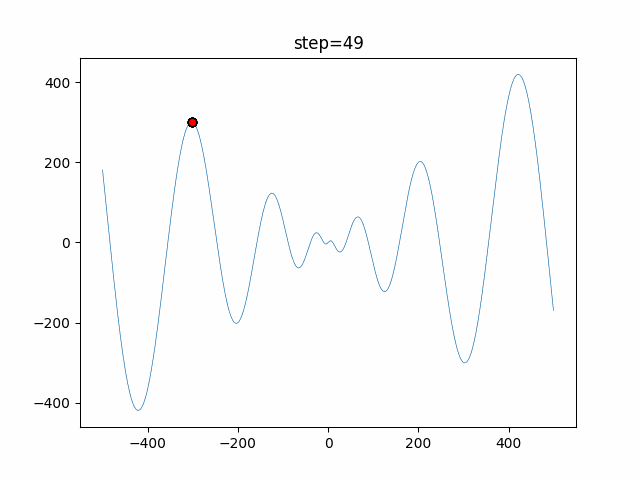
- 2D
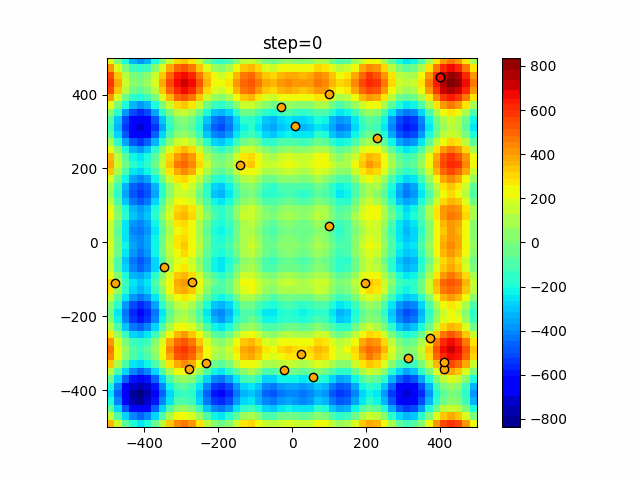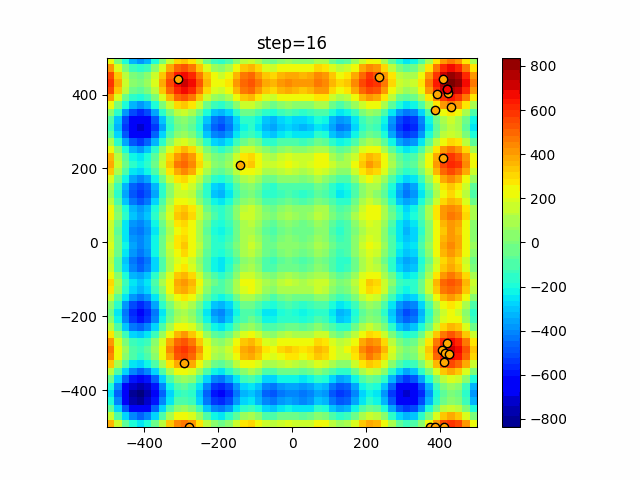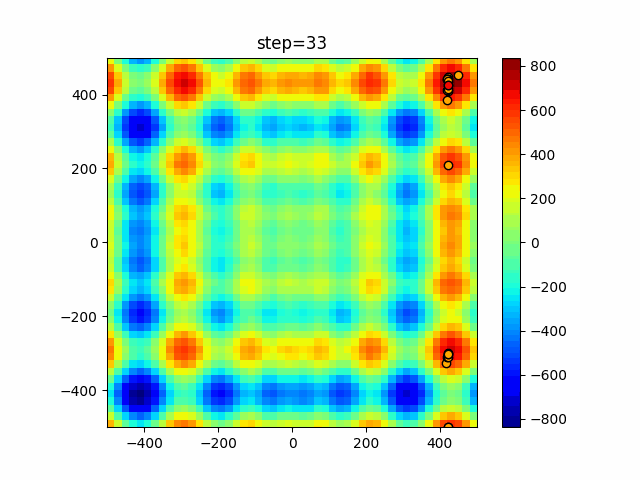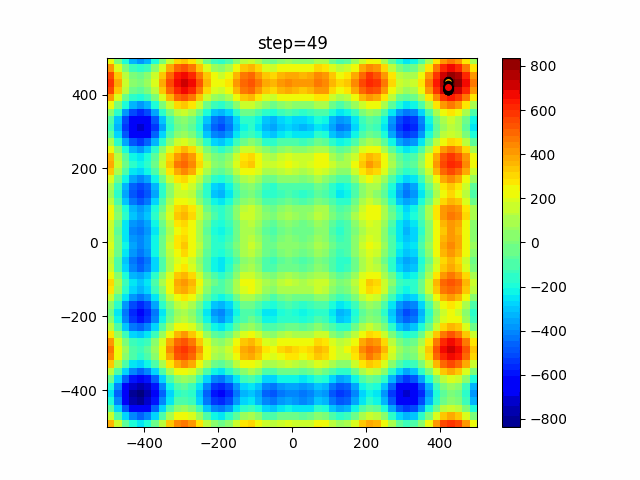
function_StyblinskiTang
- 1D
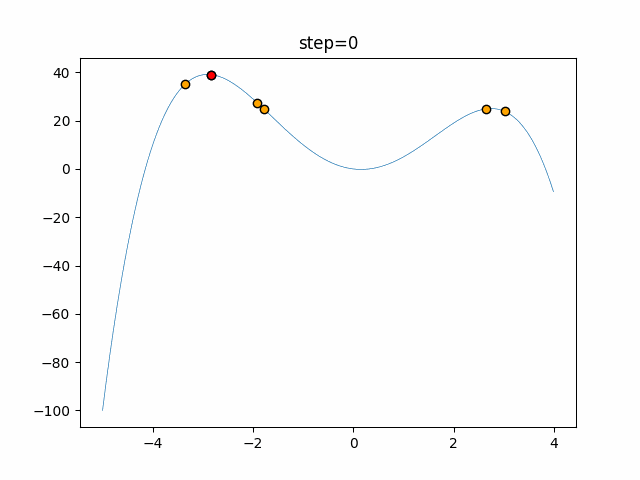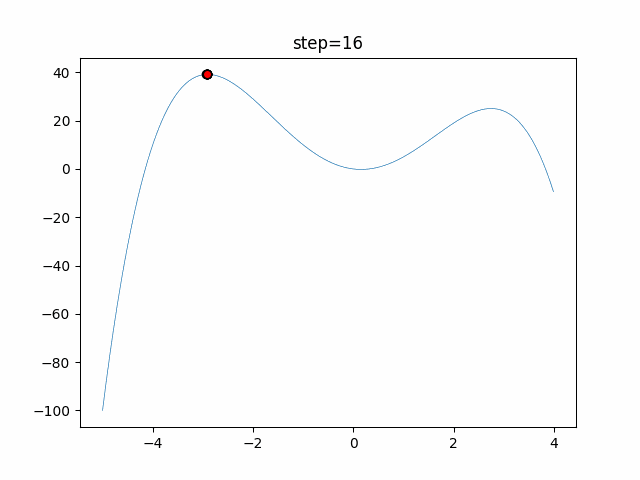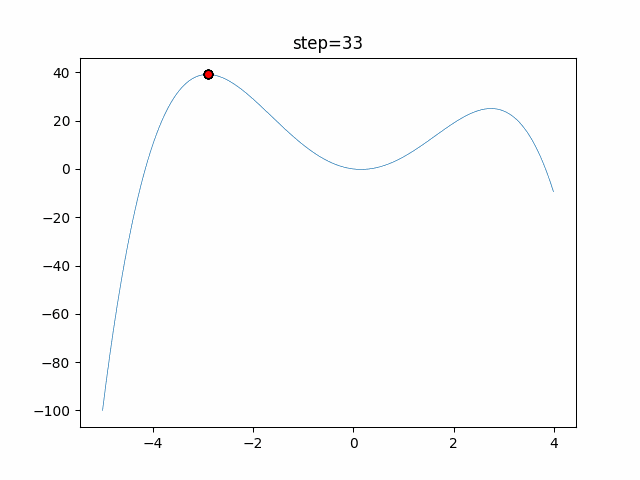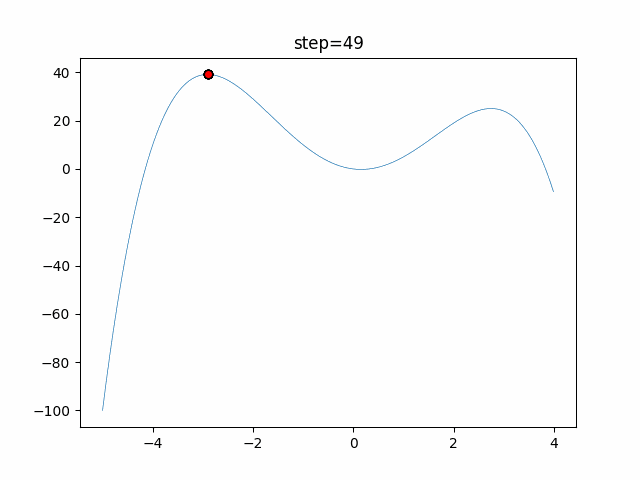
- 2D
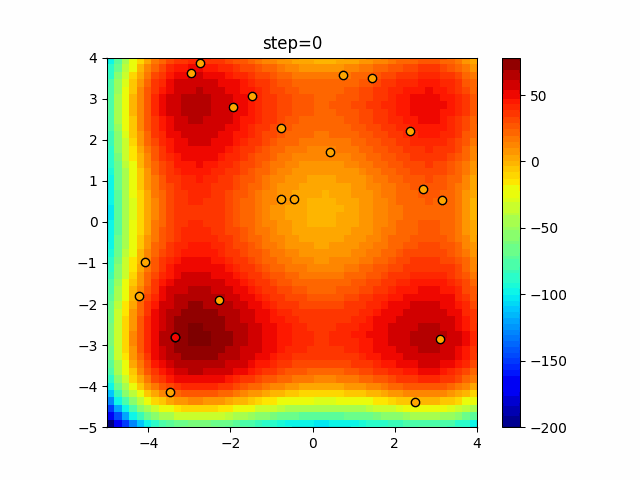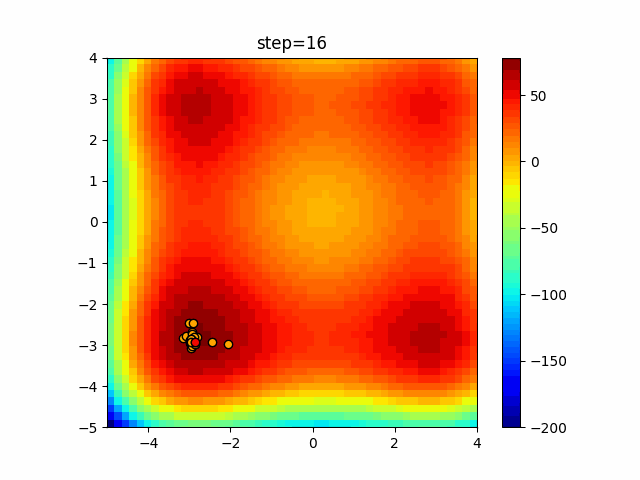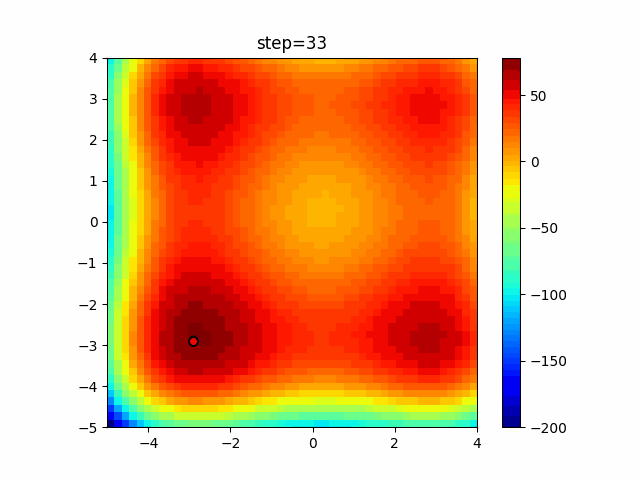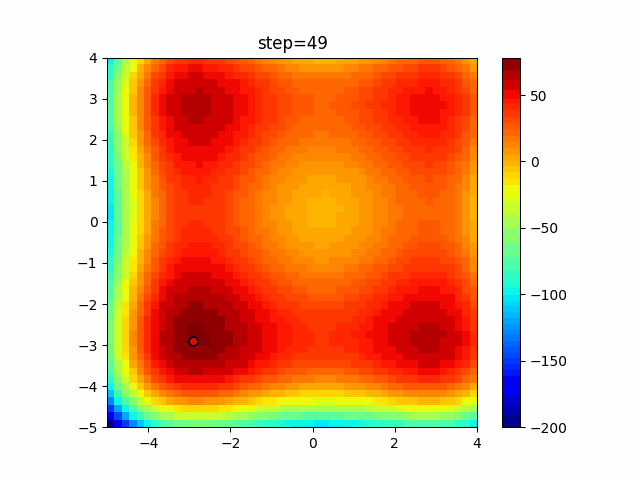
function_XinSheYang
- 1D
- 2D
Afterword
It will converge to a good feeling. However, since there is no random movement, I feel that it is easy to fall into a local solution.
Recommended Posts