We will implement the optimization algorithm (bat algorithm)
Introduction
A series of optimization algorithm implementations. First, look at Overview.
The code can be found on github.
Bat algorithm
The Bat Algorithm is an algorithm that focuses on echo-localization behavior in which bats use ultrasonic waves to locate prey and obstacles.
Bats decide their behavior based on four factors: speed, frequency, pulse rate, and volume.
- Algorithm flow


- Term correspondence
| problem | Bat algorithm |
|---|---|
| Array of input values | Position of bats |
| Input value | Bat |
| Evaluation value | コウモリの位置におけるEvaluation value |
- Meaning of variables used in code
| Variable name | meaning | Impressions |
|---|---|---|
| problem | Any problem class (see problem section) | |
| bat_max | Number of bats | |
| frequency_min | Minimum frequency | Lower limit of migration rate to best bats |
| frequency_max | Maximum frequency | Upper limit of the rate of movement to the best bat |
| good_bat_rate | Percentage of good bats | |
| volume_init | Initial value of volume | The louder the volume, the stronger the random number and the wider the area |
| volume_update_rate | Volume reduction rate | Volume decreases with time |
| pulse_convergence_value | Convergent value of pulse rate | The pulse rate is the probability of moving closer to a good bat, and if the convergence value is 1, it will eventually stop moving. |
| pulse_convergence_speed | Speed of convergence of pulse rate | 0.5 is 10 times, 0.If it is 2, it will converge in about 20 times |
Get closer to the best bats
To move to the best bat, update the speed based on the difference and frequency between the position of the best bat and your position, and move using that speed.
$ \ Vec {v_i} $ is the velocity, $ \ vec {x_i} $ is the position, and $ \ vec {g} $ is the best bat position.
The frequency is a random number between the lower limit ($ f_ {min}
import random
import numpy as np
#frequency
frequency = frequency_min + (frequency_max - frequency_min) * random.random()
pos_best = np.asarray(best_bat.getArray())
pos = np.asarray(bat["bat"].getArray())
#Calculate speed
bat["v"] = bat["v"] + frequency * (pos_best - pos)
#Update position and create bats in new position
new_bat1 = problem.create(pos + bat["v"])
Move near a good bat
It is a good move to a bat, but first compare the pulse rate and the random number, and if it is above the random number, it will not move.
If you want to move, first choose a good bat. Good bats are randomly selected from the top few percent of all bats.
Then move closer to a good bat.
Where $ \ bar {A} $ is the average volume of all bats and $ \ vec {\ epsilon} $ is a random vector from -1 to 1.
import random
import numpy as np
new_bat2 = None
#Move closer to a good bat with a random number
if bat["pulse"] < random.random():
#Sort
bats.sort(key=lambda x: x["bat"].getScore())
#Randomly choose good bats
r = random.randint(1, good_bat_num)
pos_good = np.asarray(bats[-r]["bat"].getArray())
#Average volume of all bats
volume = np.average([x["volume"] for x in self.bats])
rn = np.random.uniform(-1, 1, len(pos_good)) # -1,Random number of 1
new_pos2 = pos_good + volume * rn
new_bat2 = problem.create(new_pos2)
update
The update formula for the pulse rate ($ r_i $) is as follows.
$ R_0 $ is the convergence value of the pulse rate (constant), and $ \ gamma $ is the speed of convergence of the pulse rate (constant).
Also, the update formula for the volume ($ A_i $) is as follows.
$ \ Alpha $ is the rate (constant) that reduces the volume.
Updates will be made according to the algorithm flow chart.
import random
volume_update_rate = 0.9
pulse_convergence_value = 0.5
pulse_convergence_speed = 0.9
def _calcPulse(count):
return pulse_convergence_value * (1-math.exp(-pulse_convergence_speed*count))
#Randomly generate new positions
new_bat3 = problem.create()
score1 = new_bat1.getScore()
score2 = None if new_bat2 is None else new_bat2.getScore()
score3 = new_bat3.getScore()
if (score2 is None or score1 > score2) and score1 > score3 :
#Random number of volume
if random.random() < bat["volume"]:
if score2 is None or score2 <= score3:
#Update at random position
bat["bat"] = new_bat3
else:
#Updated at a location near a good bat
bat["bat"] = new_bat3
#Pulse rate update
bat["pulse"] = _calcPulse(step_count)
#Volume update
bat["volume"] = volume_update_rate * bat["volume"]
else:
#Updated in position to the best bat
bat["bat"] = new_bat1
else:
#Updated in position to the best bat
bat["bat"] = new_bat1
#Step count+1
step_count += 1
About pulse rate
The pulse rate changes as follows depending on the convergence speed. (When pulse_convergence_value = 1) Even if it is 0.2, it will converge in about 20 times, and it will converge fairly quickly, so a small value may be good.

Whole code
import math
import random
import numpy as np
class Bat():
def __init__(self,
bat_max,
frequency_min=0,
frequency_max=1,
good_bat_rate=0.2,
volume_init=1.0,
volume_update_rate=0.9,
pulse_convergence_value=0.5,
pulse_convergence_speed=0.9,
):
self.bat_max = bat_max
self.frequency_min = frequency_min
self.frequency_max = frequency_max
self.good_bat_num = int(bat_max * good_bat_rate + 0.5)
if self.good_bat_num > bat_max:
self.good_bat_num = bat_max
if self.good_bat_num < 1:
self.good_bat_num = 1
self.volume_init = volume_init
self.volume_update_rate = volume_update_rate
self.pulse_convergence_value = pulse_convergence_value
self.pulse_convergence_speed = pulse_convergence_speed
def init(self, problem):
self.problem = problem
self.count = 0
self.step_count = 0
self.best_bat = None
self.bats = []
for _ in range(self.bat_max):
o = problem.create()
d = {
"bat": o,
"pulse": self._calcPulse(0),
"volume": self.volume_init,
"v": np.zeros(problem.size)
}
self.bats.append(d)
if self.best_bat is None or self.best_bat.getScore() < o.getScore():
self.best_bat = o
def _calcPulse(self, count):
return self.pulse_convergence_value*(1-math.exp(-self.pulse_convergence_speed*count))
def step(self):
self.bats.sort(key=lambda x: x["bat"].getScore())
for bat in self.bats:
#frequency
frequency = self.frequency_min + (self.frequency_max - self.frequency_min) * random.random()
#Get closer to the best bats
pos_best = self.best_bat.getArray()
pos = bat["bat"].getArray()
bat["v"] = bat["v"] + frequency * (pos_best - pos)
new_bat1 = self.problem.create(pos + bat["v"])
#Volume judgment
if random.random() >= bat["volume"]:
#Update in new position
bat["bat"] = new_bat1
#Best bat check
if self.best_bat.getScore() < bat["bat"].getScore():
self.best_bat = bat["bat"]
continue
#Move closer to a good bat with a random number
new_bat2 = None
if bat["pulse"] < random.random():
#Average volume of all bats
volume = np.average([x["volume"] for x in self.bats])
#Choose a good bat
r = random.randint(1, self.good_bat_num)
pos_good = self.bats[-r]["bat"].getArray()
rn = np.random.uniform(-1, 1, len(pos_good)) # -1,Random number of 1
new_bat2 = self.problem.create(pos_good + volume * rn)
#Randomly generated
new_bat3 = self.problem.create()
#Comparison of new positions
score1 = new_bat1.getScore()
score2 = None if new_bat2 is None else new_bat2.getScore()
score3 = new_bat3.getScore()
if (score2 is None or score1 > score2) and score1 > score3 :
if score2 is None or score2 <= score3:
bat["bat"] = new_bat3
else:
bat["bat"] = new_bat2
#Pulse rate update
bat["pulse"] = self._calcPulse(self.step_count)
#Volume update
bat["volume"] = self.volume_update_rate * bat["volume"]
else:
bat["bat"] = new_bat1
#Best bat check
if self.best_bat.getScore() < bat["bat"].getScore():
self.best_bat = bat["bat"]
self.step_count += 1
Hyperparameter example
It is the result of optimizing hyperparameters with optuna for each problem. A single optimization attempt yields results with a search time of 2 seconds. I did this 100 times and asked optuna to find the best hyperparameters.
- Frequency_min is fixed at 0
| problem | bat_max | frequency_max | frequency_min | good_bat_rate | pulse_convergence_speed | pulse_convergence_value | volume_init | volume_update_rate |
|---|---|---|---|---|---|---|---|---|
| EightQueen | 21 | 0.16056311709148877 | 0.0 | 0.18895324827898902 | 0.7743073337572011 | 0.015299647553258189 | 0.37862199762341764 | 0.5219340167573981 |
| function_Ackley | 6 | 0.5807409179883148 | 0.0 | 0.8431315762963505 | 0.6168807797723693 | 0.41730375451852453 | 0.41343060460565206 | 0.15049946819845028 |
| function_Griewank | 8 | 0.9452402185165402 | 0.0 | 0.7201234515965615 | 0.7260546767194784 | 0.130926854366477 | 0.013897440965911972 | 0.018889941226347226 |
| function_Michalewicz | 49 | 0.4179217659403093 | 0.0 | 0.6361175345153247 | 0.5018316263776195 | 0.42459903007426236 | 0.4968382725357193 | 0.1065841508592828 |
| function_Rastrigin | 4 | 0.6140740614258697 | 0.0 | 0.08321822782531468 | 0.37791620723418984 | 0.5942334579901081 | 0.2272362640804505 | 0.6090017290739149 |
| function_Schwefel | 5 | 0.9974629382587714 | 0.0 | 0.48057178703432885 | 0.017850539098788976 | 0.8624933090356682 | 0.008382588455720222 | 0.9676085790533966 |
| function_StyblinskiTang | 9 | 0.9919883606063762 | 0.0 | 0.3096861786862085 | 0.6695497098867679 | 0.8832509763124465 | 1.3802416508441109 | 0.24307207412221196 |
| LifeGame | 17 | 0.17520950919099773 | 0.0 | 0.5512117484751708 | 0.3239752160390367 | 0.5877290654832432 | 0.6901442886406529 | 0.7052284742486757 |
| OneMax | 47 | 0.4118670851332011 | 0.0 | 0.4420165018547974 | 0.1217770472809899 | 0.8862495030963856 | 1.0185236105175342 | 0.5188797824478796 |
| TSP | 8 | 0.44386885244368085 | 0.0 | 0.19840772635097428 | 0.24715859136402973 | 0.3995313116893353 | 0.40899114232584255 | 0.00012730831532623 |
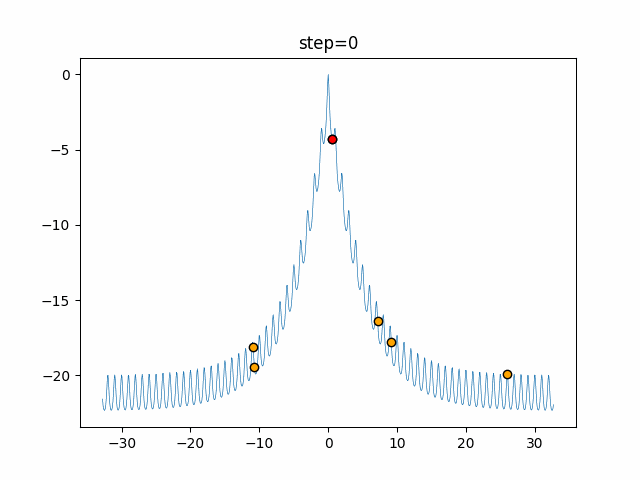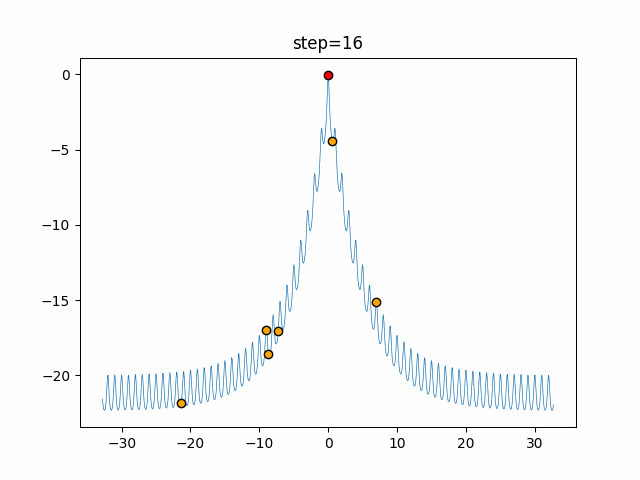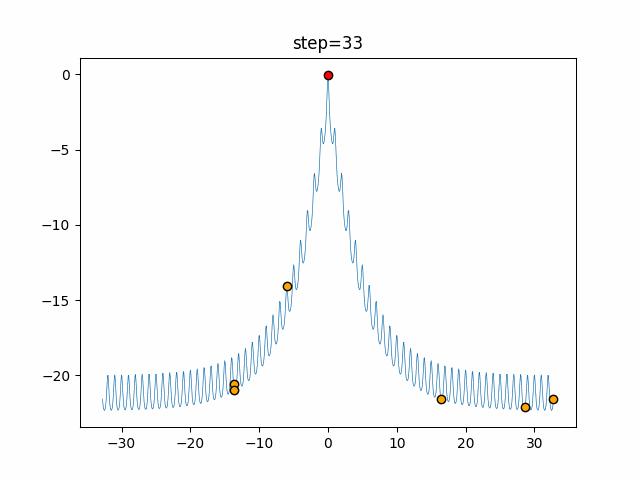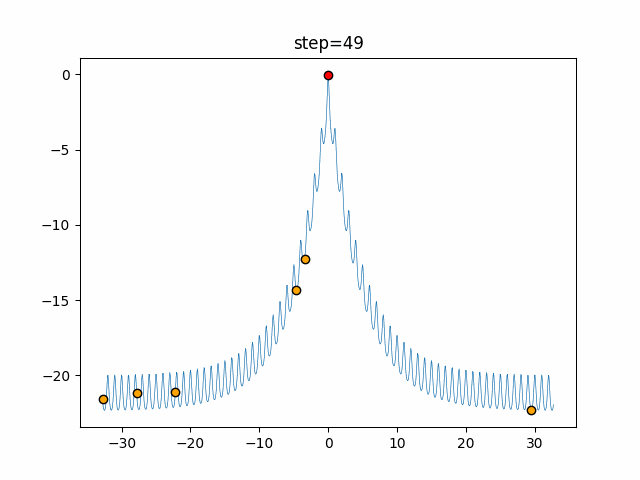
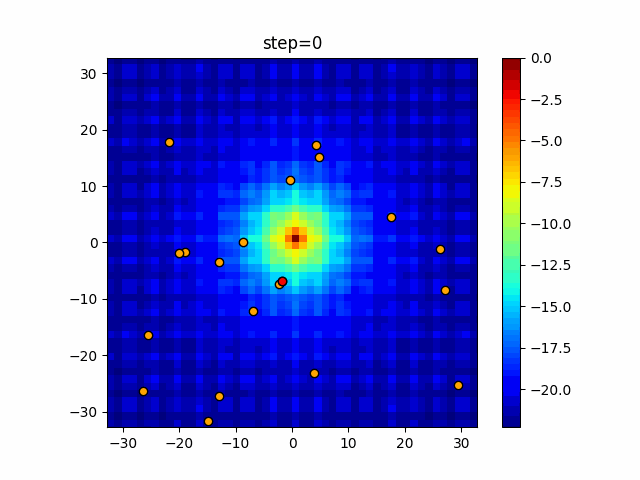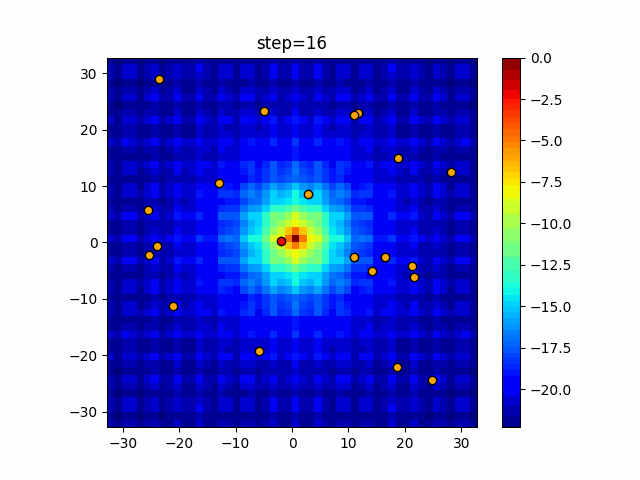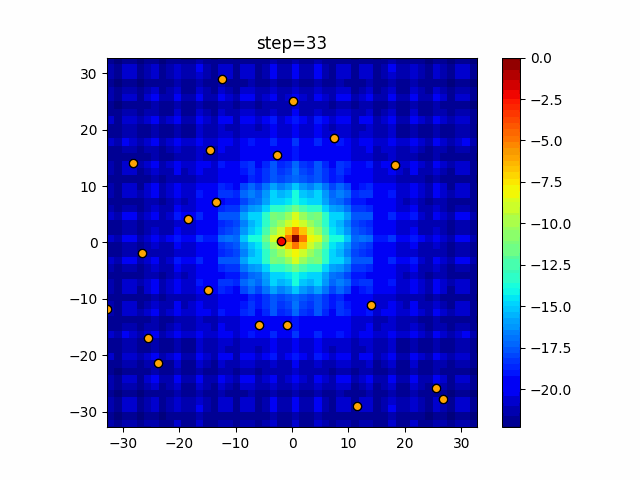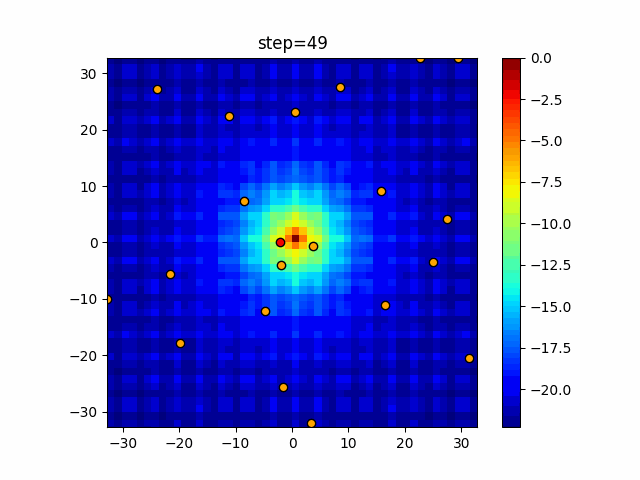
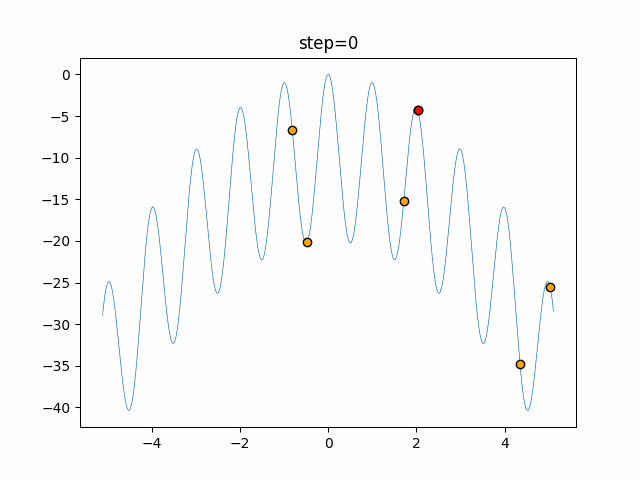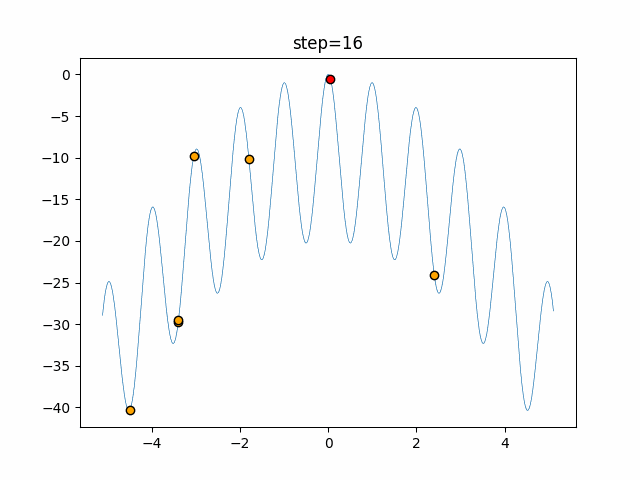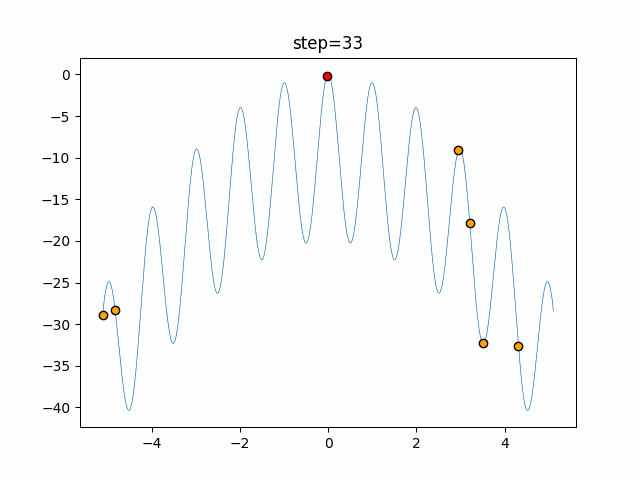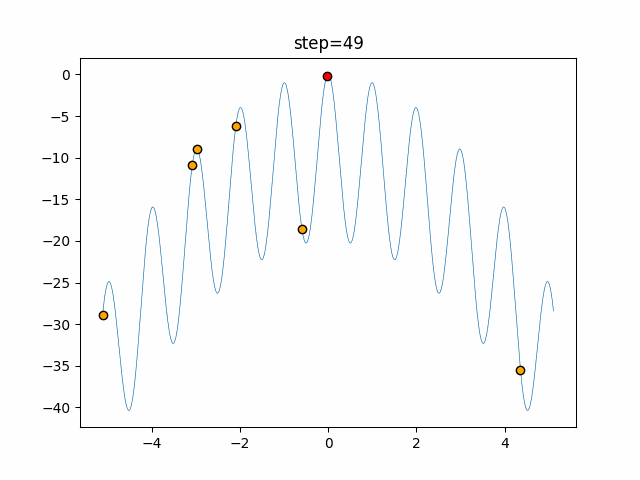
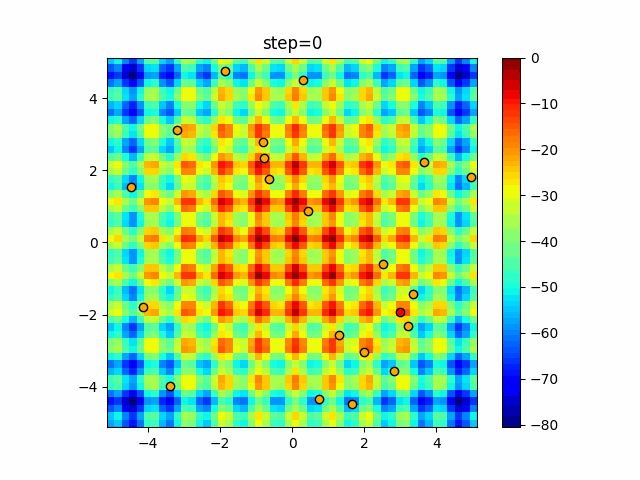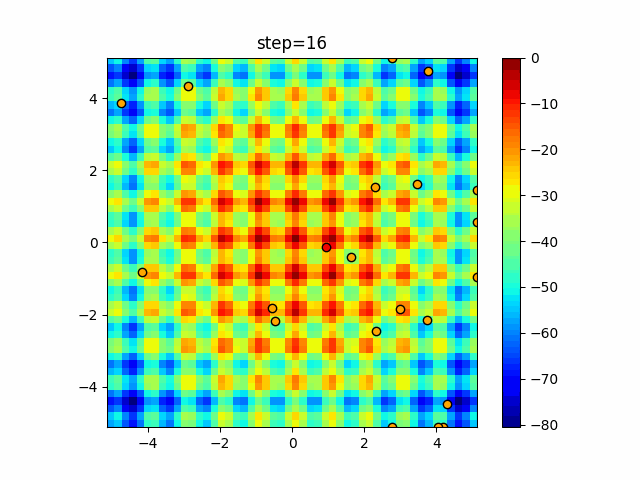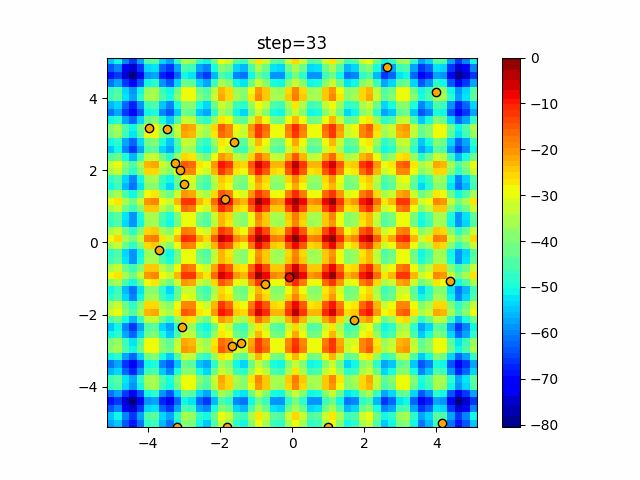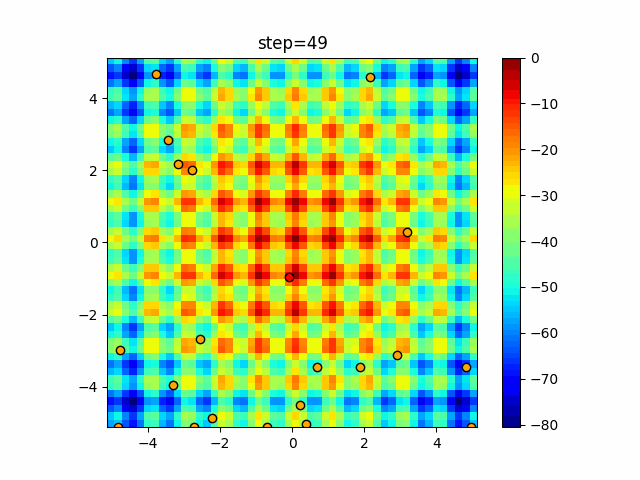
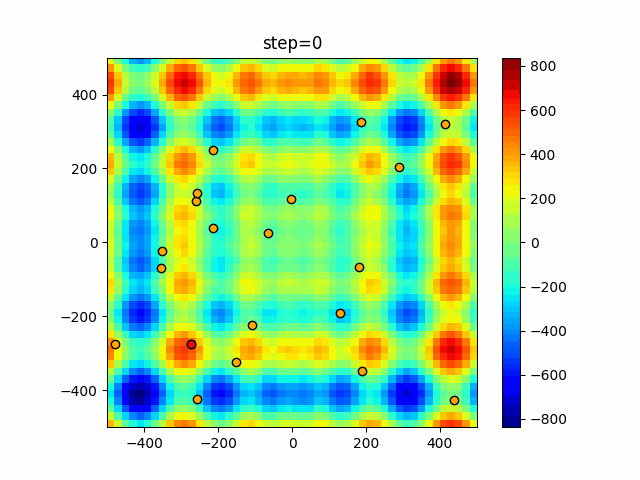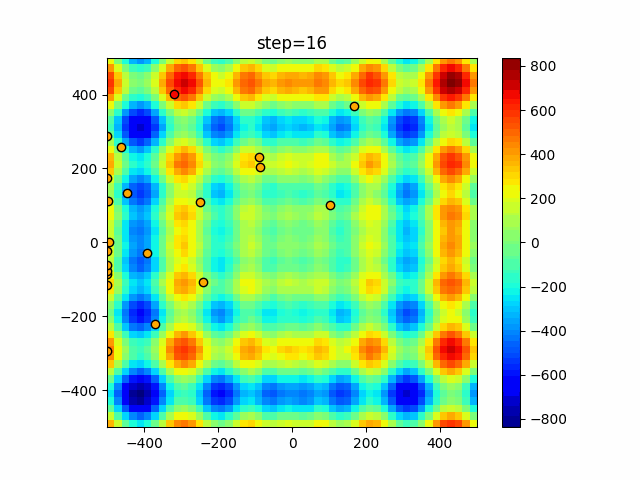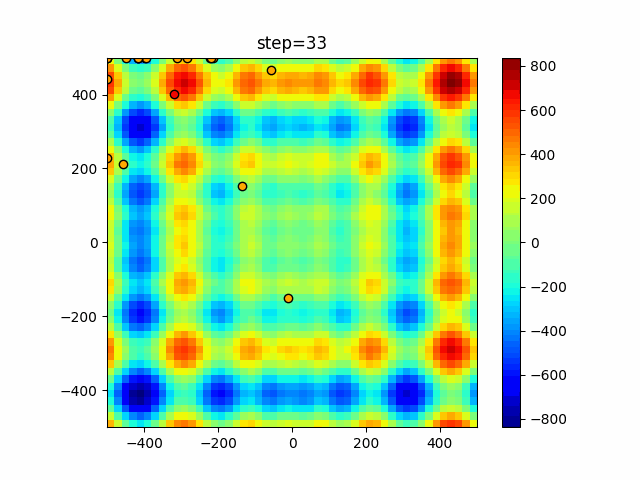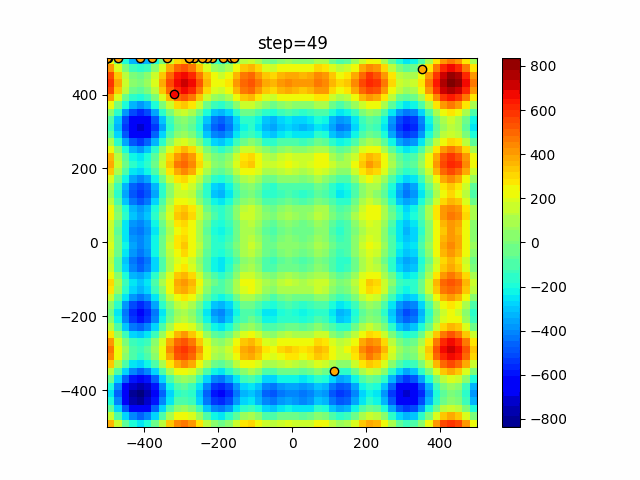
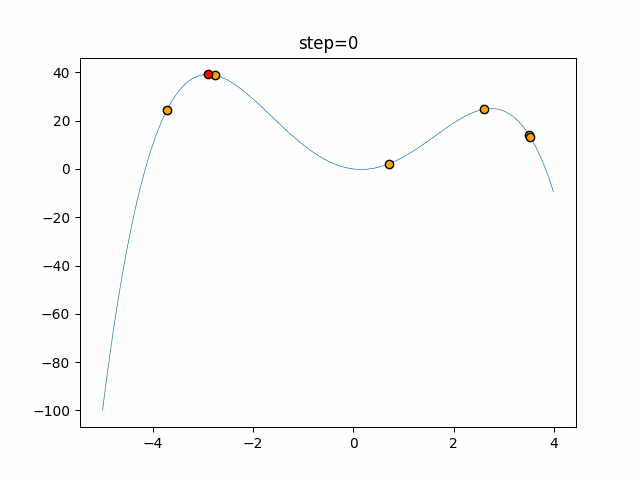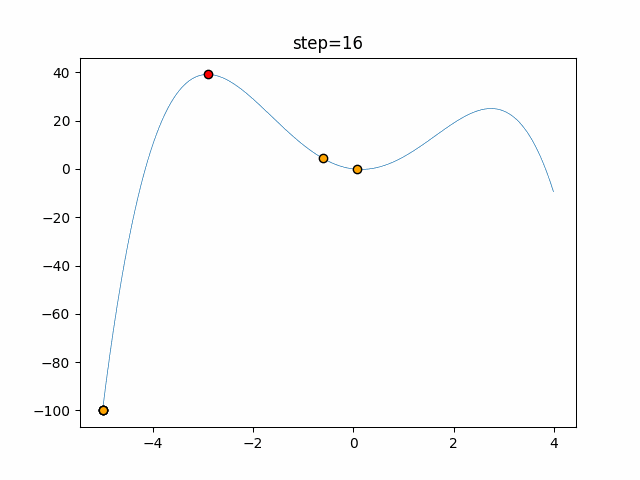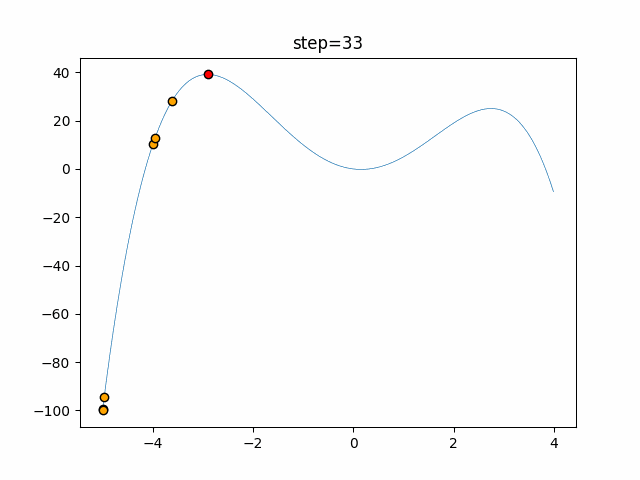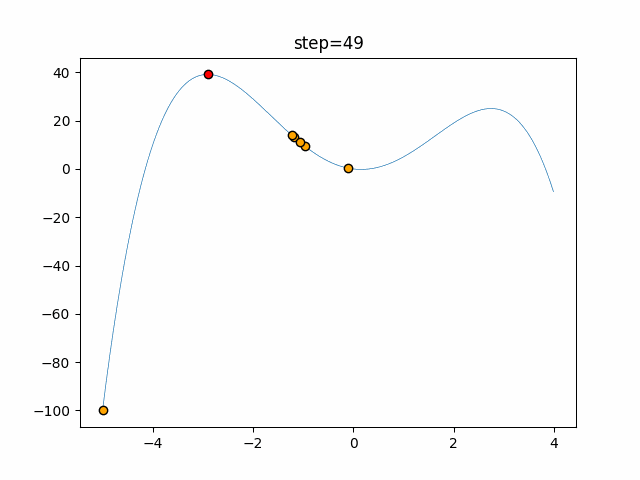
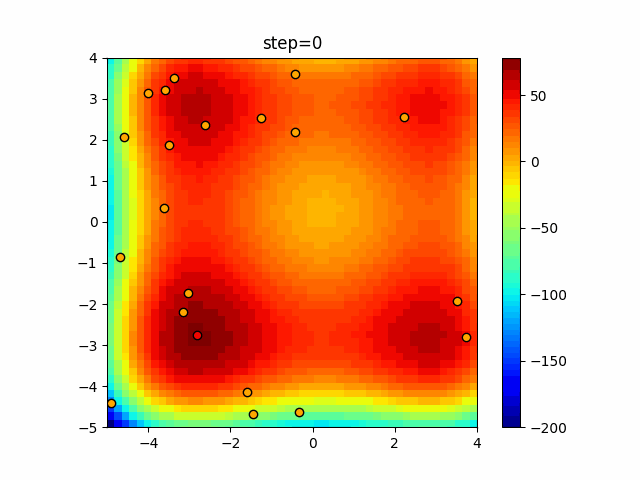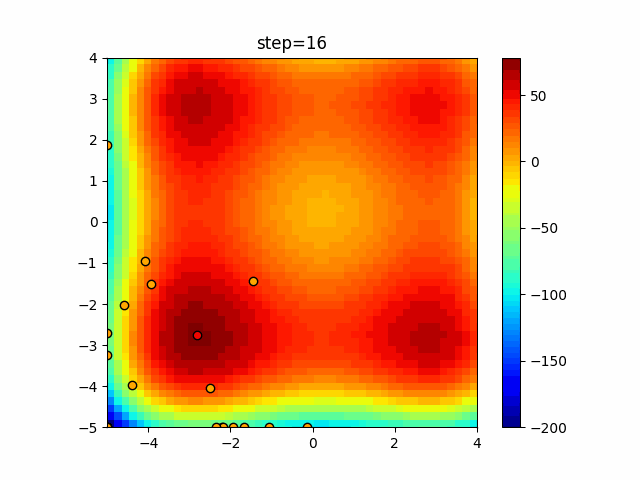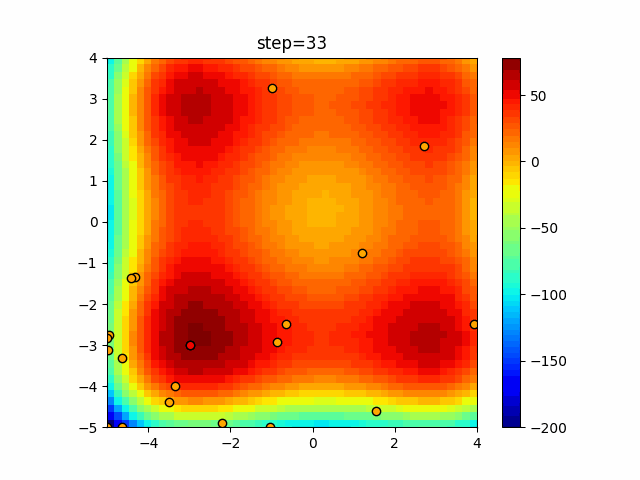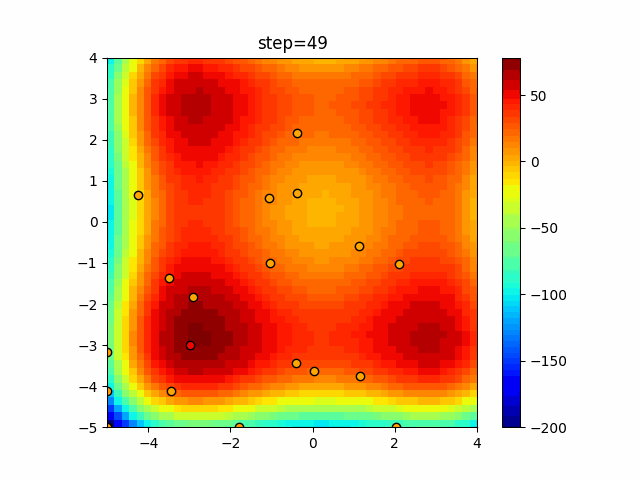
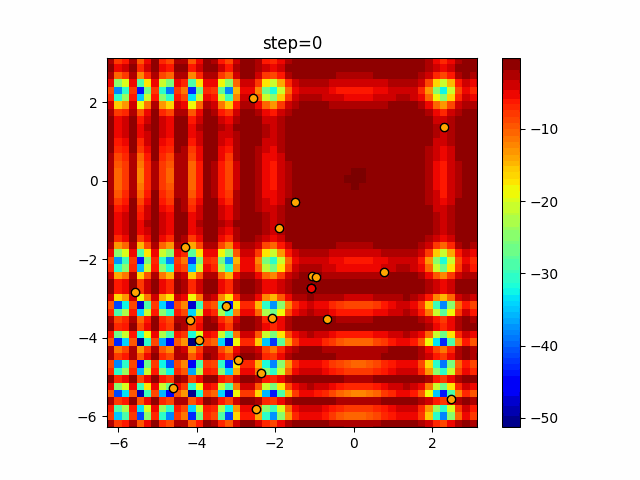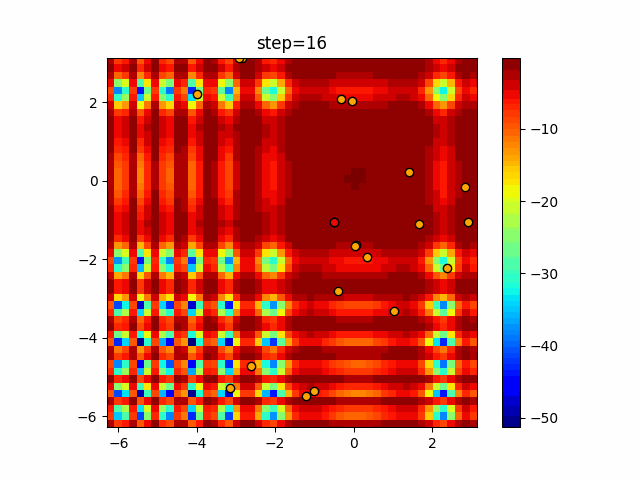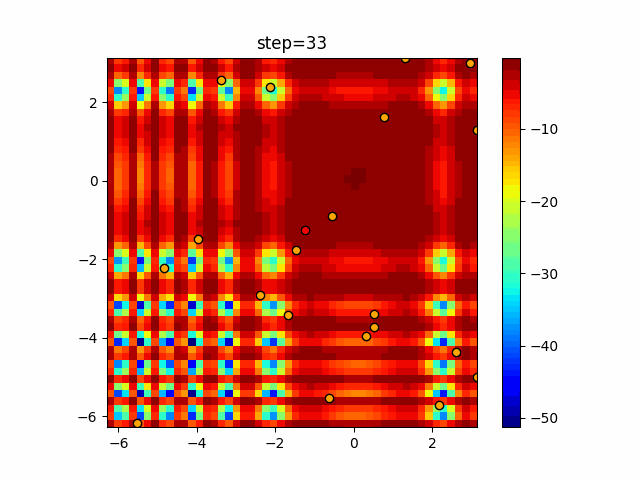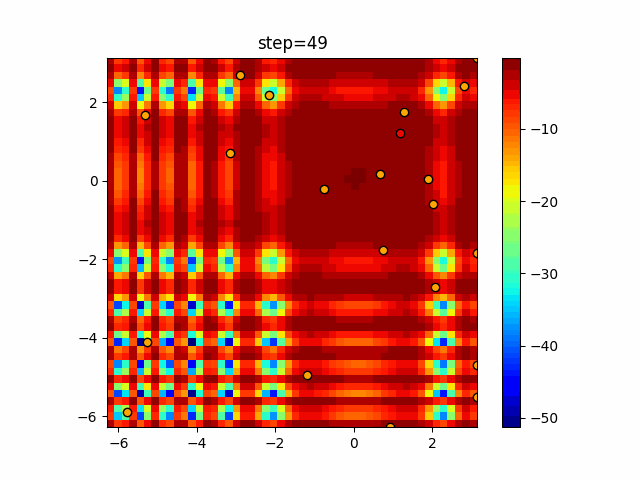
Visualization of actual movement
The 1st dimension is 6 individuals, and the 2nd dimension is 20 individuals, which is the result of 50 steps. The red circle is the individual with the highest score in that step.
The parameters were executed below.
Bat(N, frequency_min=0, frequency_max=0.05, good_bat_rate=0.1, volume_init=0.5, pulse_convergence_value=0.9, pulse_convergence_speed=0.1)
function_Ackley
- 1D
- 2D
function_Rastrigin
- 1D
- 2D
function_Schwefel
- 1D
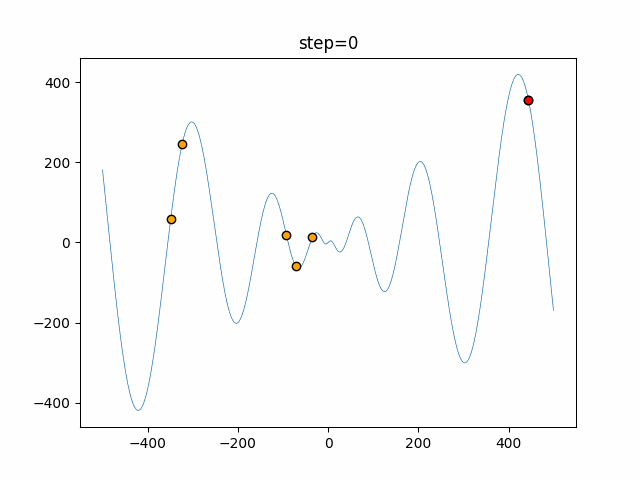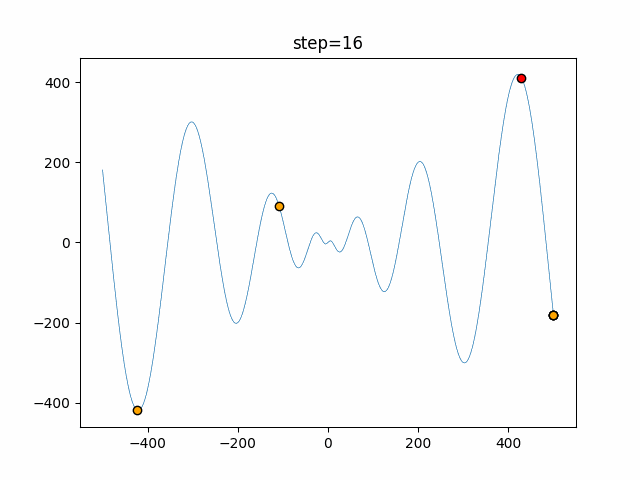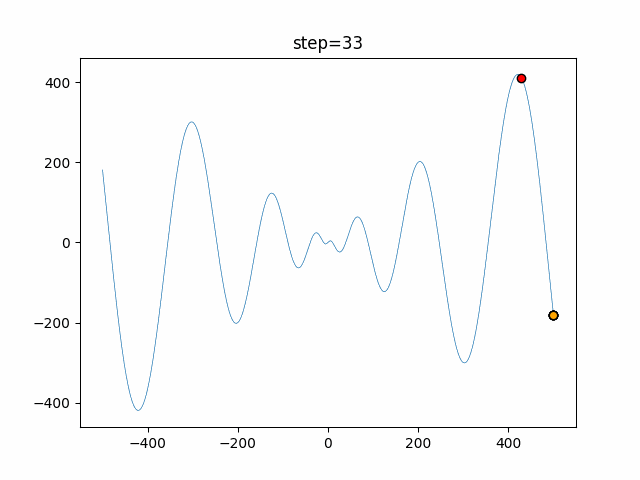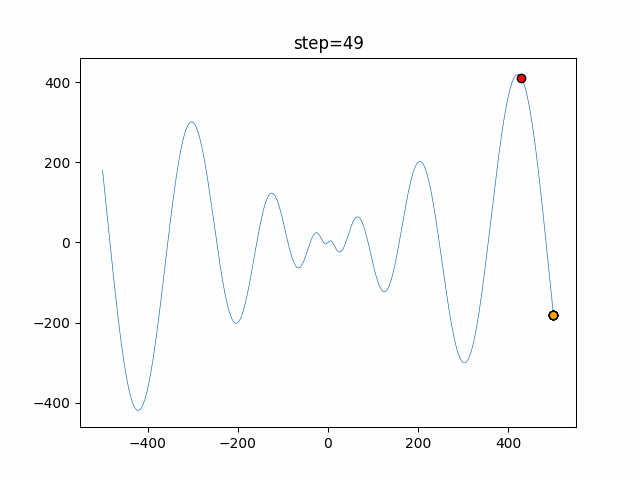
- 2D
function_StyblinskiTang
- 1D
- 2D
function_XinSheYang
- 1D
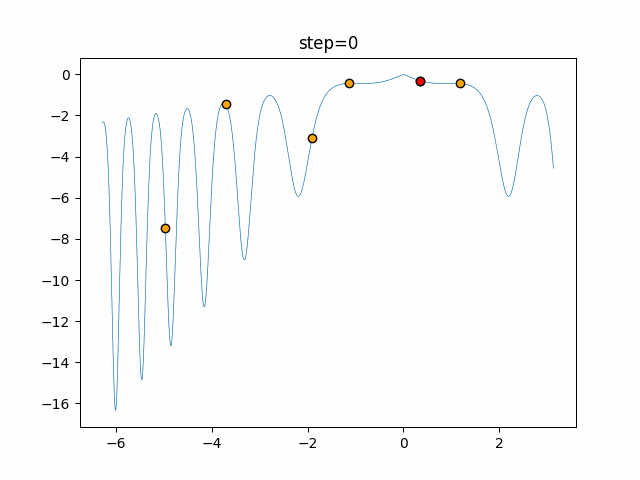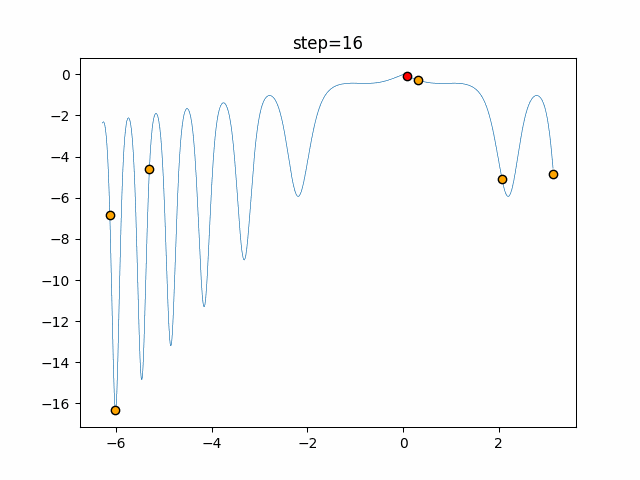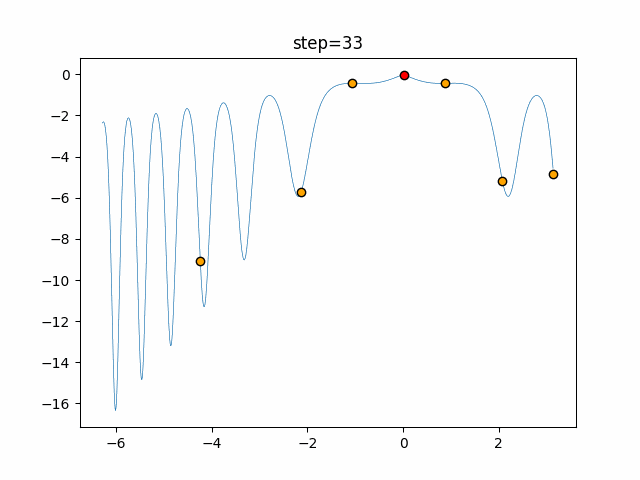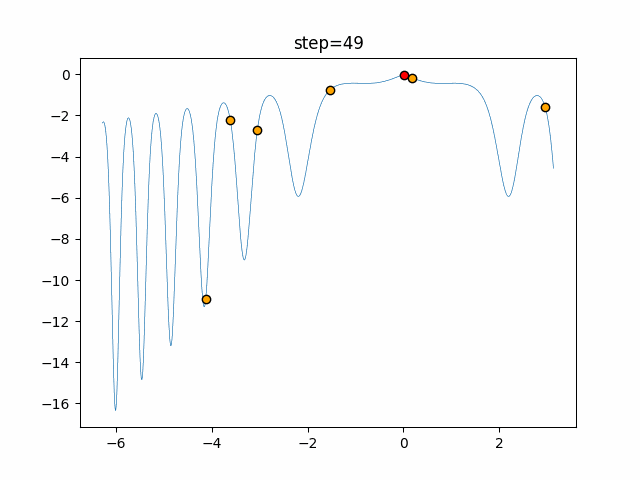
- 2D
Afterword
After moving to the vicinity, the speed remains, so it feels like you are exploring a wide area. Also, since the speed basically remains, it seems that the movement will be very rough in the second half. Adjustment of hyperparameters may be quite severe.
Recommended Posts