We will implement an optimization algorithm (artificial bee colony algorithm)
Introduction
A series of optimization algorithm implementations. First, look at Overview.
The code can be found on github.
Artificial bee colony algorithm
Overview
The Artificial Bee Colony (ABC) is an algorithm based on the foraging behavior of honeybees. Bees feed on nectar from flowers, and after collecting nectar, they convey information such as the quality and direction of the nectar they have acquired to their friends waiting in the nest in a figure eight dance. The waiting bees decide the honey to go to based on the information of this figure 8 dance.
algorithm
We define the foraging behavior of honeybees from honeybees that play three roles: harvesting bees, following bees, and reconnaissance bees.
- Harvesting bees go to one food source to collect nectar and also explore near the food source
- The follow-up drumstick determines the target food source based on the information of the harvested drumstick and collects nectar.
- Reconnaissance bees look for new food sources when the nectar of the food source is obsessed
Harvest bees have a corresponding food source, and the number of harvest bees and food sources is the same.
- Algorithm flow

- Term correspondence
| problem | Artificial bee colony algorithm |
|---|---|
| Array of input values | Food source(flower) |
| Input value | Food source coordinates |
| Evaluation value | 食糧原のEvaluation value |
- Meaning of variables used in code
| Variable name | meaning | Impressions |
|---|---|---|
| problem | Any problem class (see problem section) | |
| harvest_bee | Number of harvested drumsticks | Same as the number of food sources |
| flowers | Arrangement of food sources | |
| flowers[i]["flower"] | i-th food source | |
| flowers[i]["count"] | Number of honeys collected from the i-th food source | |
| follow_bee | Number of following drumsticks | The higher the value, the lower the number of searches around the high evaluation value. |
| visit_max | Maximum amount of nectar that can be obtained from food sources | The larger the number, the more carefully the search, and the larger the number, the wider the area. |
Harvest drumstick phase
In the harvest bee phase, the harvest bee first explores near its food source. Compare the new food source you found by exploring with the current food source, and if the new food source is good, replace it with the current food source and get honey.
The search creates new coordinates from the coordinates of the current food source and uses those coordinates as the new food source. The new coordinate $ \ vec {y} $ uses another food source l to change the kth component of the current food source coordinate with the following formula.
y^i_j = \left\{
\begin{array}{l}
x_j + rand[-1,1] \times ( x^i_j - x^l_j ) \quad j=k \\
x^i_j \qquad (otherwise)
\end{array}
\right.
Where $ k $ and $ l $ are random numbers, and $ rand [-1,1] $ are real random numbers greater than or equal to -1 and less than or equal to 1. A nearby search is expressed by updating only one component of the coordinates.
The code implementation example is below.
#Harvest drumstick phase
for i in range(harvest_bee):
flower = flowers[i]["flower"]
#Explore near food sources
pos = flower.getArray()
k = random.randint(0, len(pos)-1) #Kth component
flower2 = flowers[random.randint(0, len(flowers)-1)]["flower"]
pos2 = flower2.getArray()
pos[k] += (random.random()*2-1) * (pos[k] - pos2[k])
#New food source
new_flower = problem.create(pos)
#Replace if you like
if new_flower.getScore() > flower.getScore():
flowers[i]["flower"] = new_flower
#Record the best food source
if max_flower.getScore() < new_flower.getScore():
max_flower = new_flower
#Increase the number of times you get honey
flowers[i]["count"] += 1
Follow-up drumstick phase
Randomly select a food source and increase the number of honey acquisitions by +1. Although it is said to be random, the food source to be selected varies the probability by the weight of the evaluation value. (Same as the roulette method of the genetic algorithm)
For example, the evaluation value of food sources 1st: 9 Second: 1 If so, the probability that the first will be chosen is 90%, and the probability that the second will be chosen is 10%.
Although it is a calculation method, a simple cumulative sum selection method is implemented.
First of all, the total evaluation value of all food sources is calculated, but if the evaluation value is negative and the minimum value is used as the reference, there is a problem that it cannot be selected. Therefore, when the minimum value is negative, the distance from 0 is calculated as a weight.
import random
def selectFlower(flowers):
#Put the evaluation values of all individuals in the array
weights = [x.getScore() for x in flowers]
w_min = min(weights)
if w_min < 0:
#If the minimum is negative, the reference is 0 → w_change to min →
weights = [ w + (-w_min*2) for w in weights]
#Random numbers are given by the total weight
r = random.random() * sum(weights)
#Look at the weight in order, and if it is less than a random number, that index is applicable
num = 0
for i, weights in enumerate(weights):
num += weight
if r <= num:
return flowers[i]
assert False, "Should not come here"
#Follow-up drumstick phase
for i in range(follow_bee):
flower = selectFlower(flowers)
flower["count"] += 1
Reconnaissance drumstick phase
In the reconnaissance drumstick phase, the food source that has acquired honey a specified number of times (visit_max) is replaced with a new food source. This is equivalent to terminating the search near the food source and searching for a completely different new food source.
Set visit_max large if you want to explore the area around the food source, and set it small if you want to explore a wide area.
#Reconnaissance drumstick phase
for i in range(len(flowers)):
#Replace food sources more than a certain number of times
if visit_max < flowers[i]["count"]:
o = problem.create() #New food source
flowers[i]["count"] = 0
flowers[i]["flower"] = o
#Record the best food source
if max_flower.getScore() < o.getScore():
max_flower = o
Whole code
import math
import random
class ABC():
def __init__(self,
harvest_bee, #Number of harvested drumsticks
follow_bee=10, #Number of following drumsticks
visit_max=10 #Food source(Honey)Maximum number of acquisitions
):
self.harvest_bee = harvest_bee
self.follow_bee = follow_bee
self.visit_max = visit_max
def init(self, problem):
self.problem = problem
self.max_flower = None
self.flowers = []
for _ in range(self.harvest_bee):
#I want to save the number of times the food source is acquired, so I create an additional count variable
o = problem.create()
self.flowers.append({
"flower": o,
"count": 0
})
#Save the largest food source
if self.max_flower is None or self.max_flower.getScore() < o.getScore():
self.max_flower = o
def step(self):
#Harvest drumstick phase
for i in range(self.harvest_bee):
flower = self.flowers[i]["flower"]
#Explore near food sources
pos = flower.getArray()
k = random.randint(0, len(pos)-1) #Randomly decide one ingredient
flower2 = self.flowers[random.randint(0, len(self.flowers)-1)]["flower"]
pos2 = flower2.getArray() #Another food source
pos[k] += (random.random()*2-1) * (pos[k] - pos2[k])
#Create a food source with new coordinates
new_flower = self.problem.create(pos)
#Update if new food source is good
if new_flower.getScore() > flower.getScore():
self.flowers[r]["flower"] = new_flower
#Save the largest food source
if self.max_flower.getScore() < new_flower.getScore():
self.max_flower = new_flower
#Number of acquisitions of food sources+1
self.flowers[r]["count"] += 1
#Follow-up drumstick phase
for i in range(self.follow_bee):
#Randomly selected according to the evaluation value of the food source
index = self._selectFlower()
#Number of acquisitions of food sources+1
self.flowers[index]["count"] += 1
#Reconnaissance drumstick phase
for i in range(len(self.flowers)):
#Replace food sources that have been visited more than a certain number of times
if self.visit_max < self.flowers[i]["count"]:
#Create a new food source
o = self.problem.create()
self.flowers[i]["count"] = 0
self.flowers[i]["flower"] = o
#Save the largest food source
if self.max_flower.getScore() < o.getScore():
self.max_flower = o
def _selectFlower(self):
#Arrange the evaluation values of all food sources
weights = [x["flower"].getScore() for x in self.flowers]
w_min = min(weights)
if w_min < 0:
#If the minimum is negative, the reference is 0 → w_change to min →
weights = [ w + (-w_min*2) for w in weights]
#Random numbers are given by the total weight
r = random.random() * sum(weights)
#Look at the weight in order, and if it is less than a random number, that index is applicable
num = 0
for i, weights in enumerate(weights):
num += weight
if r <= num:
return i
raise ValueError()
Hyperparameter example
It is the result of optimizing hyperparameters with optuna for each problem. A single optimization attempt yields results with a search time of 2 seconds. I did this 100 times and asked optuna to find the best hyperparameters.
| problem | follow_bee | harvest_bee | visit_max |
|---|---|---|---|
| EightQueen | 1 | 47 | 84 |
| function_Ackley | 1 | 24 | 77 |
| function_Griewank | 4 | 24 | 100 |
| function_Michalewicz | 4 | 32 | 100 |
| function_Rastrigin | 1 | 50 | 89 |
| function_Schwefel | 6 | 44 | 99 |
| function_StyblinskiTang | 1 | 18 | 96 |
| LifeGame | 4 | 38 | 10 |
| OneMax | 34 | 37 | 19 |
| TSP | 3 | 38 | 94 |
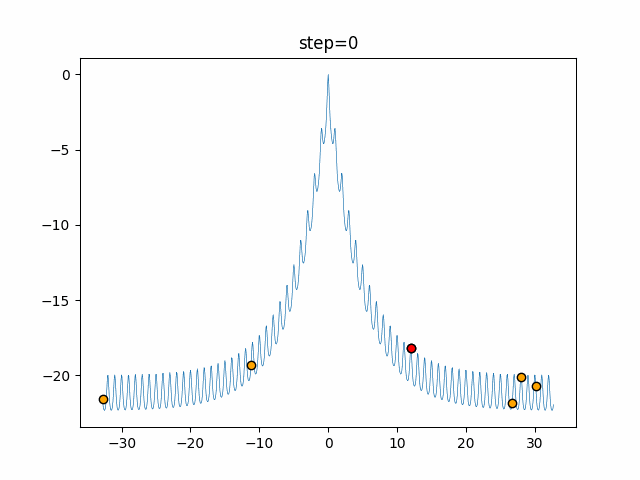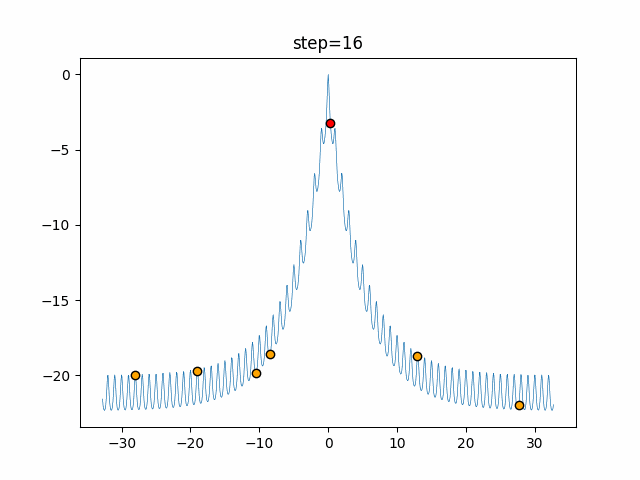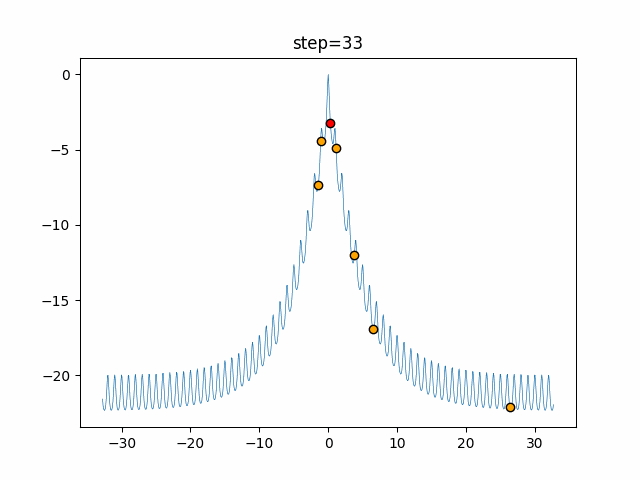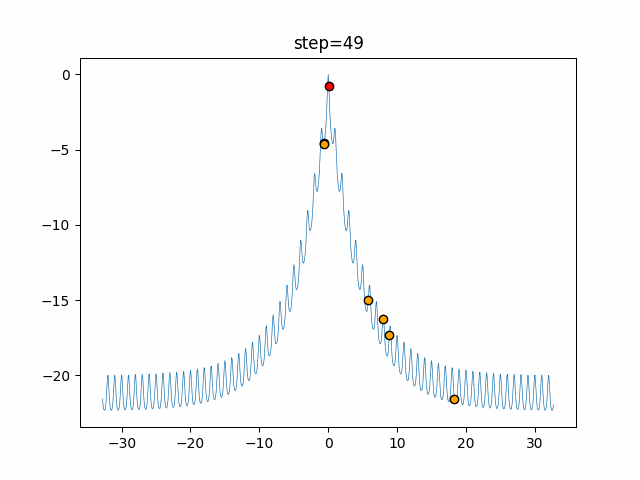
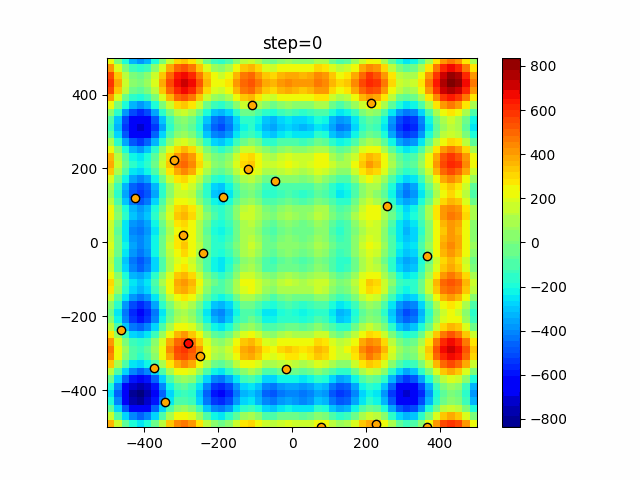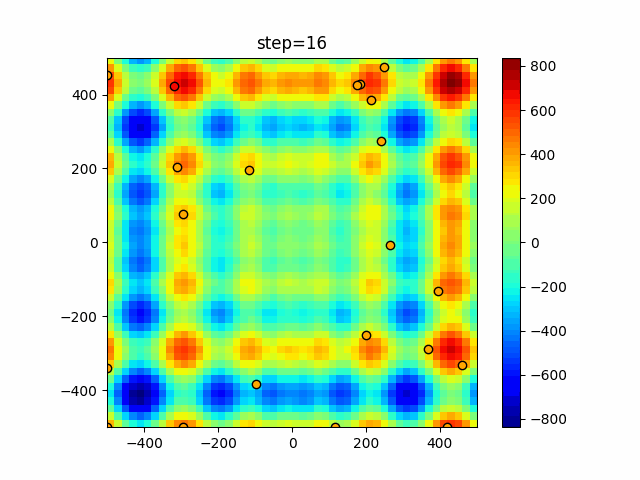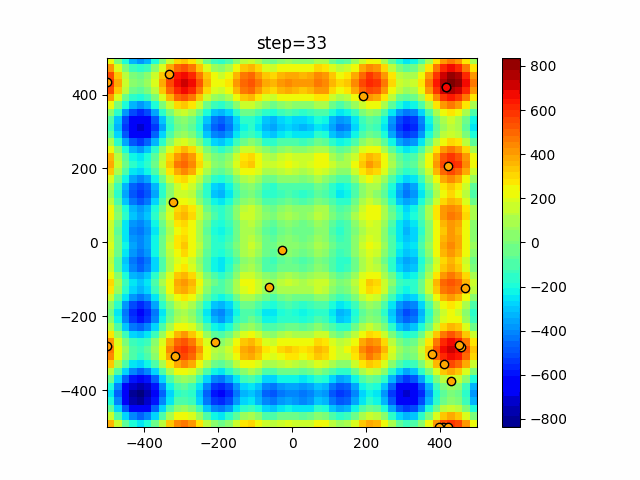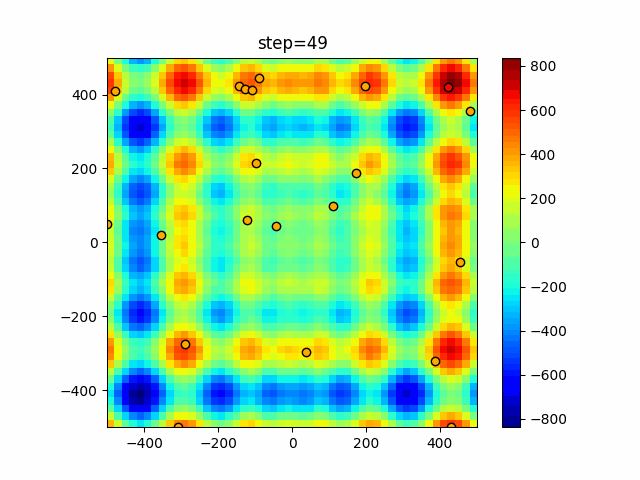
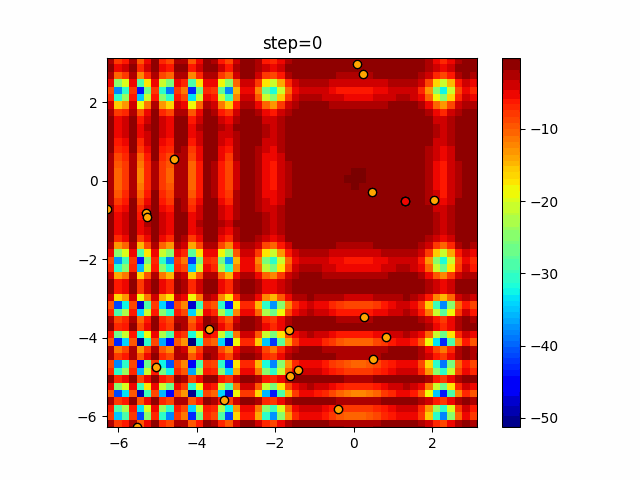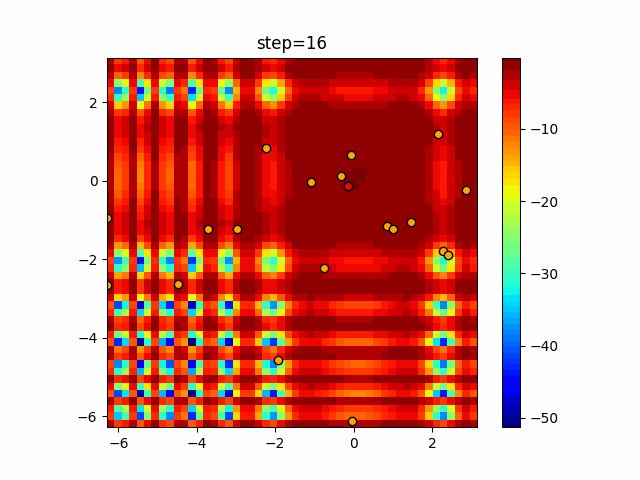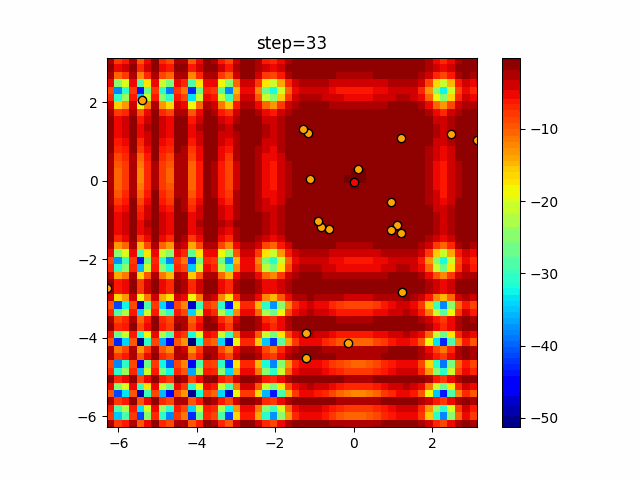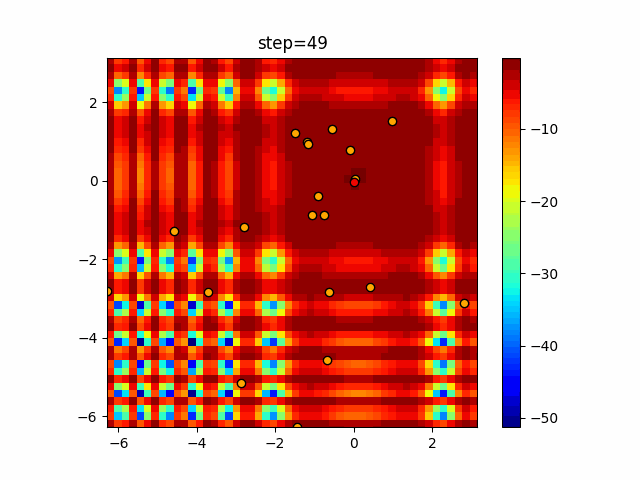
Visualization of actual movement
The 1st dimension is 6 individuals, and the 2nd dimension is 20 individuals, which is the result of 50 steps. The red circle is the individual with the highest score in that step.
The parameters were executed below.
ABC(N, follow_bee=15, visit_max=30)
function_Ackley
- 1D
- 2D

function_Rastrigin
- 1D
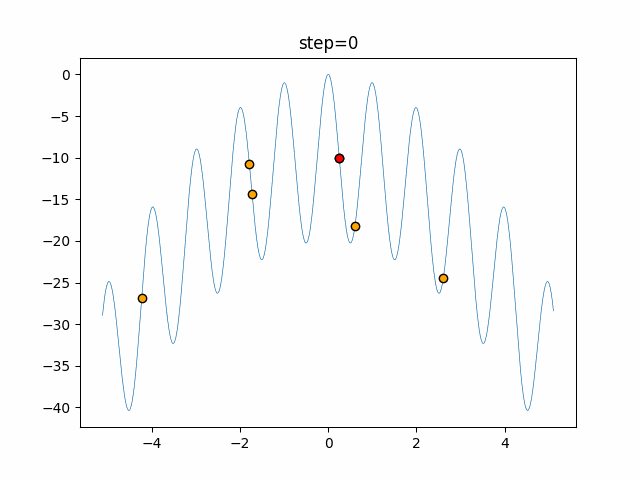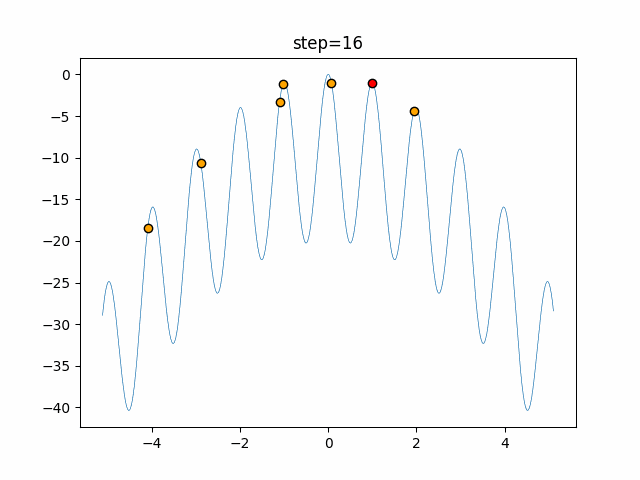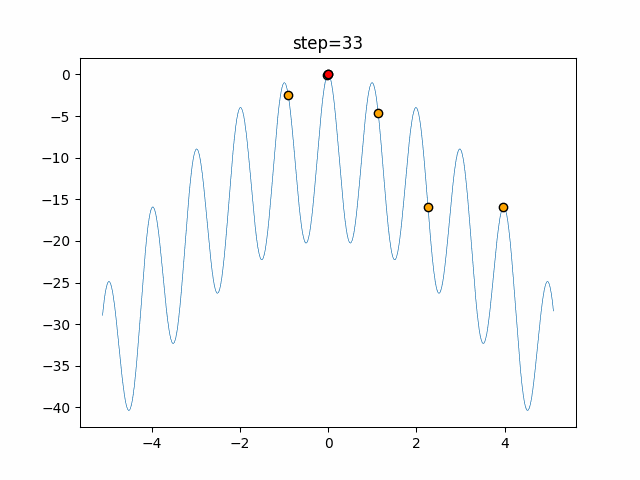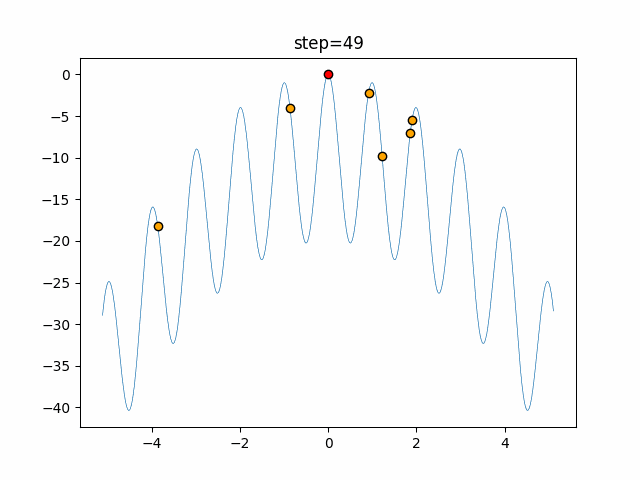
- 2D
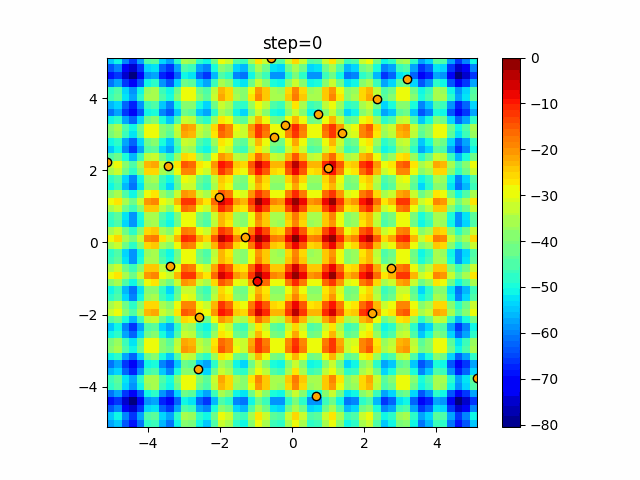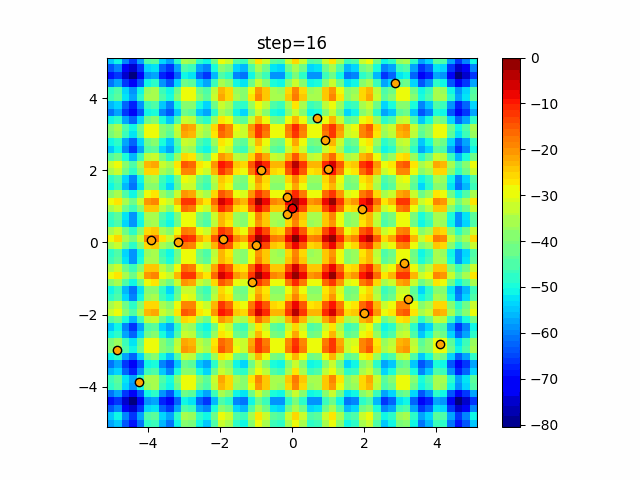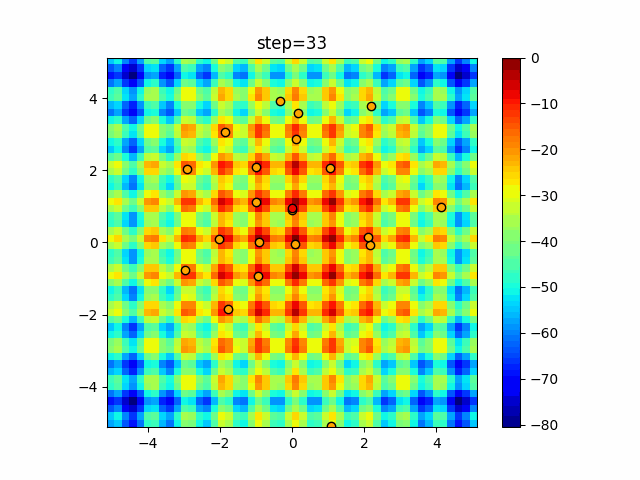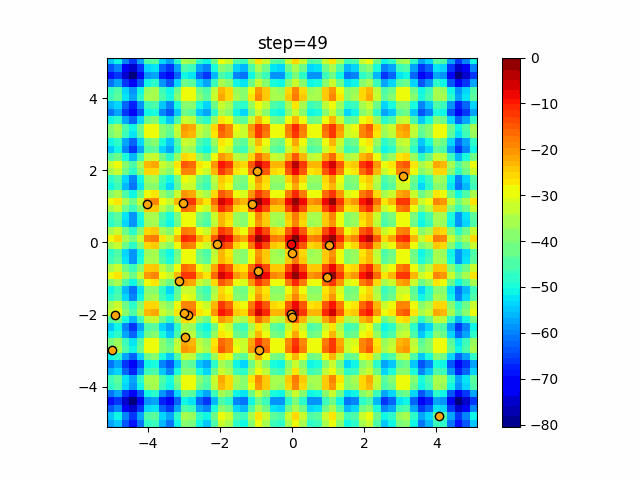
function_Schwefel
- 1D
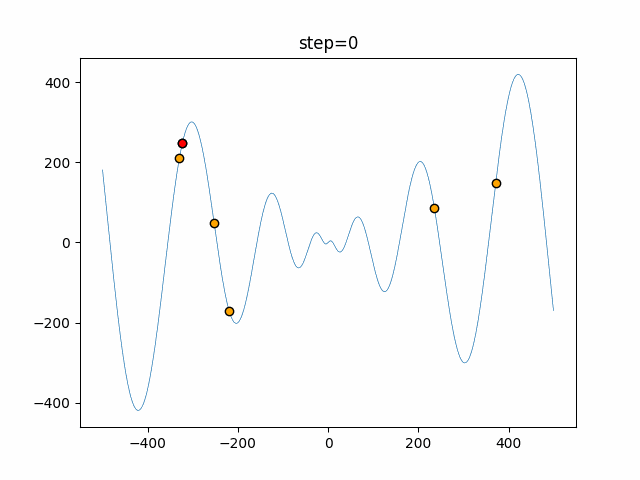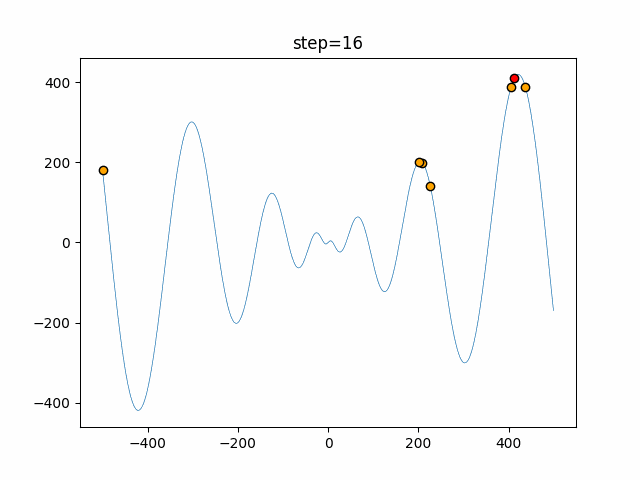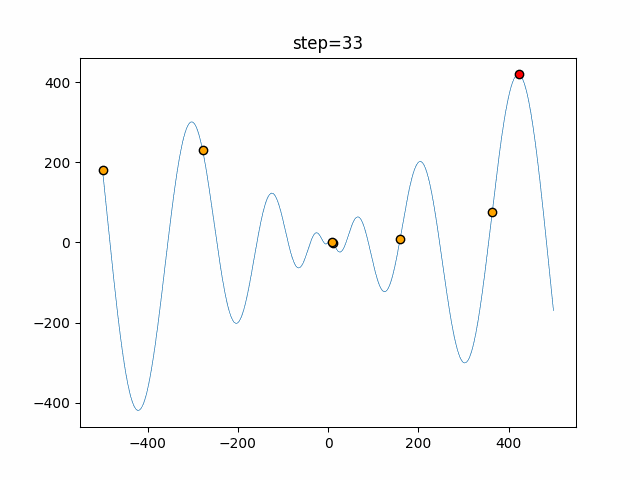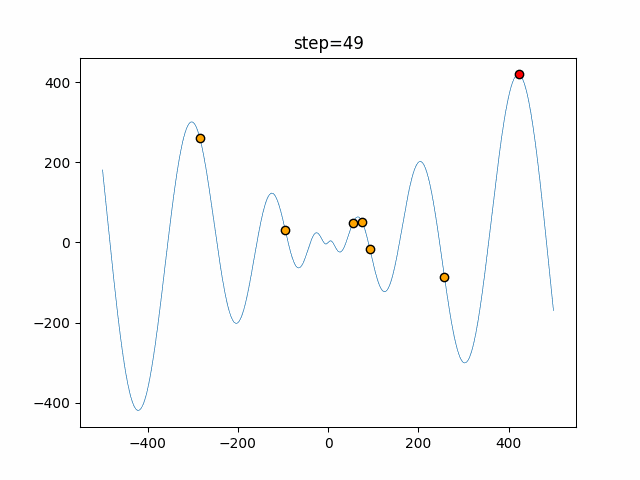
- 2D
function_StyblinskiTang
- 1D
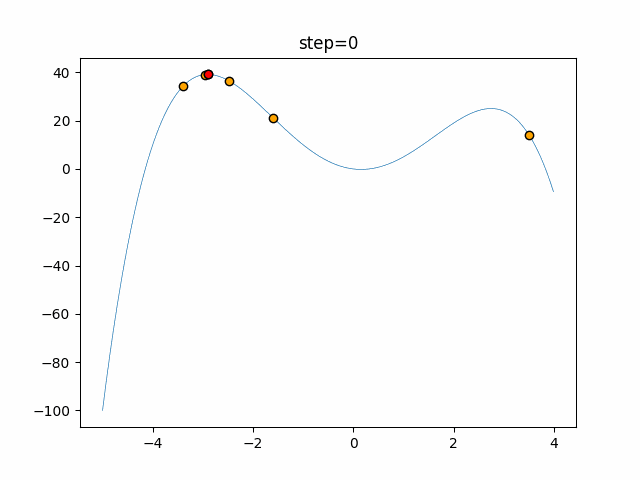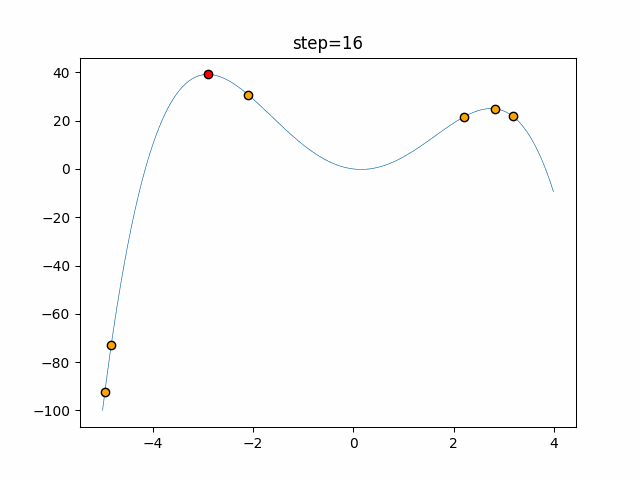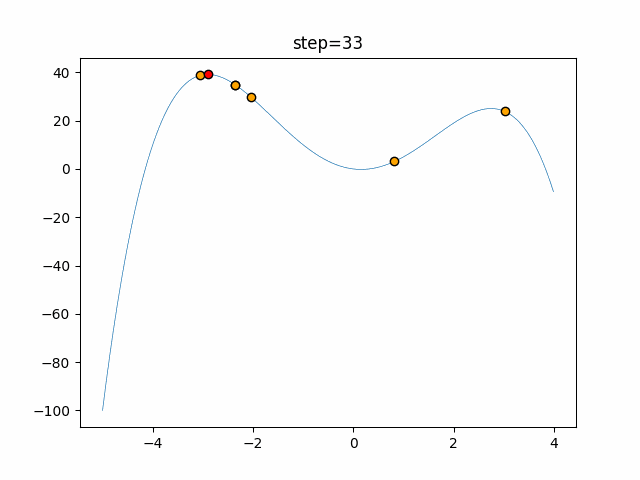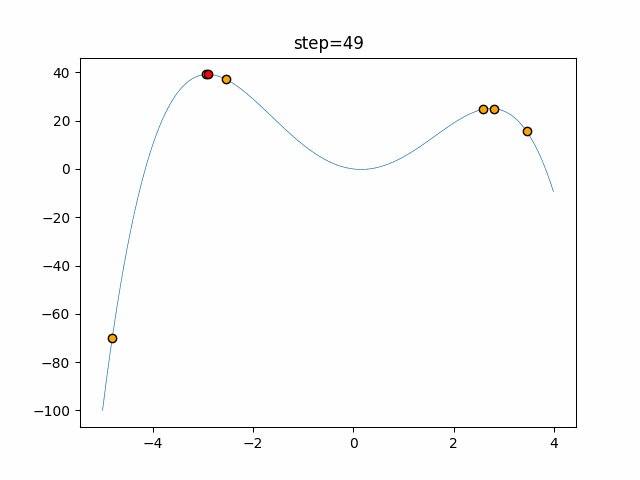
- 2D
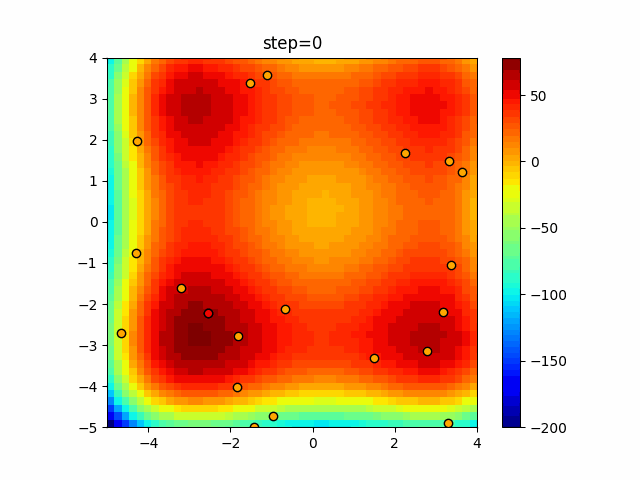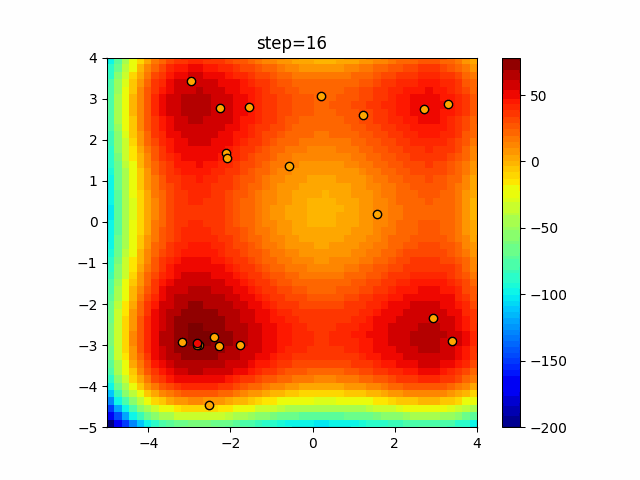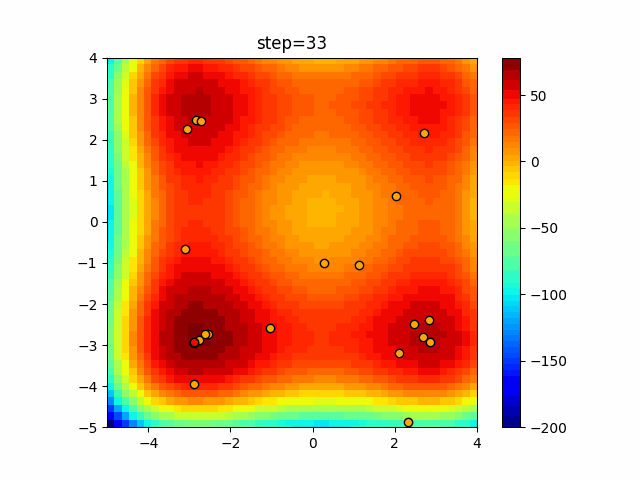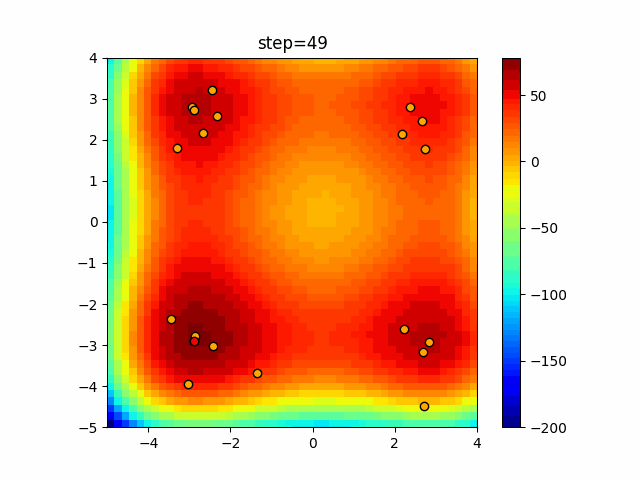
function_XinSheYang
- 1D
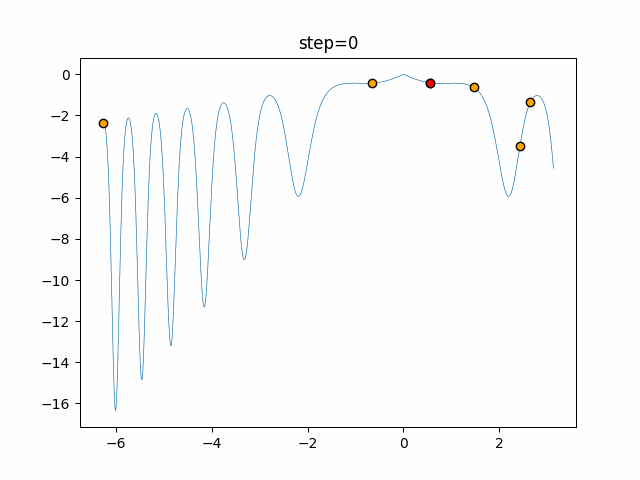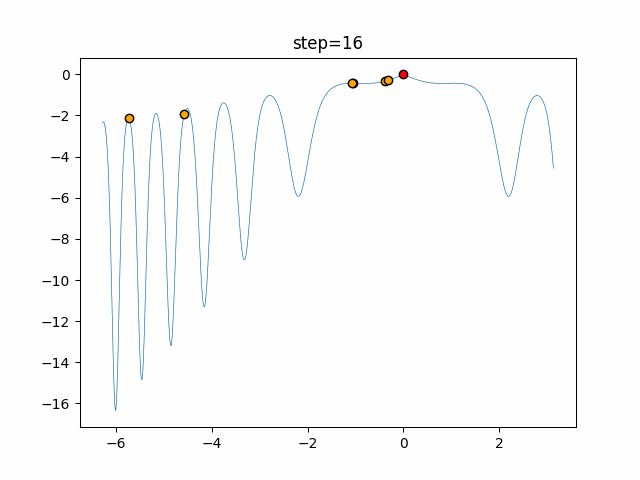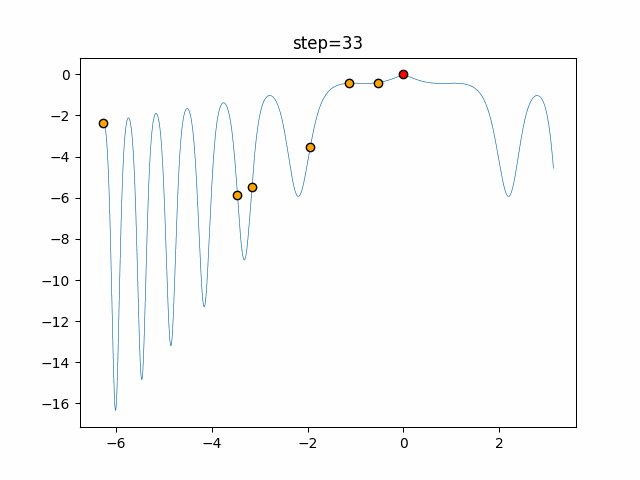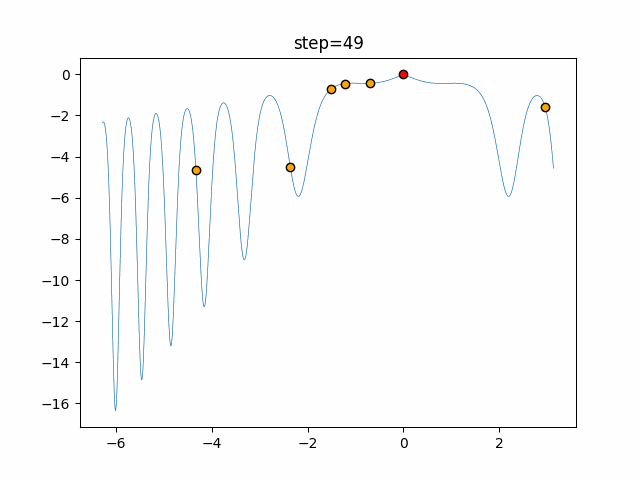
- 2D
Afterword
It is unlikely that you will fall into a local solution because it repeats searching near and moving far away. It seems difficult to determine the parameters for the follow-up drumstick and the number of visits, but it seems that good results will be achieved if it can be adjusted in a good way.
Recommended Posts