We will implement an optimization algorithm (genetic algorithm)
Introduction
A series of optimization algorithm implementations. First, look at Overview.
The code can be found on github.
Genetic algorithm
Overview
The Genetic Algorithm (GA) is an algorithm created based on the evolution of genes.
algorithm
As a flow, the following is repeated for each generation (step).
- Selection of parent individual (priority is given to individuals with high fitness)
- Generate a child individual based on the parent individual
- Change the parent generation to the child generation when the number of offspring exceeds a certain level
The characteristic of generating offspring is to generate an individual that inherits the characteristics of a parent individual called crossover.
- Algorithm flow

- Term correspondence
| problem | Genetic algorithm |
|---|---|
| Array of input values | individual |
| Input value | (Individual has)gene |
| Evaluation value | Fitness of an individual to the environment |
- About variables in code
| Variable name | meaning | Impressions |
|---|---|---|
| problem | Any problem class (see problem section) | |
| individual_max | Population | |
| mutation | Mutation probability | The larger the value, the more random searches |
Selection of parent individual
Select two individuals from all individuals. There are several ways to choose, but we have implemented a roulette method and a ranking method.
Also, for ease of implementation, we do not consider duplication of the two individuals. (So the same individual may be selected)
Roulette method
This is a selection method in which the higher the evaluation value of an individual, the higher the probability of being selected. For example, the evaluation value of an individual 1st: 9 Second: 1 If so, the probability that the first will be chosen is 90%, and the probability that the second will be chosen is 10%.
The calculation method implements a simple cumulative sum selection method.
When the evaluation value is negative, there is a problem that the minimum value is not selected in the cumulative sum, so If the minimum value is negative, the distance from 0 is calculated as a weight.
The code implementation example is below.
import random
def selectRoulette(individuals):
#individuals represent the sequence of each individual.
#Put the evaluation values of all individuals in the array
weights = [x.getScore() for x in individuals]
w_min = min(weights)
if w_min < 0:
#If the minimum is negative, the reference is 0 → w_change to min →
weights = [ w + (-w_min*2) for w in weights]
#Random numbers are given by the total weight
r = random.random() * sum(weights)
#Look at the weight in order, and if it is less than a random number, that index is applicable
num = 0
for i, weights in enumerate(weights):
num += weight
if r <= num:
return individuals[i]
assert False, "Should not come here"
Ranking method
It is a method to select based on the ranking of the evaluation value of the individual. For example, the evaluation value of an individual 1st: 9 (1st place) 2nd: 1 (2nd place) In that case, the probability that the first one will be selected is (2/3) = 66.7%, and the probability that the second one will be selected is 33.3%.
The calculation method is Inverse Transform Method.
The code implementation example is below.
import math
import random
#Sum of arithmetic progressions
def arithmetic_sequence_sum(size, start=1, diff=1):
return size*( 2*start + (size-1)*diff )/2
#Inverse function of sum of arithmetic progression
def arithmetic_sequence_sum_inverse(val, start=1, diff=1):
if diff == 0:
return val
t = diff-2*start + math.sqrt((2*start-diff)**2 + 8*diff*val)
return t/(2*diff)
def selectRanking(individuals):
#Sort by rank
#0 is the lowest and len(individuals)-1 is 1st
individuals.sort(key=lambda x: x.getScore())
#Number of individuals
size = len(individuals)
#Get the total value of all ranks
num = arithmetic_sequence_sum(size)
#Random numbers are given from the total value
r = random.random() * num
#Find the rank with the inverse function
index = int(arithmetic_sequence_sum_inverse(r))
return individuals[index]
Crossing
In crossover, two new individuals (child individuals) are generated from two individuals (parent individuals). There are various types of crossovers, but we emphasize versatility and implement only uniform crossovers.
Uniform crossing is an operation such as replacing the parent gene with a 50% probability for the individual gene.
In addition, each gene is mutated (does not inherit the genetic information of the parent) with an arbitrary probability.
The code implementation example is below.
import math
import random
def cross(parent1, parent2):
problem =Any problem class (see problem section)
mutation = 0.1 #Mutation probability
genes1 = parent1.getArray() #Genetic information of parent 1
genes2 = parent2.getArray() #Genetic information of parent 2
#Genetic information of the child
c_genes1 = []
c_genes2 = []
for i in range(len(genes1)): #Scan each gene
# 50%Swap genes with a probability of
if random.random() < 0.5:
c_gene1 = genes1[i]
c_gene2 = genes2[i]
else:
c_gene1 = genes2[i]
c_gene2 = genes1[i]
#mutation
if random.random() < mutation:
c_gene1 = problem.randomVal() #Make it a random value
if random.random() < mutation:
c_gene2 = problem.randomVal() #Make it a random value
c_genes1.append(c_gene1)
c_genes2.append(c_gene2)
#Generate a child based on a gene
childe1 = problem.create(c_genes1)
childe2 = problem.create(c_genes2)
return childe1, childe2
Other
Elite strategy
Regarding the generation of children for the next generation, the elite strategy is to carry over the parent individual, which has the highest evaluation in the parent generation, to the next generation as it is. Since the elite remains, the decrease in the optimal solution due to crossover can be prevented, but since many elite genes remain, it may be difficult to escape from the local solution (diversity is lost).
Whole code
import math
import random
#Sum of arithmetic progressions
def arithmetic_sequence_sum(size, start=1, diff=1):
return size*( 2*start + (size-1)*diff )/2
#Inverse function of sum of arithmetic progression
def arithmetic_sequence_sum_inverse(val, start=1, diff=1):
if diff == 0:
return val
t = diff-2*start + math.sqrt((2*start-diff)**2 + 8*diff*val)
return t/(2*diff)
class GA():
def __init__(self,
individual_max, #Population
save_elite=True, #Whether to keep the elite alive
select_method="ranking", #Selection method(roulette or ranking)
mutation=0.1, #Mutation probability
):
self.individual_max = individual_max
self.save_elite = save_elite
self.select_method = select_method
self.mutation = mutation
def init(self, problem):
self.problem = problem
#Generate each individual.
self.best_individual = None
self.individuals = []
for _ in range(self.individual_max):
o = problem.create()
self.individuals.append(o)
#Save the highest rated individual
if self.best_individual is None or self.best_individual.getScore() < o.getScore():
self.best_individual = o
#Sort by fitness
self.individuals.sort(key=lambda x: x.getScore())
def step(self):
#Next generation
next_individuals = []
if self.save_elite:
#Survive the elite
next_individuals.append(self.individuals[-1].copy())
for _ in range(self.individual_max): #while is fine, but for safety
#Repeat until the number is collected
if len(next_individuals) > self.individual_max:
break
#select
if self.select_method == "roulette":
o1 = self._selectRoulette()
o2 = self._selectRoulette()
elif self.select_method == "ranking":
o1 = self._selectRanking()
o2 = self._selectRanking()
else:
raise ValueError()
#Cross
new_o1, new_o2 = self._cross(o1, o2)
#Added to the next generation
next_individuals.append(new_o1)
next_individuals.append(new_o2)
#Alternation of generations
self.individuals = next_individuals
#Sort by fitness
self.individuals.sort(key=lambda x: x.getScore())
#Save the highest rating
if self.best_individual.getScore() < self.individuals[-1].getScore():
self.best_individual = self.individuals[-1]
def _selectRoulette(self):
#Put the evaluation values of all individuals in the array
weights = [x.getScore() for x in self.individuals]
w_min = min(weights)
if w_min < 0:
#If the minimum is negative, the reference is 0 → w_change to min →
weights = [ w + (-w_min*2) for w in weights]
#Random numbers are given by the total weight
r = random.random() * sum(weights)
#Look at the weight in order, and if it is less than a random number, that index is applicable
num = 0
for i, weights in enumerate(weights):
num += weight
if r <= num:
return self.individuals[i]
raise ValueError()
def _selectRanking(self):
#Number of individuals
size = len(self.individuals)
#Get the total value of all ranks
num = arithmetic_sequence_sum(size)
#Random numbers are given from the total value
r = random.random() * num
#Find the rank with the inverse function
index = int(arithmetic_sequence_sum_inverse(r))
return self.individuals[index]
def _cross(self, parent1, parent2):
genes1 = parent1.getArray() #Genetic information of parent 1
genes2 = parent2.getArray() #Genetic information of parent 2
#Genetic information of the child
c_genes1 = []
c_genes2 = []
for i in range(len(genes1)): #Scan each gene
# 50%Swap genes with a probability of
if random.random() < 0.5:
c_gene1 = genes1[i]
c_gene2 = genes2[i]
else:
c_gene1 = genes2[i]
c_gene2 = genes1[i]
#mutation
if random.random() < self.mutation:
c_gene1 = self.problem.randomVal()
if random.random() < self.mutation:
c_gene2 = self.problem.randomVal()
c_genes1.append(c_gene1)
c_genes2.append(c_gene2)
#Generate a child based on a gene
childe1 = self.problem.create(c_genes1)
childe2 = self.problem.create(c_genes2)
return childe1, childe2
Parameter-free GA (PfGA)
It is a GA found on the reference site that does not require parameter setting. It looks interesting, so I implemented it.
Reference: Parameter-free GA (PfGA)
It is basically the same as GA, but GA is performed without limiting the number of individuals by using a group (local group) that collects individuals.
- Algorithm flow

Local population
The local population first contains two individuals. After that, two bodies are randomly taken out from the local population and crossed with the two bodies to make two offspring. After that, the evaluation values of the four individuals are returned to the local population under the following conditions.
- If both of the two offspring are better than the two parents, the two offspring and the three parents with better fitness will return to the local population and the number of local populations will increase by one.
- If both of the two offspring are worse than the two parents, only the better of the two parents will return to the local population and the number of local populations will decrease by one.
- If only one of the two parents is better than the two offspring, the better of the two parents and the better of the two offspring will return to the local population and the number of local populations will not change. ..
- If only one of the two offspring is better than the two parents, only the better of the two offspring will return to the local population, randomly selecting one from the entire search space and adding it to the local population. To do. The number of local populations does not change.
Whole code
The whole code. However, although it is said to be parameter-free, the probability of mutation seems to be set.
import math
import random
class PfGA():
def __init__(self, mutation=0.1):
self.mutation = mutation #Mutation probability
def init(self, problem):
self.problem = problem
#First two bodies are generated
self.individuals = [] #Local population(local individuals)
for _ in range(2):
self.individuals.append(problem.create())
def step(self):
#Add if less than 2
if len(self.individuals) < 2:
self.individuals.append(self.problem.create())
#Take out 2 at random
p1 = self.individuals.pop(random.randint(0, len(self.individuals)-1))
p2 = self.individuals.pop(random.randint(0, len(self.individuals)-1))
#Create a child
c1, c2 = self._cross(p1, p2)
if p1.getScore() < p2.getScore():
p_min = p1
p_max = p2
else:
p_min = p2
p_max = p1
if c1.getScore() < c2.getScore():
c_min = c1
c_max = c2
else:
c_min = c2
c_max = c1
if c_min.getScore() >= p_max.getScore():
#When both two offspring are better than the two parents
#Two offspring and a total of three parents with good fitness return to the local population, and the number of local populations increases by one.
self.individuals.append(c1)
self.individuals.append(c2)
self.individuals.append(p_max)
elif p_min.getScore() >= c_max.getScore():
#When both two offspring are worse than the two parents
#Only the better of the two parents returns to the local population, and the number of local populations decreases by 1.
self.individuals.append(p_max)
elif p_max.getScore() >= c_max.getScore() and p_min.getScore() <= c_max.getScore():
#When only one of the two parents is better than the two children
#The better of the two parents and the better of the two children return to the local population, and the number of local populations does not change.
self.individuals.append(c_max)
self.individuals.append(p_max)
elif c_max.getScore() >= p_max.getScore() and c_min.getScore() <= p_max.getScore():
#When only one of the two offspring is better than the two parents
#Only the better of the two offspring will return to the local population, and one will be randomly selected from the entire search space and added to the local population. The number of local populations does not change.
self.individuals.append(c_max)
self.individuals.append(self.problem.create())
else:
raise ValueError("not comming")
def _cross(self, parent1, parent2):
genes1 = parent1.getArray() #Genetic information of parent 1
genes2 = parent2.getArray() #Genetic information of parent 2
#Genetic information of the child
c_genes1 = []
c_genes2 = []
for i in range(len(genes1)): #Scan each gene
# 50%Swap genes with a probability of
if random.random() < 0.5:
c_gene1 = genes1[i]
c_gene2 = genes2[i]
else:
c_gene1 = genes2[i]
c_gene2 = genes1[i]
#mutation
if random.random() < self.mutation:
c_gene1 = self.problem.randomVal()
if random.random() < self.mutation:
c_gene2 = self.problem.randomVal()
c_genes1.append(c_gene1)
c_genes2.append(c_gene2)
#Generate a child based on a gene
childe1 = self.problem.create(c_genes1)
childe2 = self.problem.create(c_genes2)
return childe1, childe2
Hyperparameter example
It is the result of optimizing hyperparameters with optuna for each problem. One optimization trial yields results with a search time of 2 seconds. I did this 100 times and asked optuna to find the best hyperparameters.
- GA
| problem | individual_max | mutation | save_elite | select_method |
|---|---|---|---|---|
| EightQueen | 4 | 0.013873130609831266 | True | roulette |
| function_Ackley | 9 | 0.018218488205681442 | True | ranking |
| function_Griewank | 26 | 0.009297248466797036 | True | ranking |
| function_Michalewicz | 46 | 0.02028018029181716 | False | ranking |
| function_Rastrigin | 49 | 0.00831170762967785 | True | ranking |
| function_Schwefel | 11 | 0.015576469028724699 | True | ranking |
| function_StyblinskiTang | 37 | 0.01095031028776784 | False | ranking |
| LifeGame | 12 | 0.5516471161744092 | False | ranking |
| OneMax | 2 | 0.020901412496510563 | True | ranking |
| TSP | 24 | 0.010664979238406223 | True | ranking |
- PfGA
| problem | mutation |
|---|---|
| EightQueen | 0.03456922411806109 |
| function_Ackley | 0.011966812535822609 |
| function_Griewank | 0.023555766863728234 |
| function_Michalewicz | 0.021882782991433425 |
| function_Rastrigin | 0.011938744186117622 |
| function_Schwefel | 0.014015707940510776 |
| function_StyblinskiTang | 0.020297589468369463 |
| LifeGame | 0.7819203713430501 |
| OneMax | 0.0008382068017285835 |
| TSP | 0.012371041873054364 |
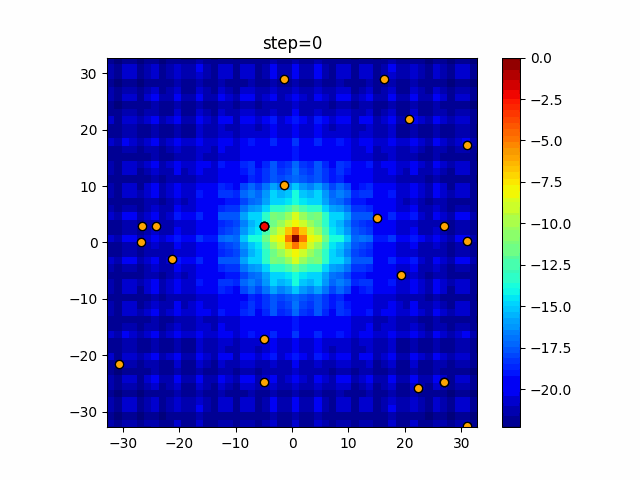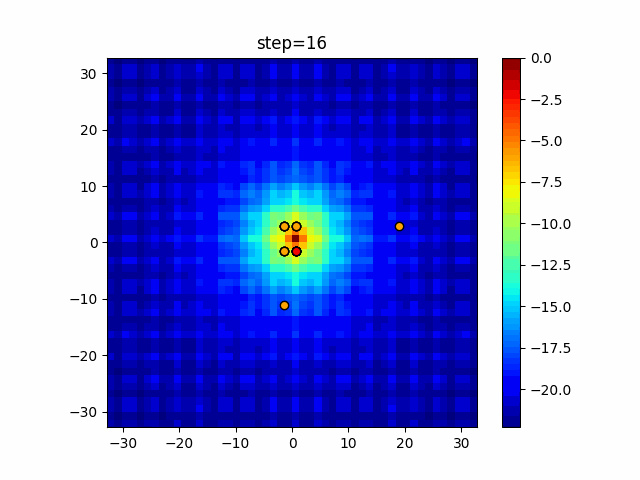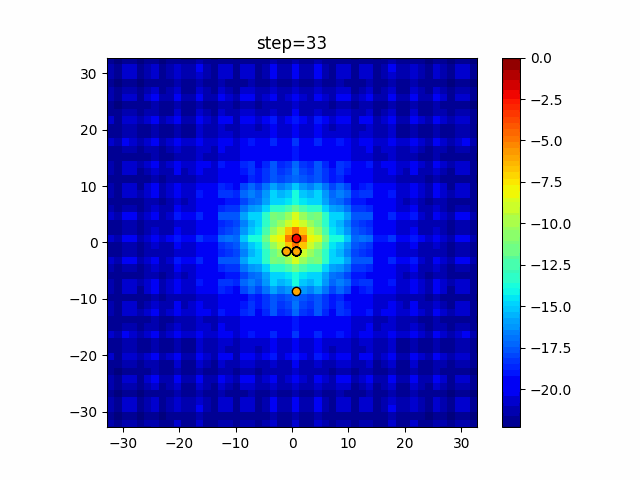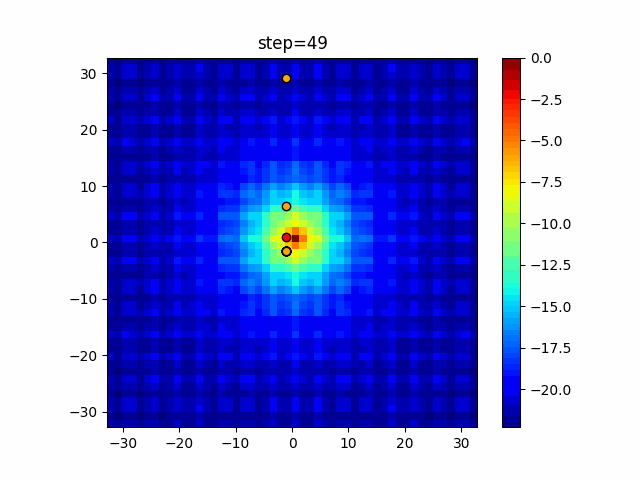
Visualization of actual movement
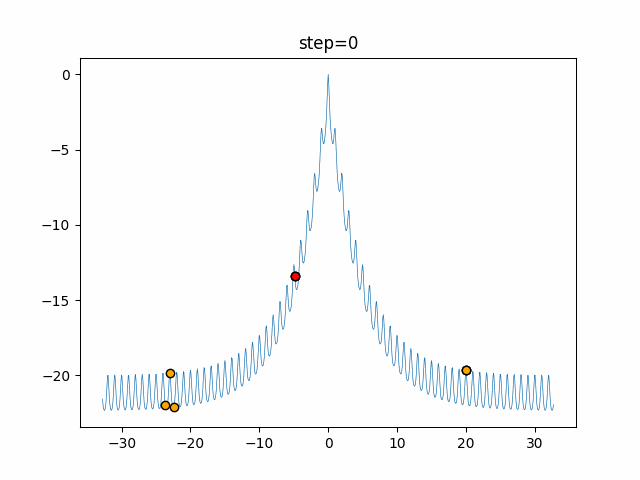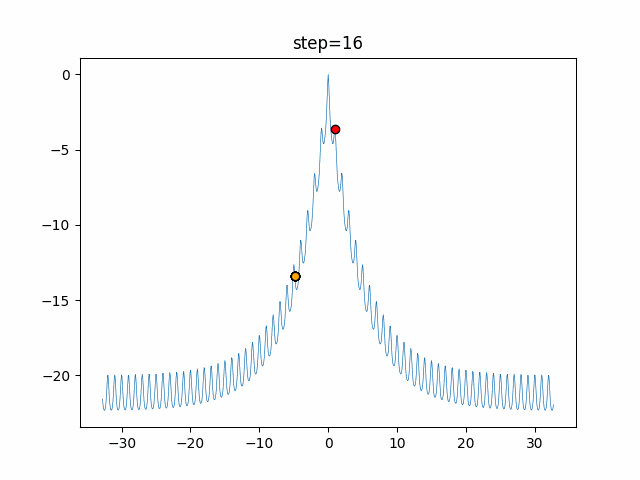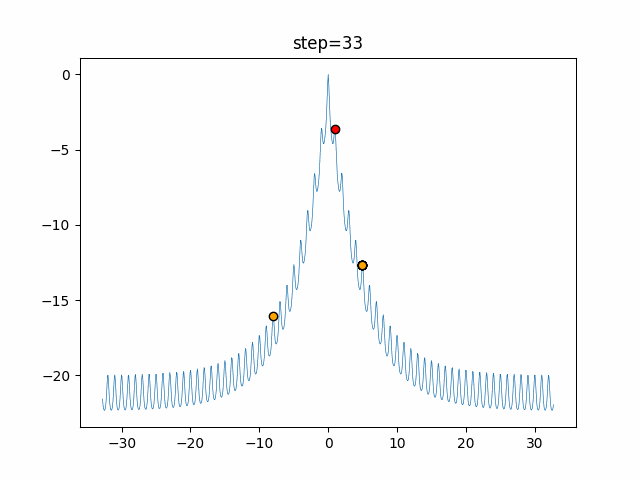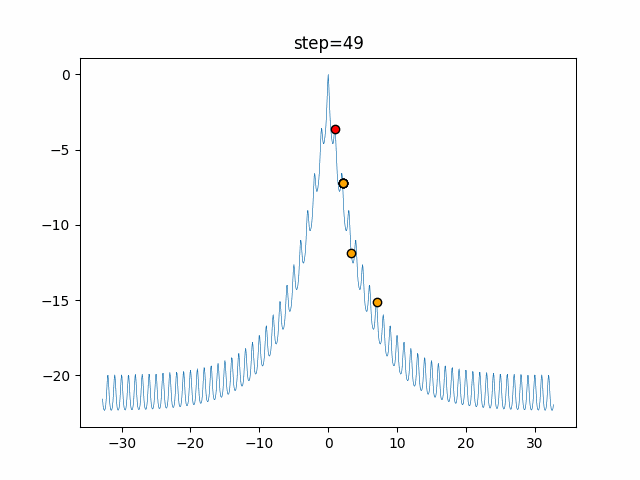
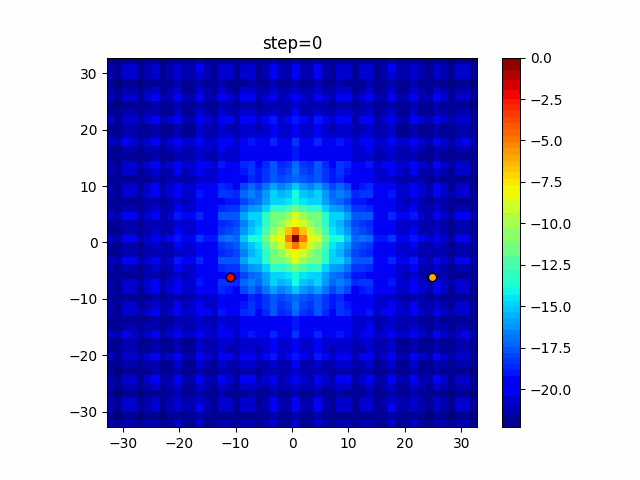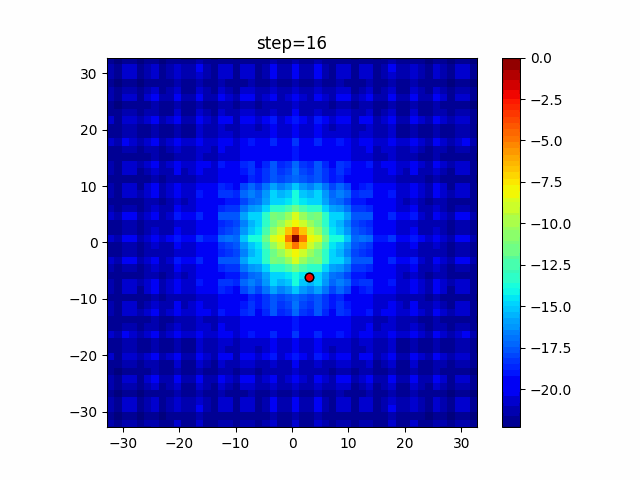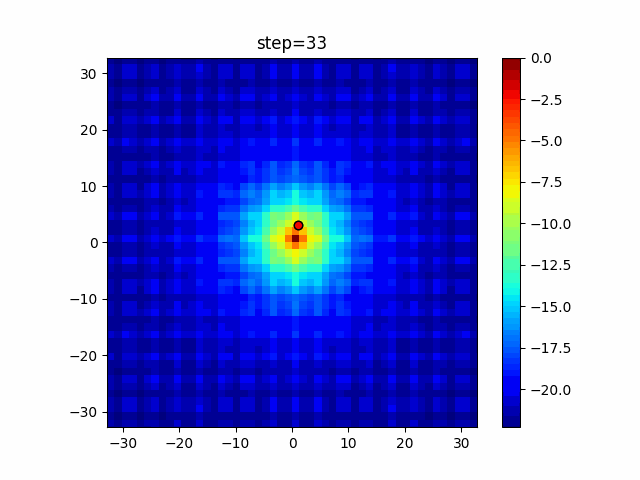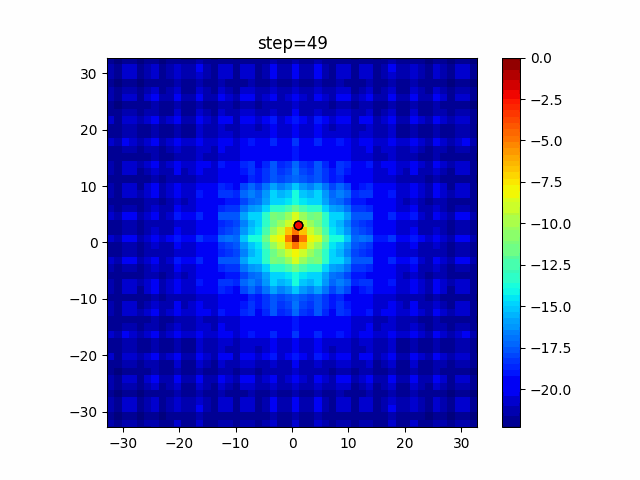
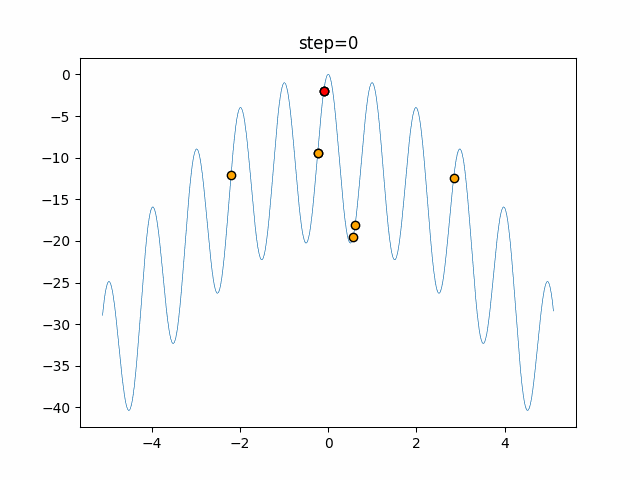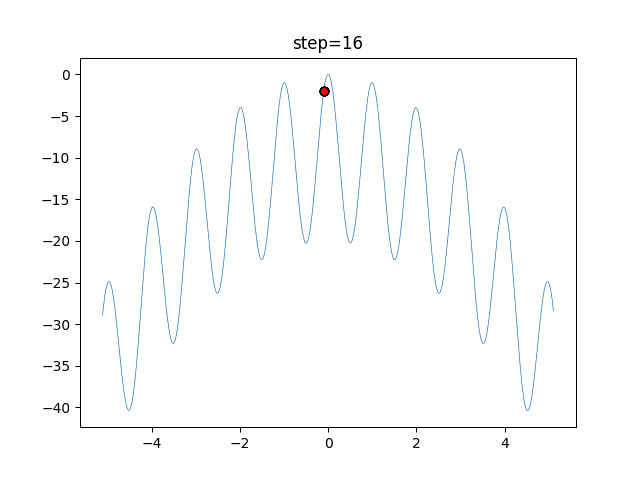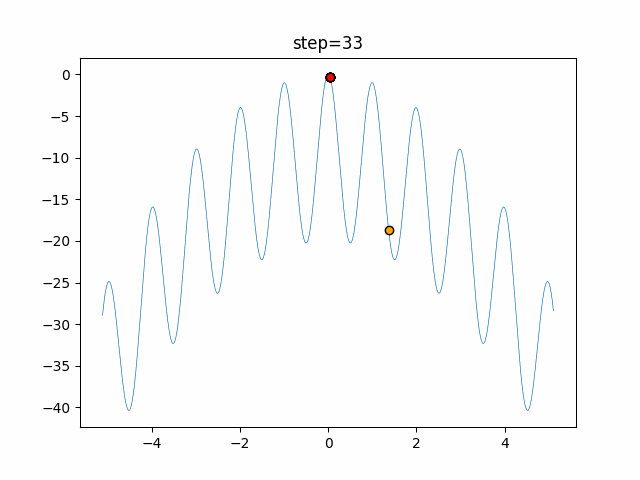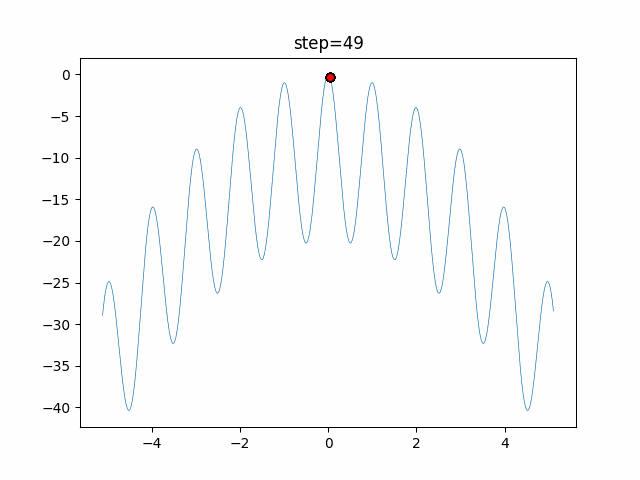
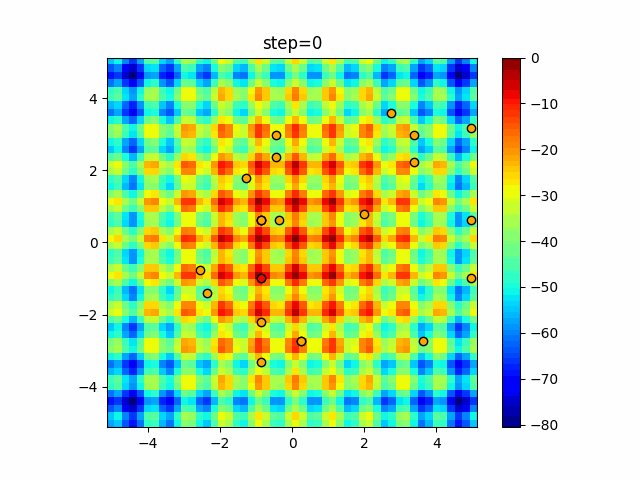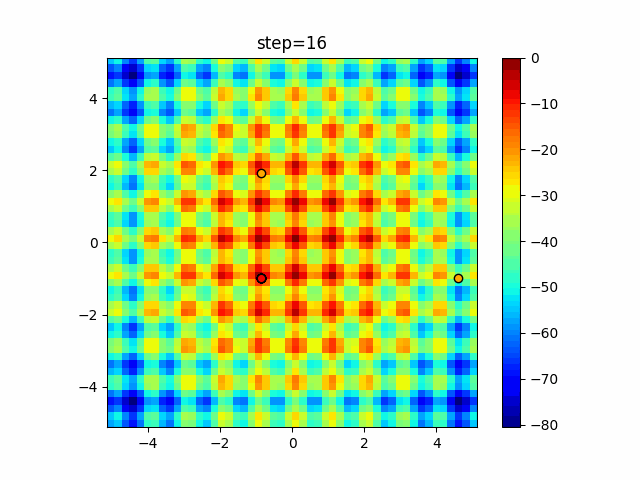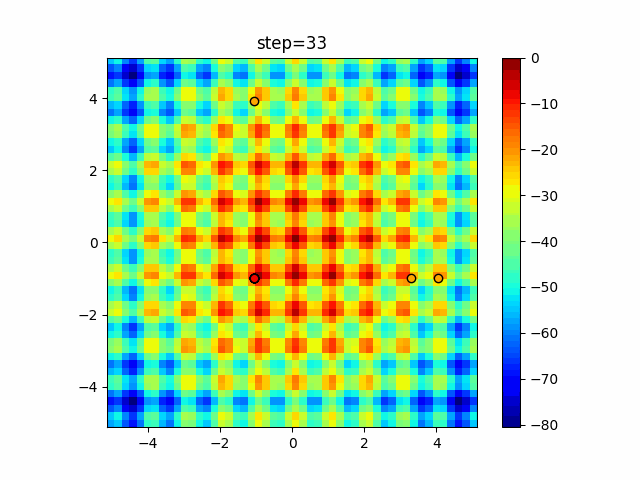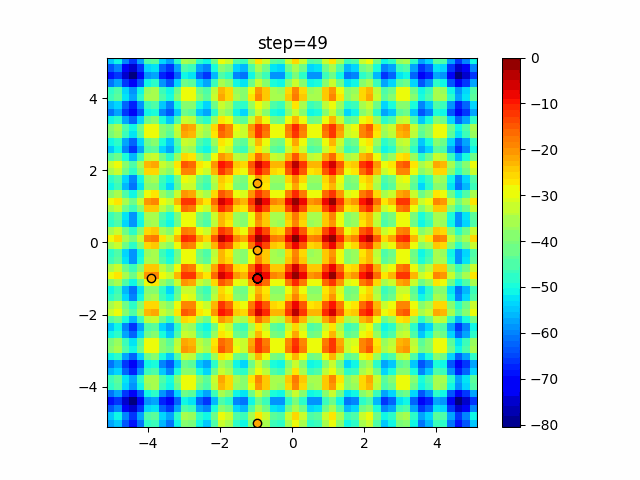
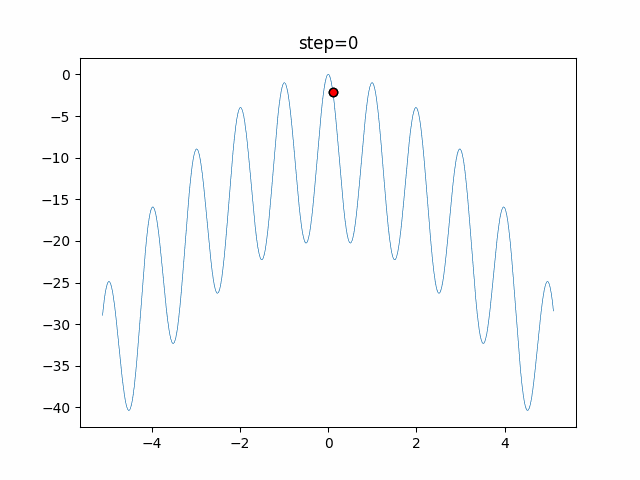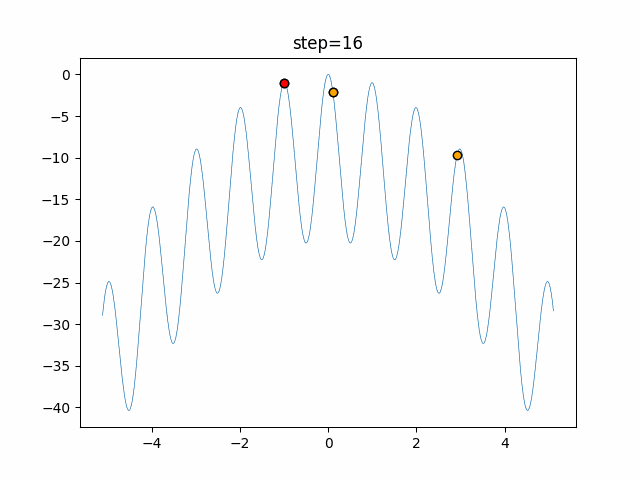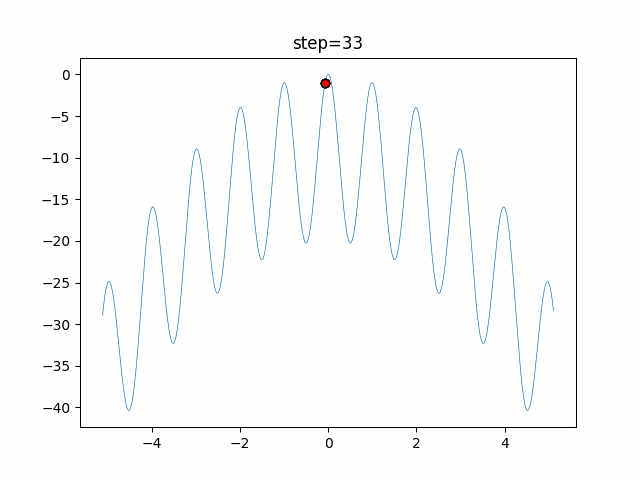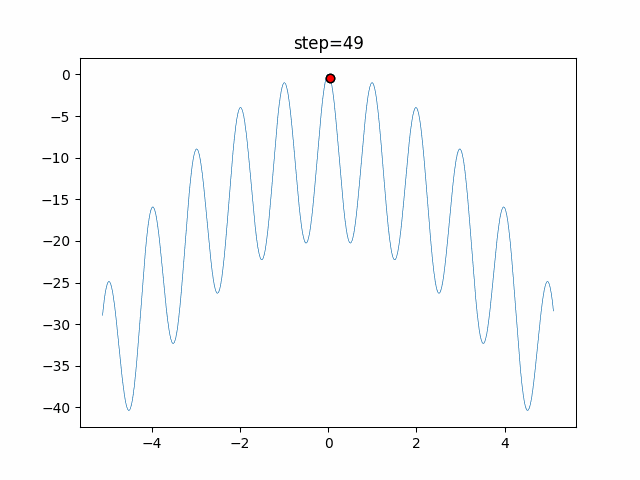
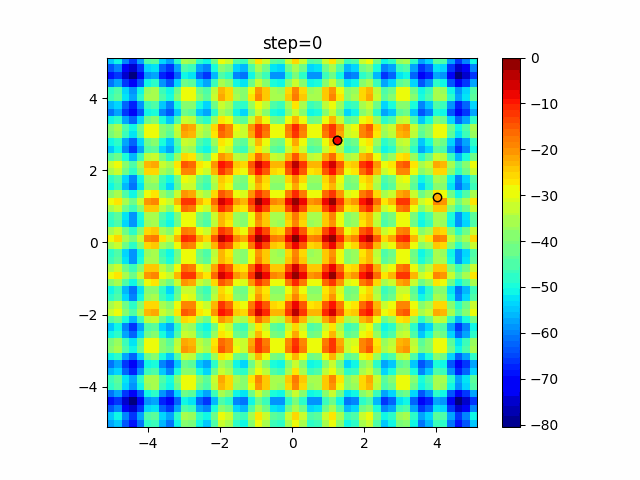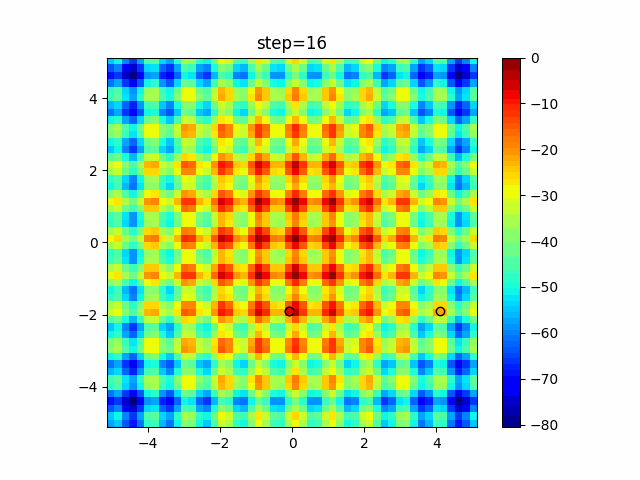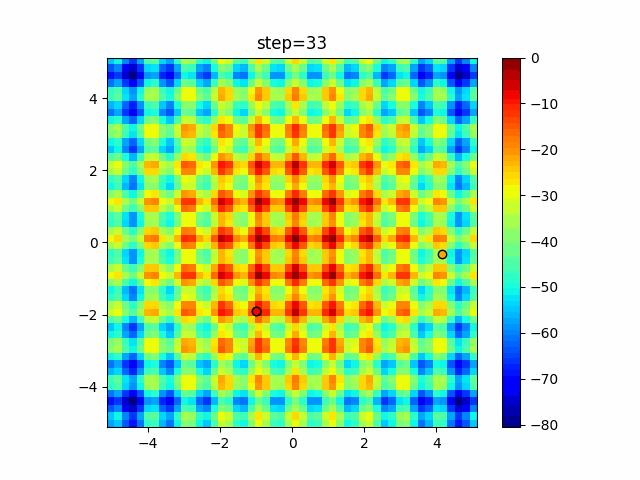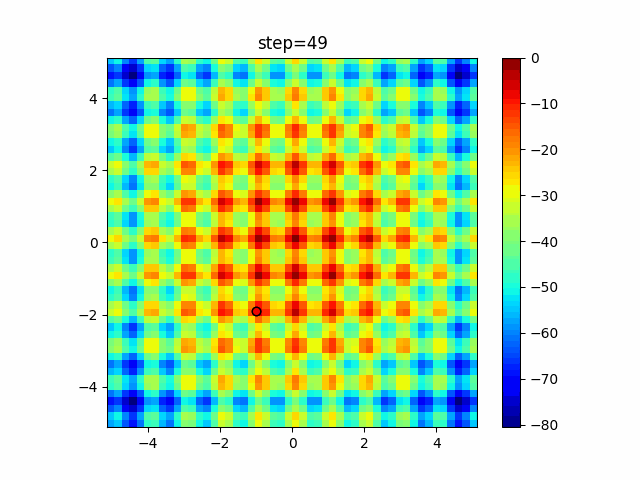
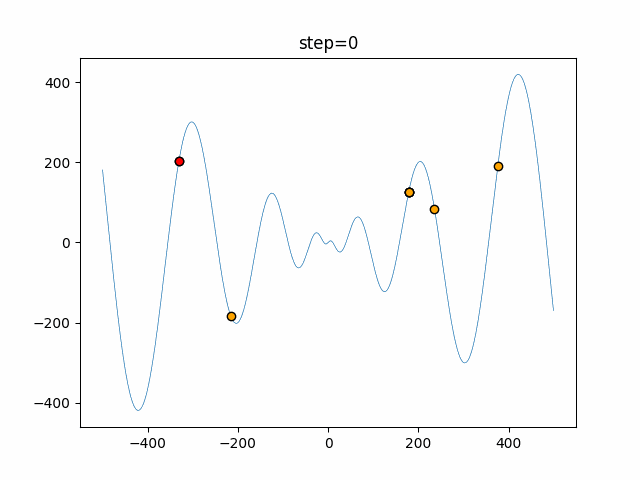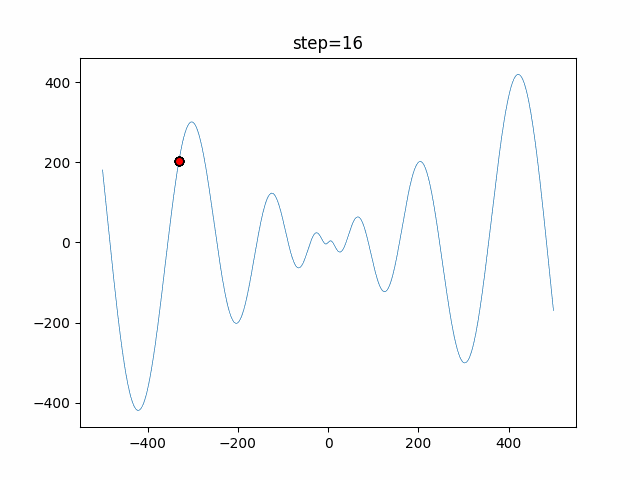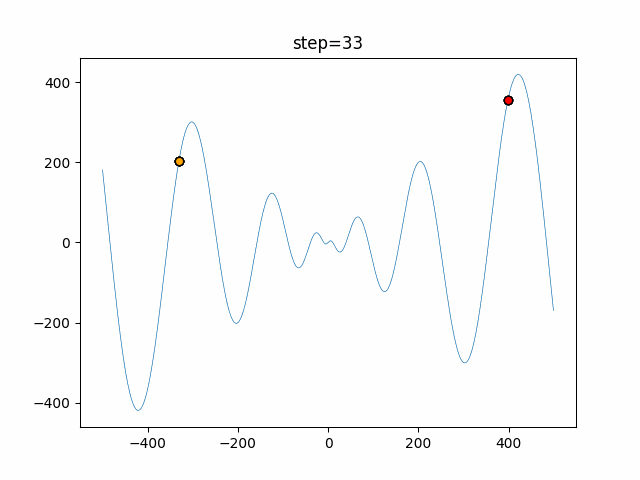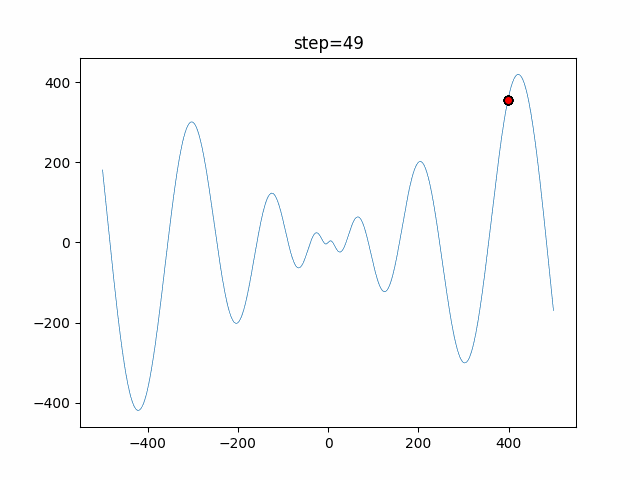
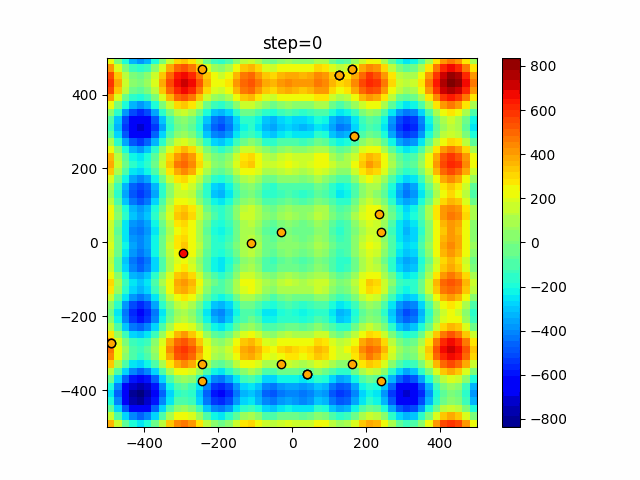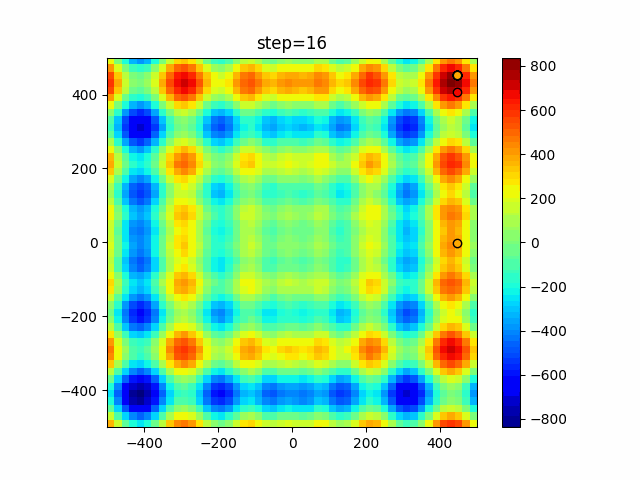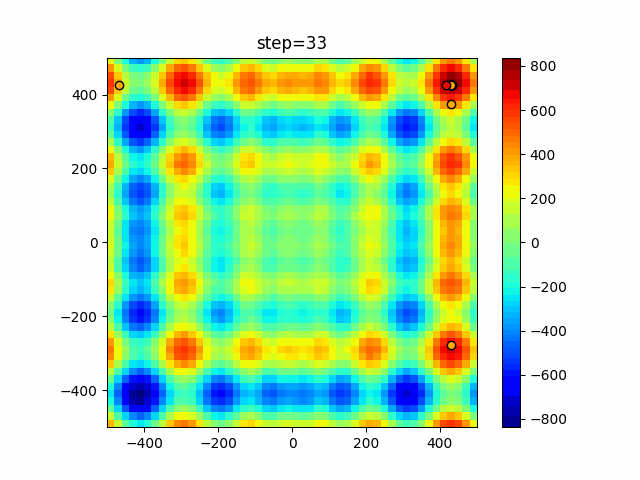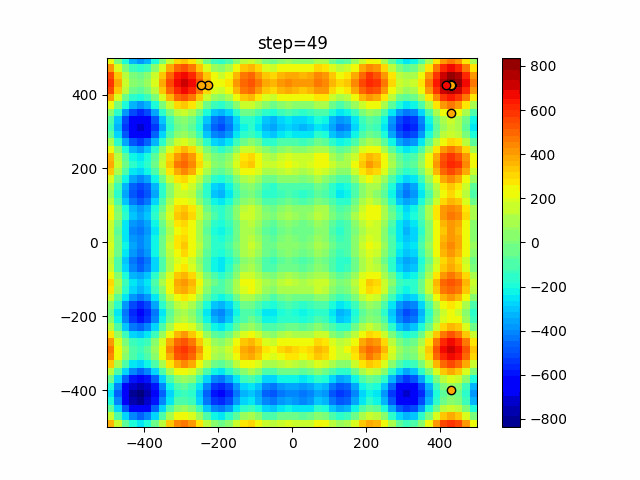
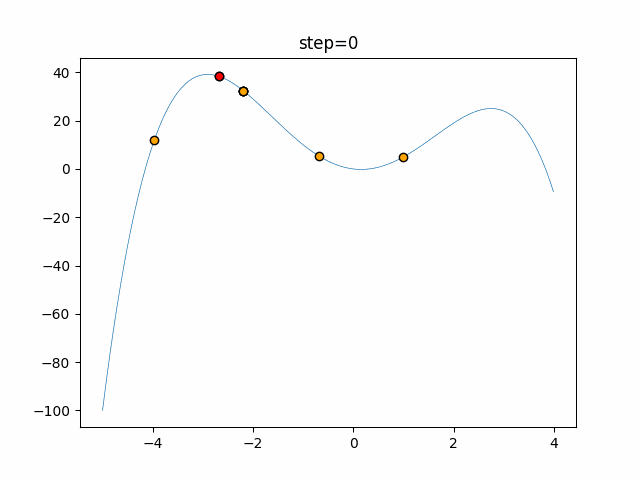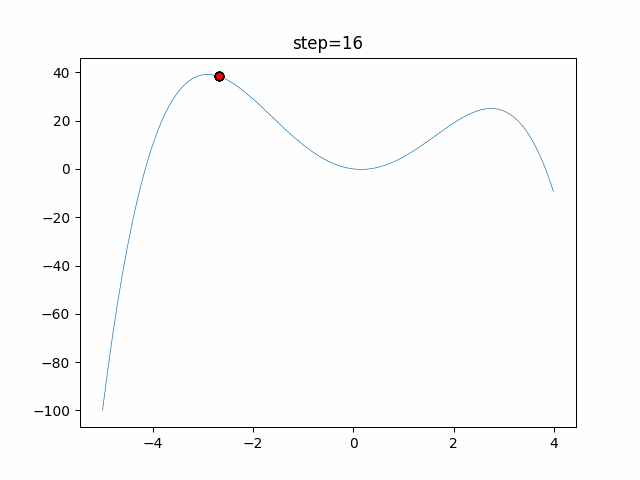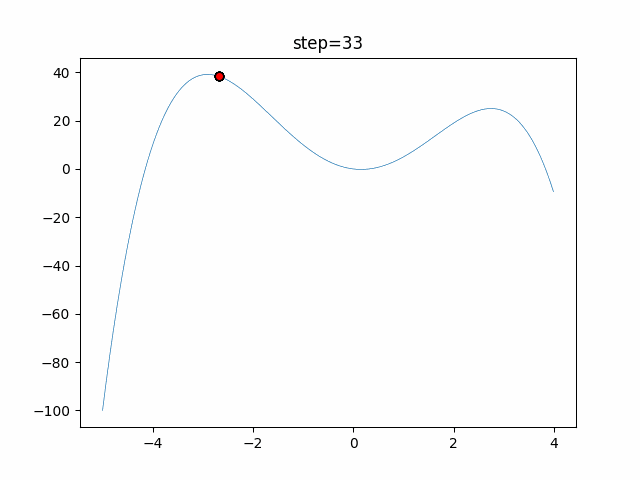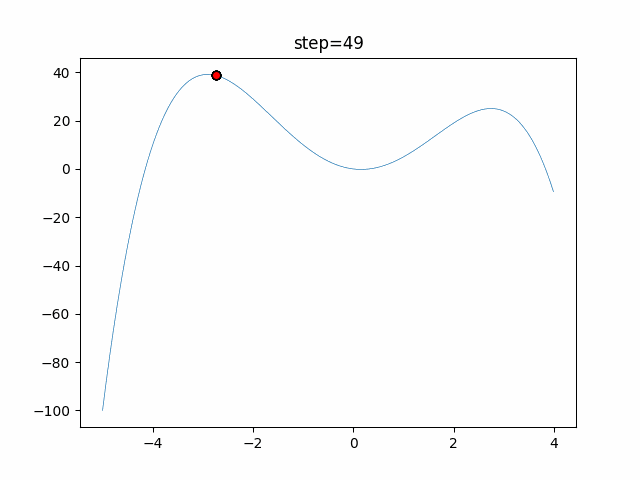
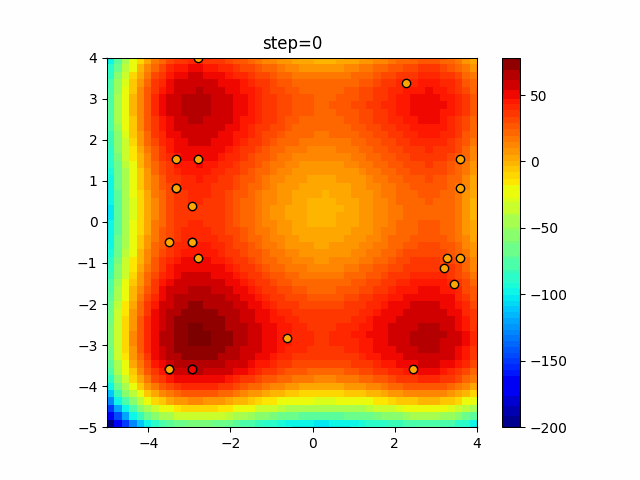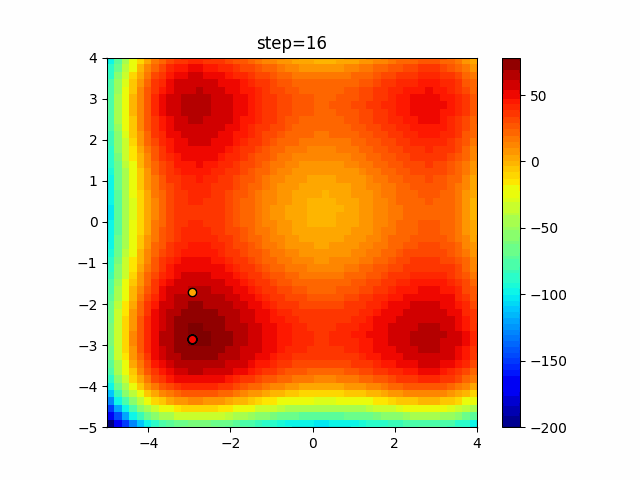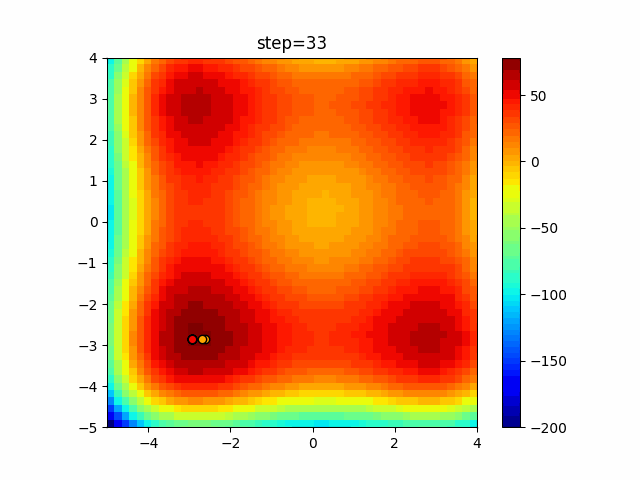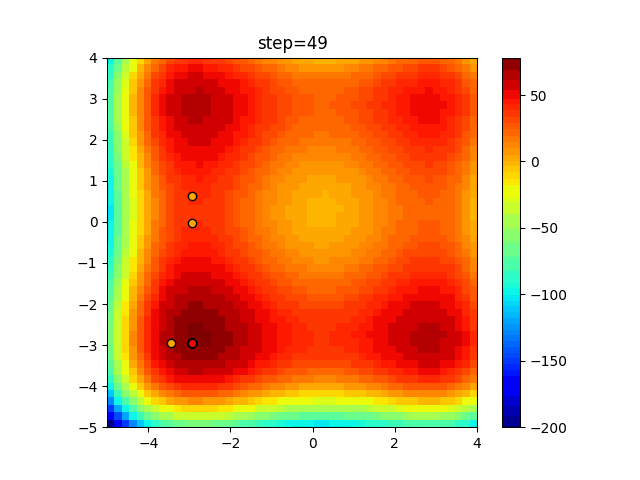
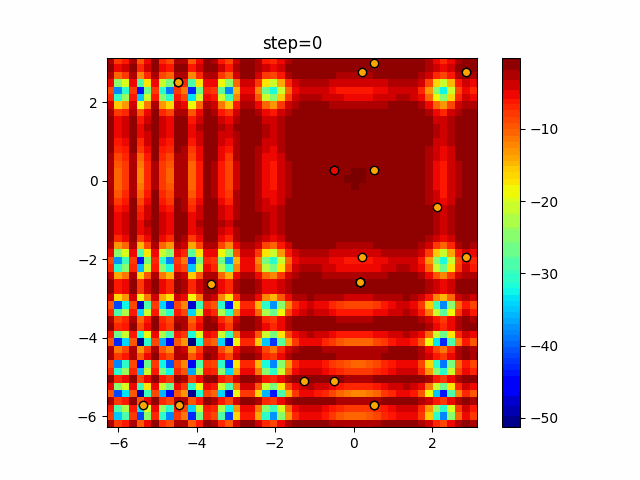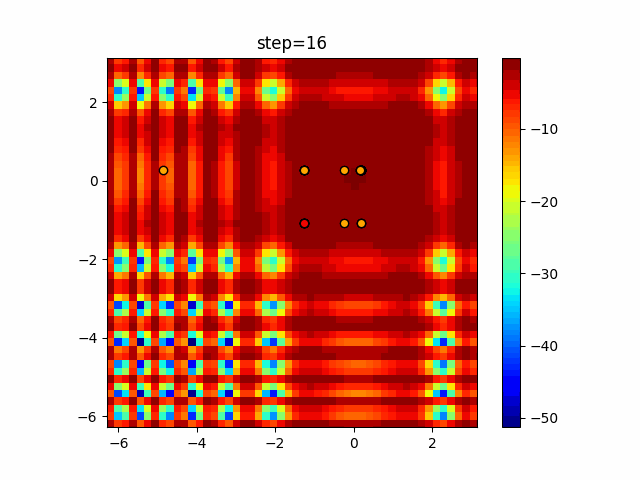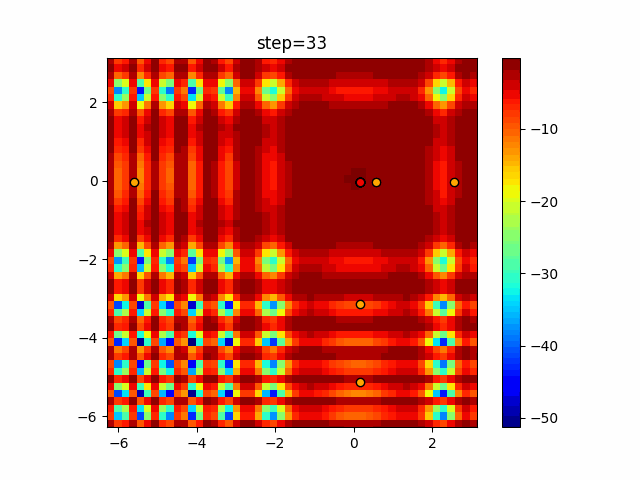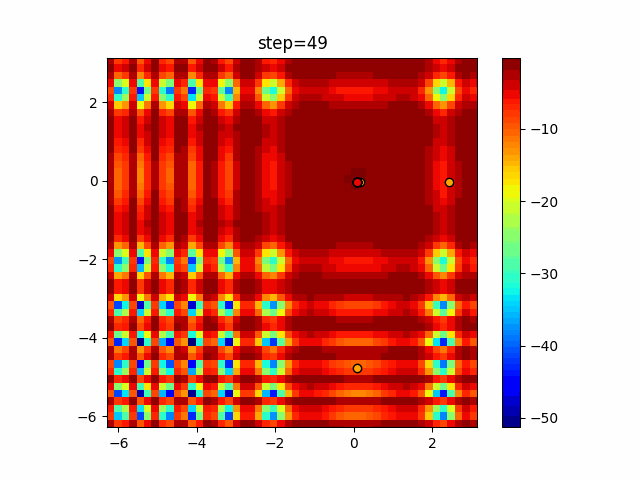
The 1st dimension is 6 individuals, and the 2nd dimension is 20 individuals, which is the result of 50 steps. Parameter-free GA remains as it is because the number of individuals cannot be specified. The red circle is the individual with the highest score in that step.
The parameters were executed below.
GA(N, save_elite=False, select_method="ranking", mutation=0.05)
PfGA(mutation=0.5)
function_Ackley
- GA
- 1D
- 2D
- PfGA
- 1D
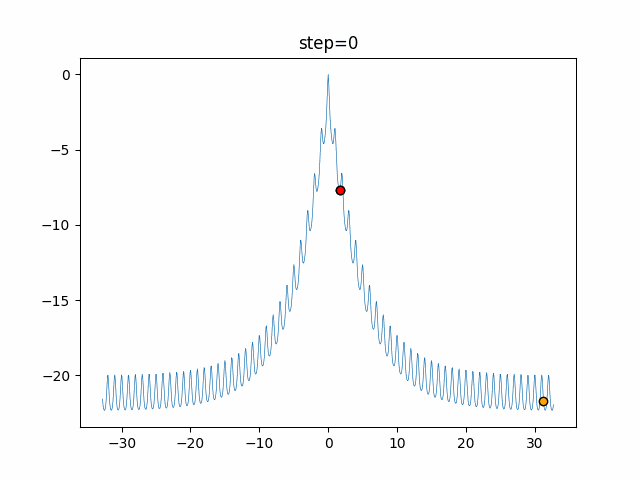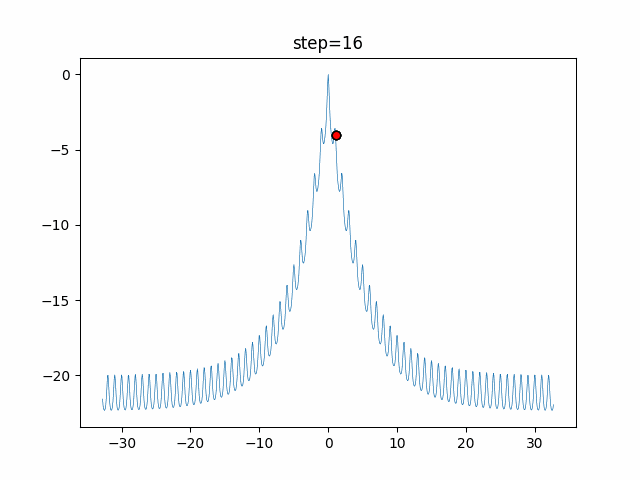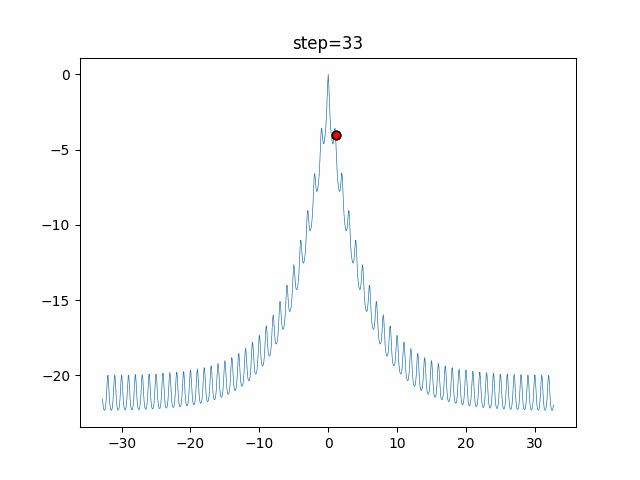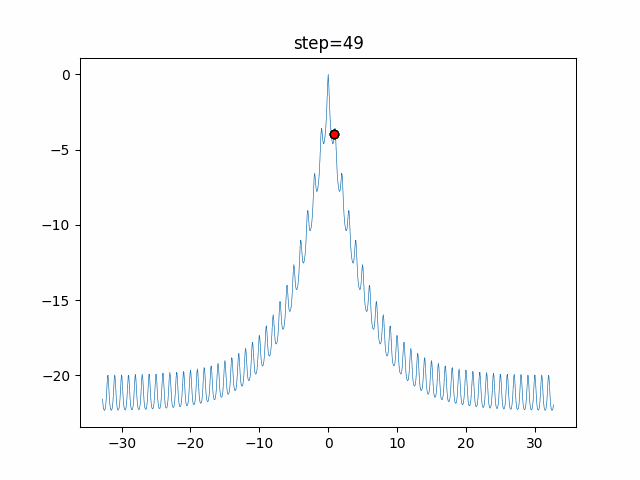
- 2D
function_Rastrigin
- GA
- 1D
- 2D
- PfGA
- 1D
- 2D
function_Schwefel
- GA
- 1D
- 2D
- PfGA
- 1D
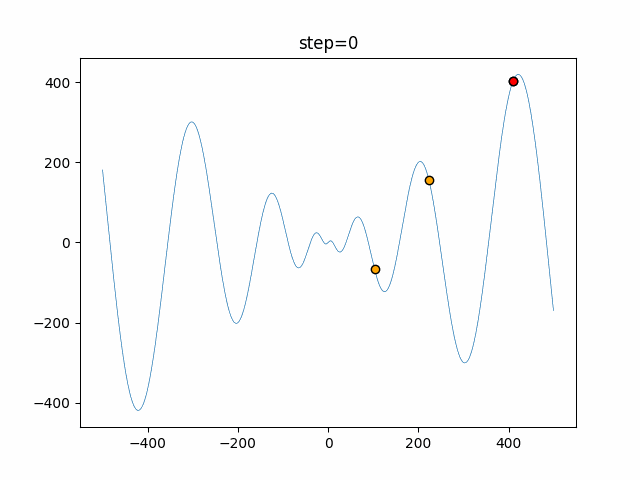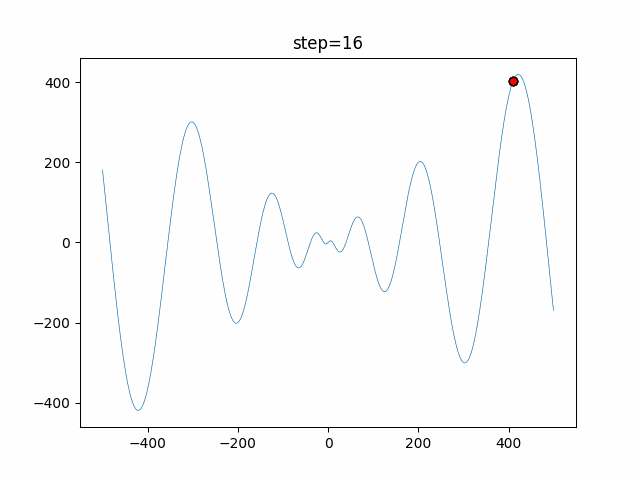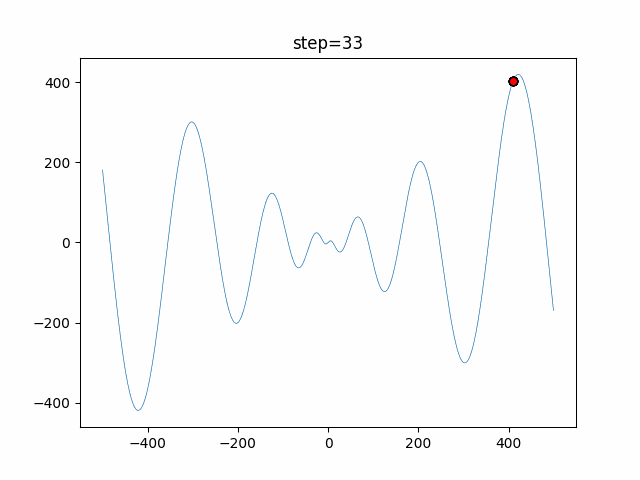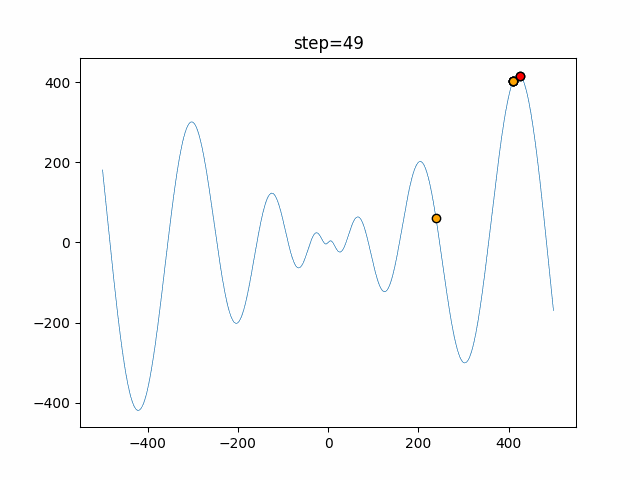
- 2D
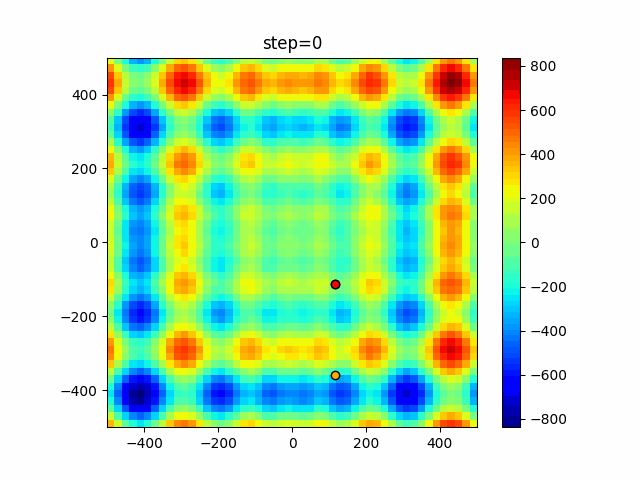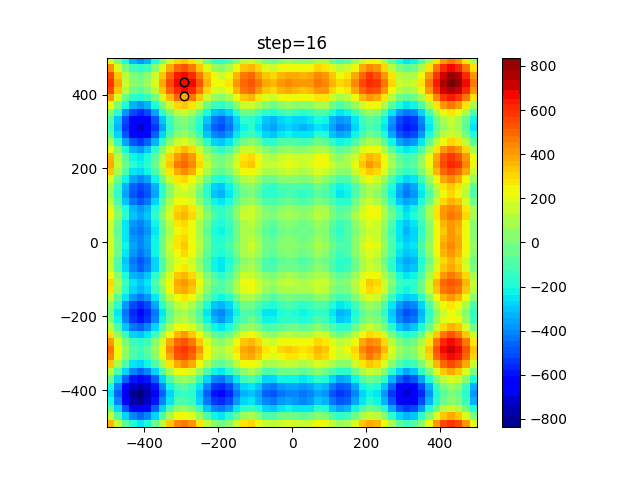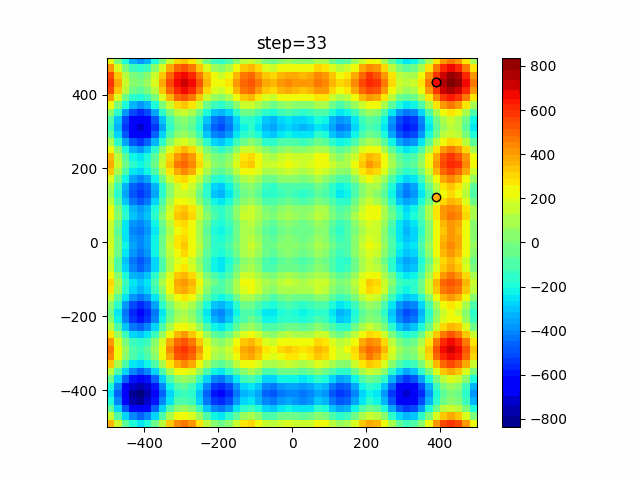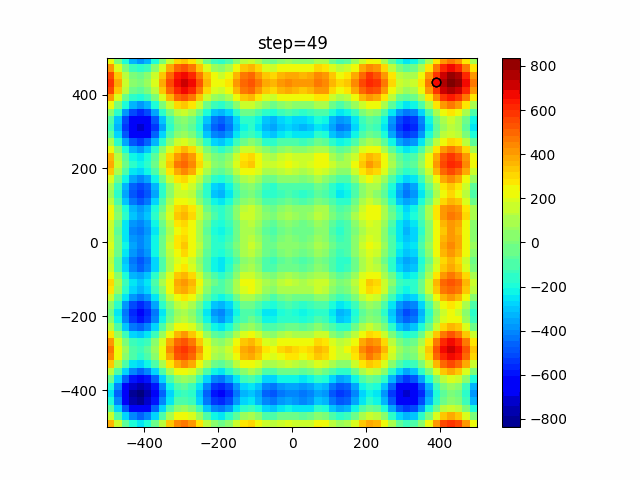
function_StyblinskiTang
- GA
- 1D
- 2D
- PfGA
- 1D
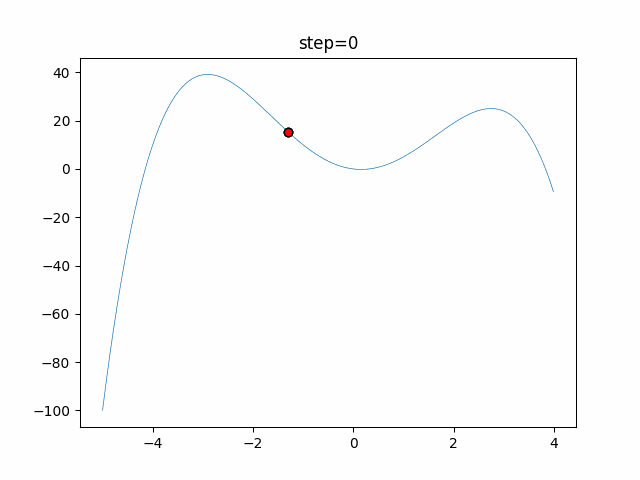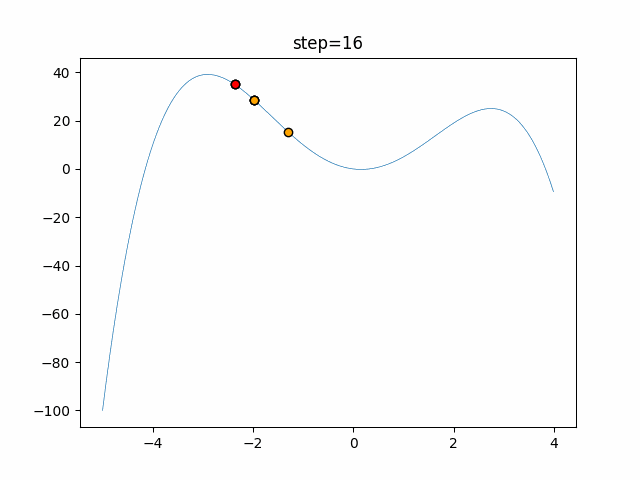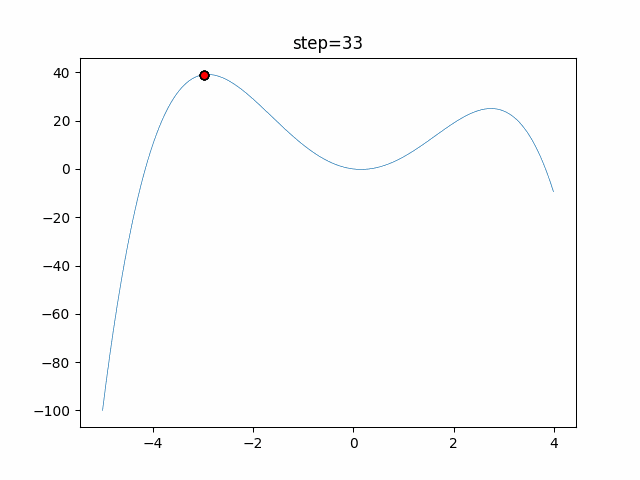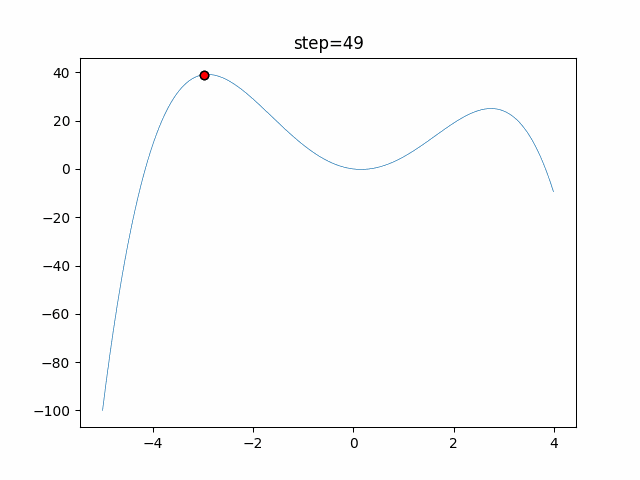
- 2D
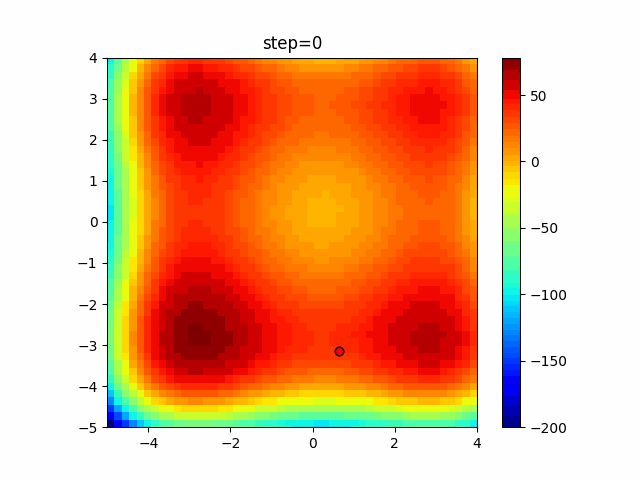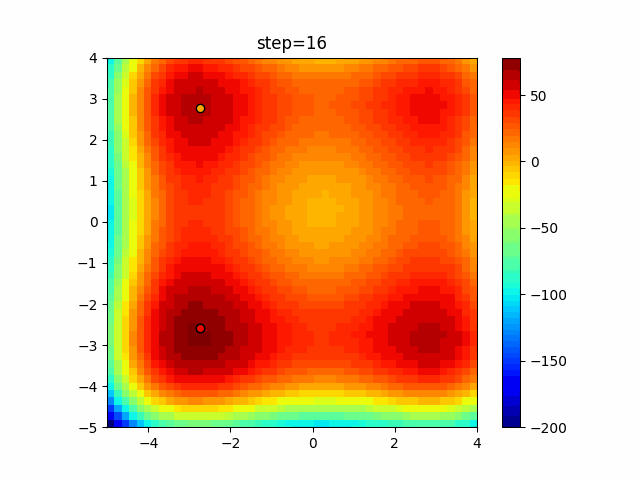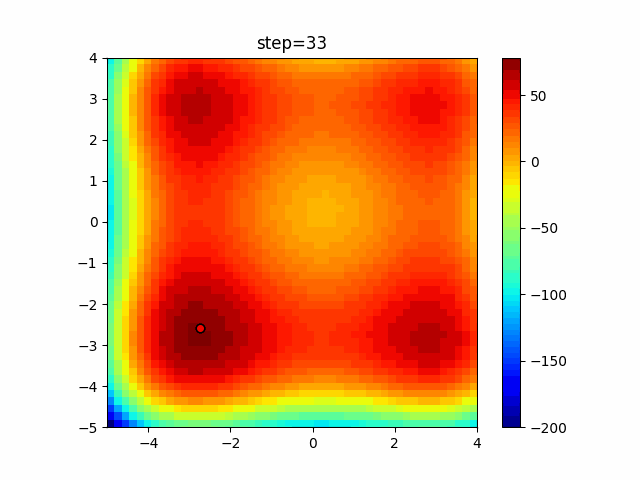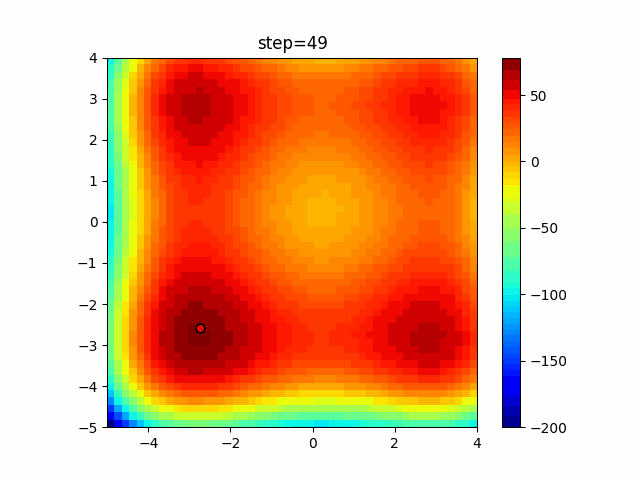
function_XinSheYang
- GA
- 1D

- 2D
- PfGA
- 1D

- 2D

Afterword
Since the intersection is a dimensional unit, the one-dimensional result is not very helpful. (Only random movement in mutation) The characteristic of uniform crossing is that there are many individuals in the vertical and horizontal positions in two dimensions. Although it is a uniform crossover, since this is a crossover that targets discrete values, it may give different results if it is a crossover that targets real values (BLX-α crossover or simplex crossover). (Maybe it will be implemented soon?)
By the way, regarding the probability of mutation, if it is set to 0%, it will converge to the highest rated individual.
Recommended Posts