We will implement the optimization algorithm (harmony search)
Introduction
A series of optimization algorithm implementations. First, look at Overview.
The code can be found on github.
Harmony search
Overview
Harmony Search is an algorithm created by focusing on the thoughts of musicians when improvising. I think the musician has decided the original phrase of the following idea.
- Play frequently used phrases as they are
- Adjust and play frequently used phrases
- Create and play a new phrase
algorithm
- Algorithm flow


- Term correspondence
| problem | Harmony search |
|---|---|
| One element of input | Chord (phrase) |
| Input to the problem | harmony |
| Evaluation value | ハーモニーのEvaluation value |
- Regarding hyperparameters
| Variable name | meaning | Remarks |
|---|---|---|
| bandwidth | Bandwidth | Adjustment rate when adjusting chords |
| select_rate | Probability of generating a new chord | |
| change_rate | Probability of adjusting chords |
Duplicate chords
Use the target chord as it is.
x^{new}_i = x^r_i
Adjust and use chords
Adjust with the following formula.
$ B $ is the bandwidth, a user-specified variable.
Bandwidth improvement
This article is original.
In the above formula, the value of $ B $ is highly dependent on the lower and upper limits of the one element in question. So instead of using $ B $ directly, I chose a percentage.
Whole code
import math
import random
class Harmony():
def __init__(self,
harmony_max,
bandwidth=0.1,
enable_bandwidth_rate=False, #Whether bandwidth is a percentage or a value
select_rate=0.8,
change_rate=0.3,
):
self.harmony_max = harmony_max
self.bandwidth = bandwidth
self.enable_bandwidth_rate = enable_bandwidth_rate
self.select_rate = select_rate
self.change_rate = change_rate
def init(self, problem):
self.problem = problem
self.harmonys = []
for _ in range(self.harmony_max):
self.harmonys.append(problem.create())
def step(self):
#Create a new harmony
arr = []
for i in range(self.problem.size):
if random.random() < self.select_rate:
#Generate new chords
arr.append(self.problem.randomVal())
continue
#Select one harmony
h_arr = self.harmonys[random.randint(0, self.harmony_max-1)].getArray()
if random.random() < self.change_rate:
#Change chords
if self.enable_bandwidth_rate:
#Specify bandwidth as a percentage
bandwidth = self.bandwidth * (self.problem.MAX_VAL - self.problem.MIN_VAL)
else:
bandwidth = self.bandwidth
n = h_arr[i] + bandwidth * (random.random()*2-1)
arr.append(n)
else:
#Duplicate chords
arr.append(h_arr[i])
harmony = self.problem.create(arr)
#Replace if the new harmony has a higher rating than the worst harmony
self.harmonys.sort(key=lambda x: x.getScore())
if self.harmonys[0].getScore() < harmony.getScore():
self.harmonys[0] = harmony
Hyperparameter example
It is the result of optimizing hyperparameters with optuna for each problem. One optimization trial yields results with a search time of 5 seconds. I did this 100 times and asked optuna to find the best hyperparameters.
| problem | bandwidth | change_rate | enable_bandwidth_rate | harmony_max | select_rate |
|---|---|---|---|---|---|
| EightQueen | 0.199731235367978 | 0.007945406417271816 | False | 8 | 0.05285166540946163 |
| function_Ackley | 0.6478593586012942 | 0.37819472248801433 | False | 24 | 0.0045960067336094125 |
| function_Griewank | 0.957845478793464 | 0.6531645473958932 | False | 19 | 0.0065542485084037 |
| function_Michalewicz | 0.3020087834816175 | 0.0063312721531867296 | False | 8 | 0.009704544614251957 |
| function_Rastrigin | 0.9244843154507476 | 0.003091269983721383 | False | 19 | 0.005363972453695971 |
| function_Schwefel | 0.6525179901987925 | 0.6847228820427808 | False | 24 | 0.017390991518258108 |
| function_StyblinskiTang | 0.012259017079907453 | 0.005592287367206683 | True | 5 | 0.010574637751612243 |
| function_XinSheYang | 0.021452540527582796 | 0.5116052912533812 | False | 43 | 0.000560227904147548 |
| g2048 | 0.5208515497767559 | 0.9192443470308422 | False | 6 | 0.025020522147974456 |
| LifeGame | 0.12412374231584394 | 0.3047344866221531 | True | 15 | 0.3351269586087304 |
| OneMax | 0.6404754184189828 | 0.11674742823674397 | True | 3 | 0.21323358379499358 |
| TSP | 0.9991577906059103 | 0.026545669987045384 | False | 35 | 0.026355483052867487 |
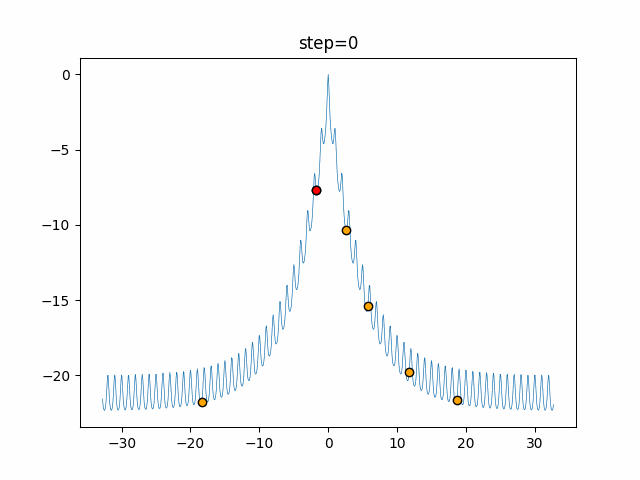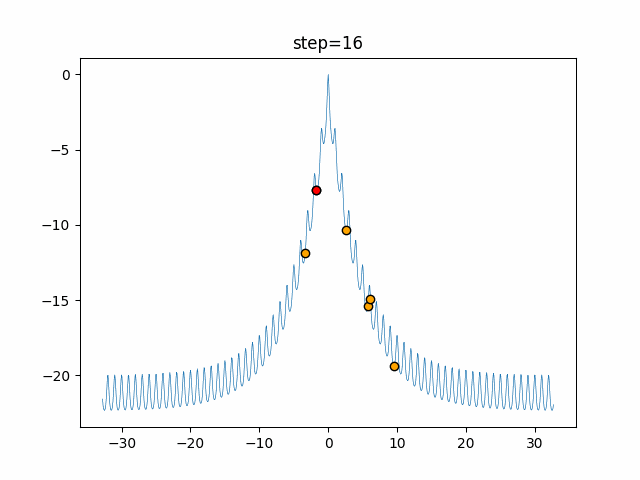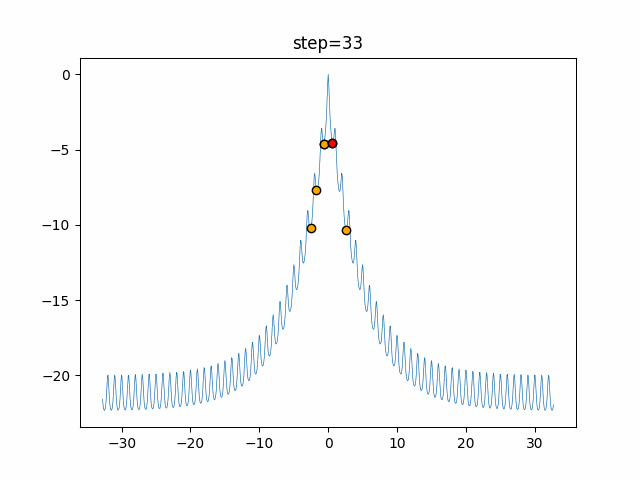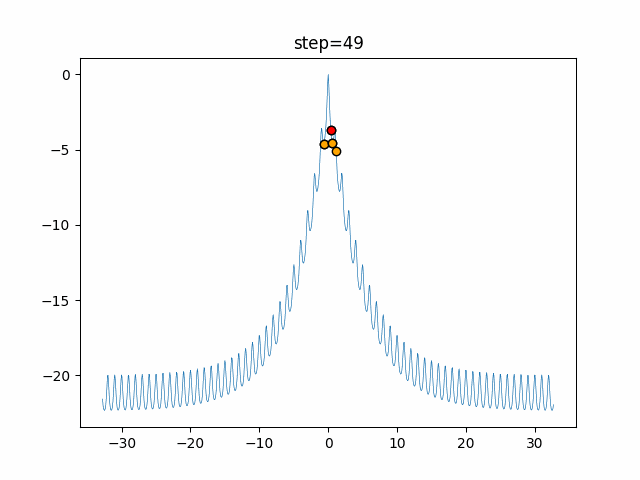
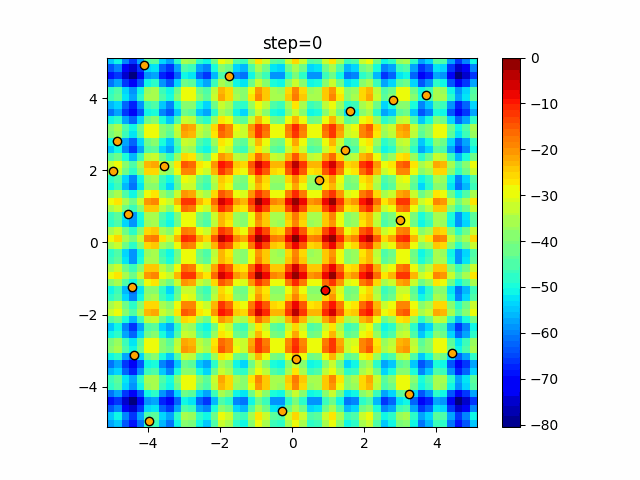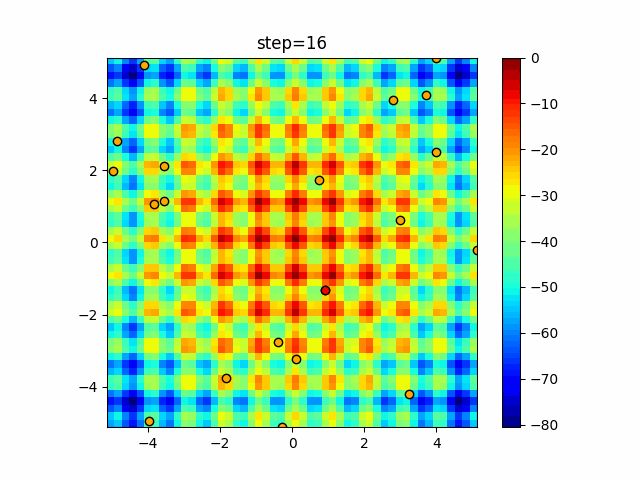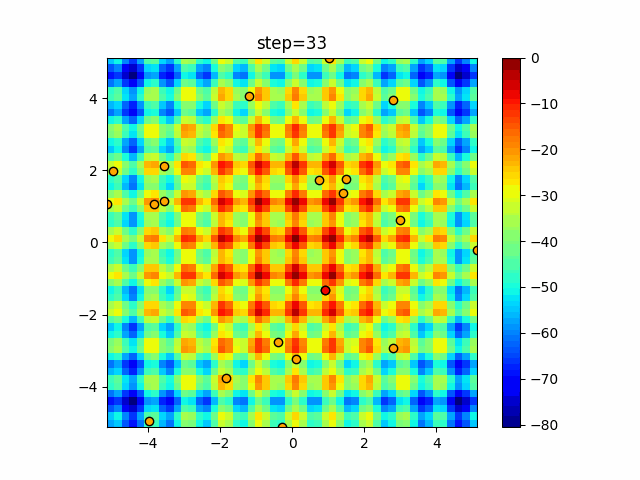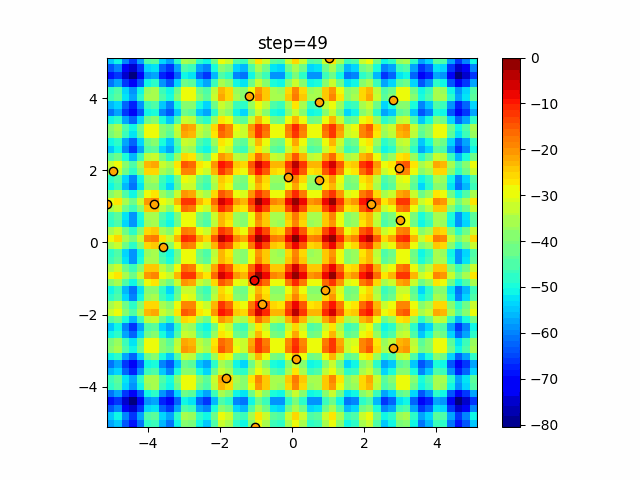
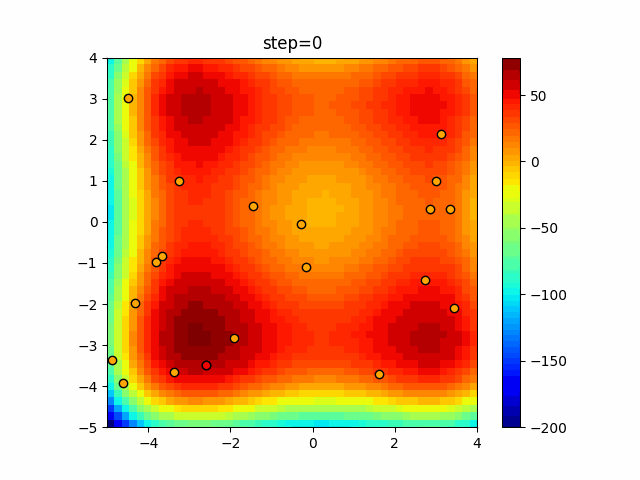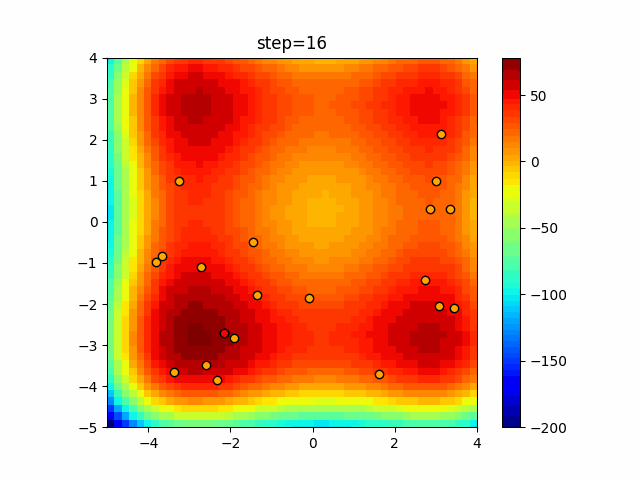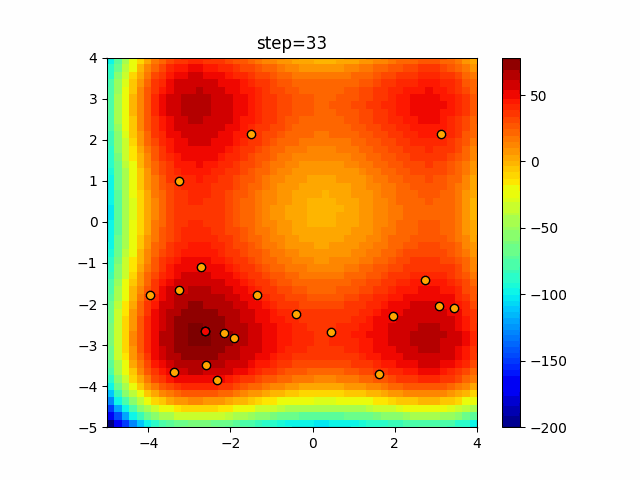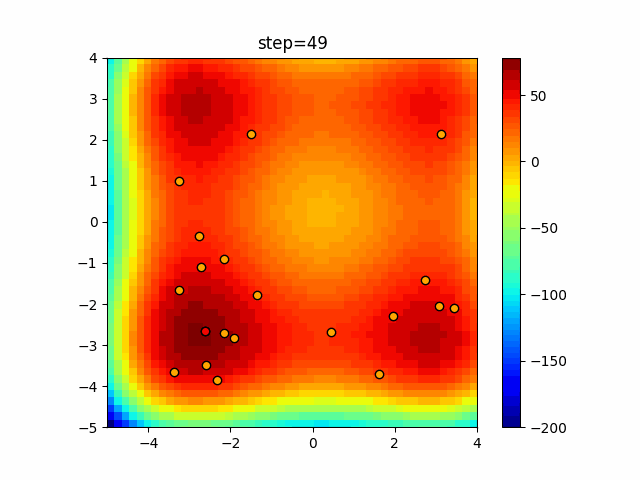
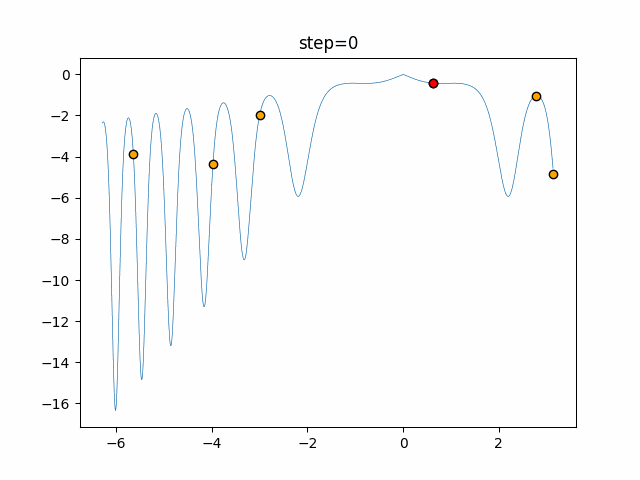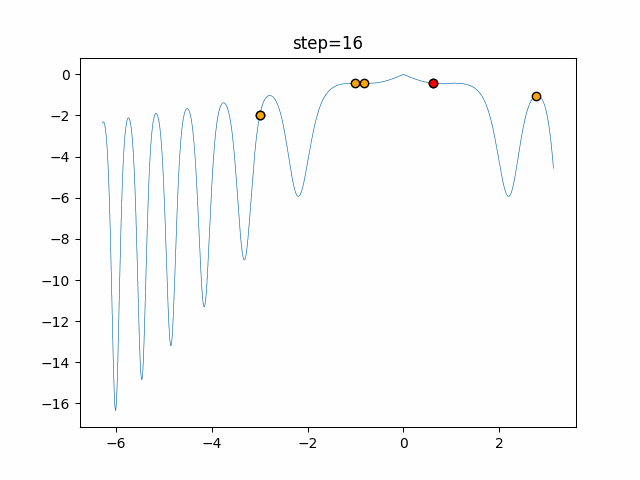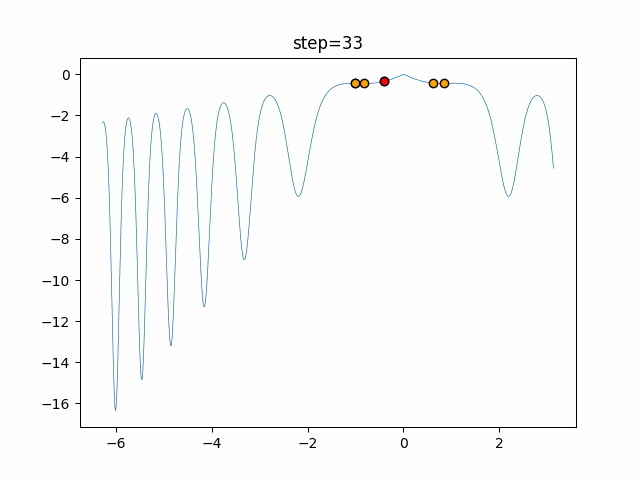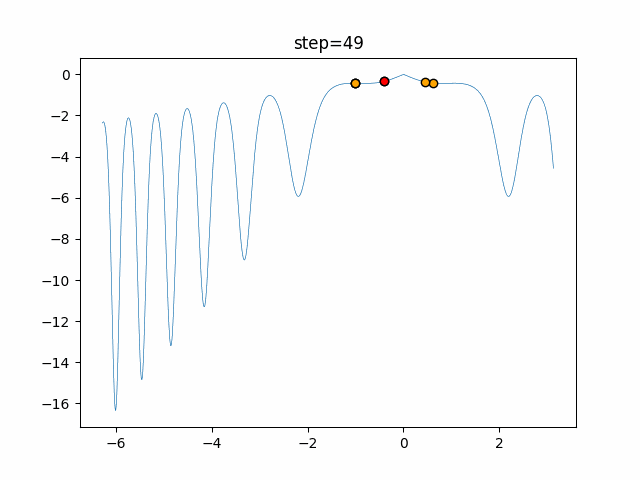
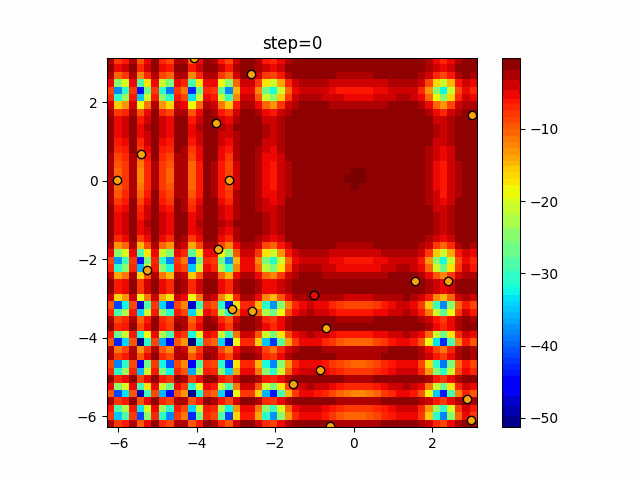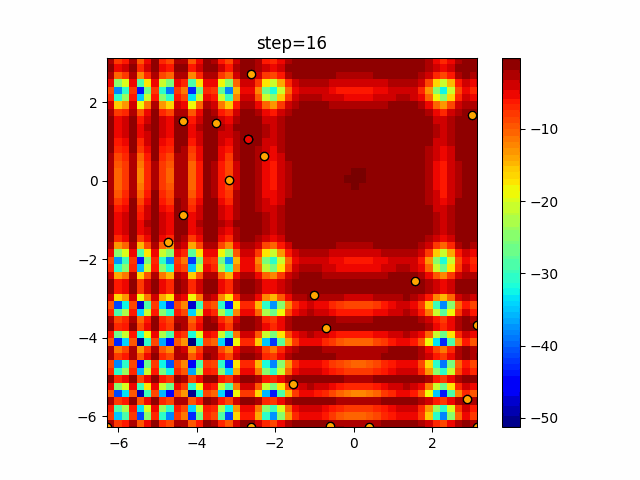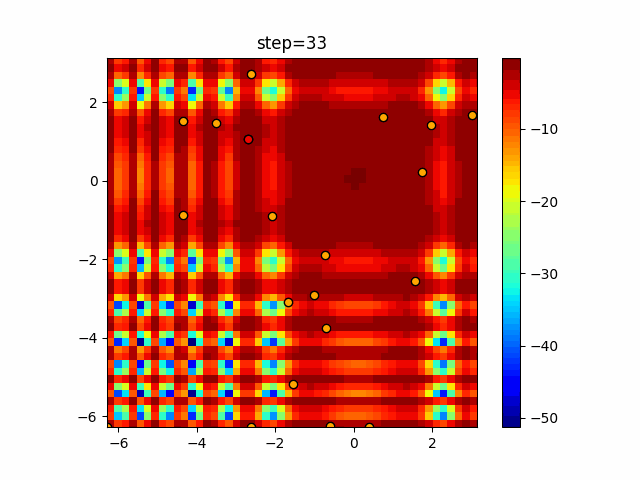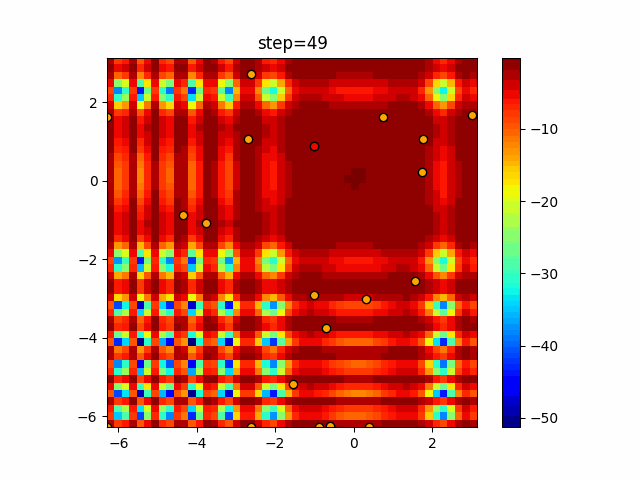
Visualization of actual movement
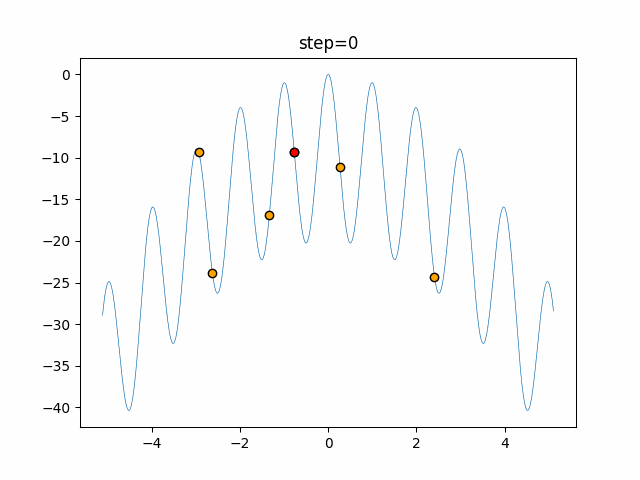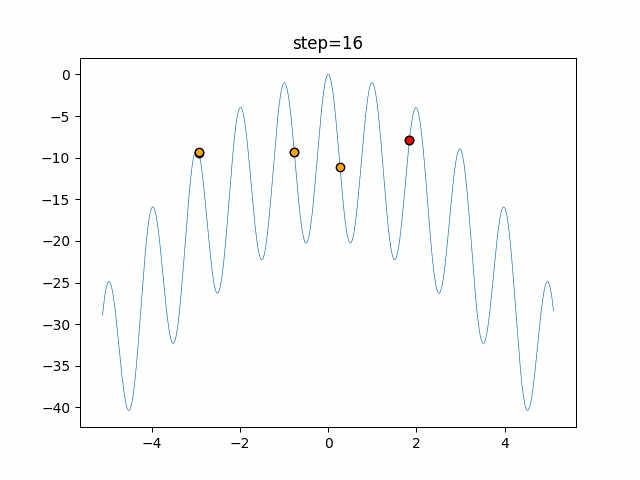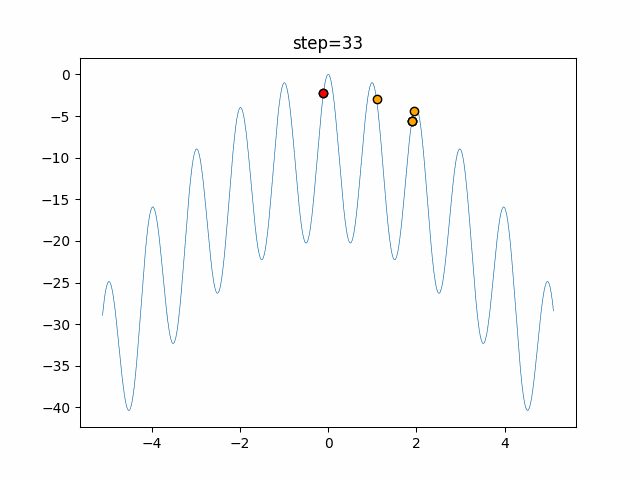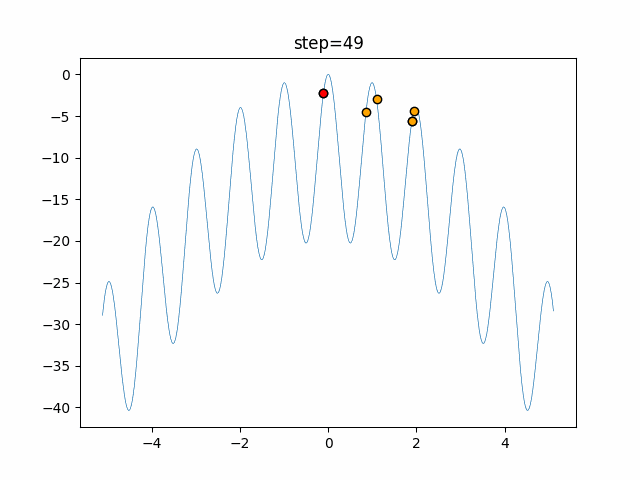
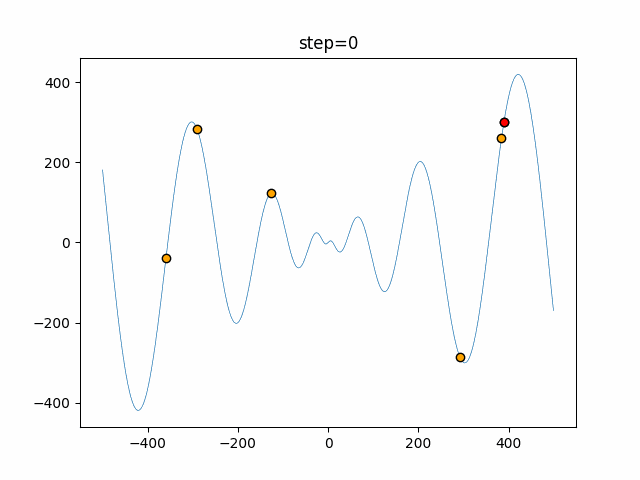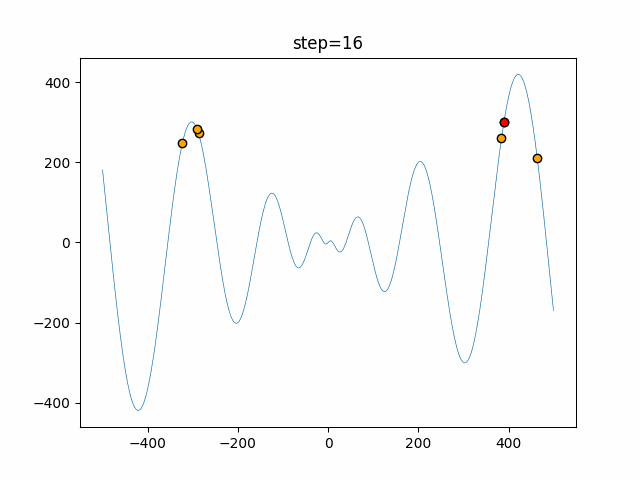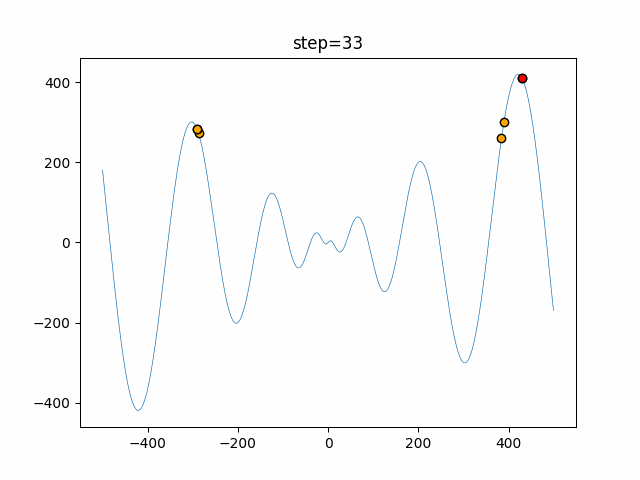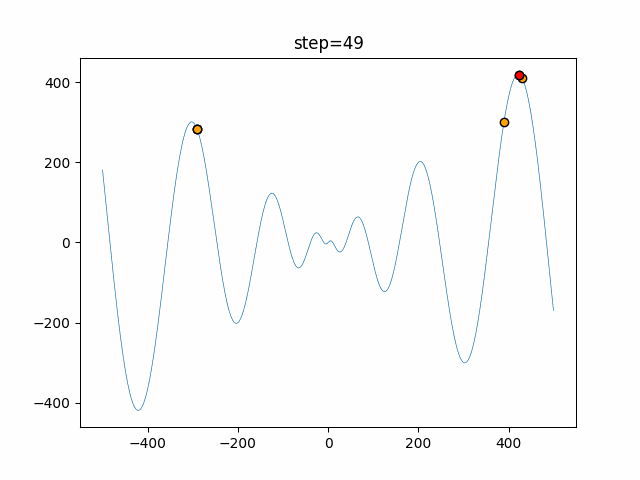
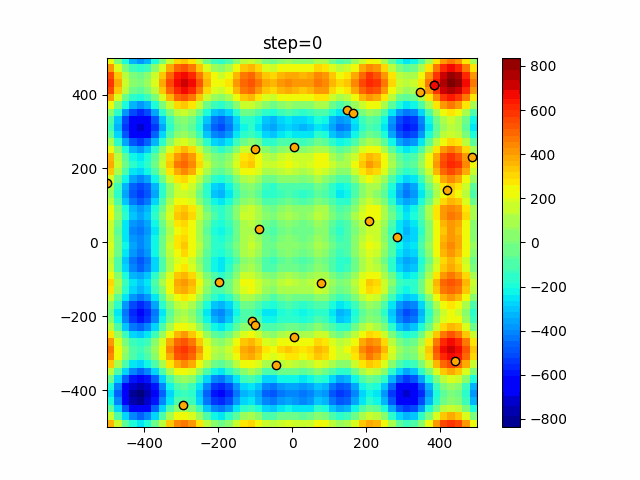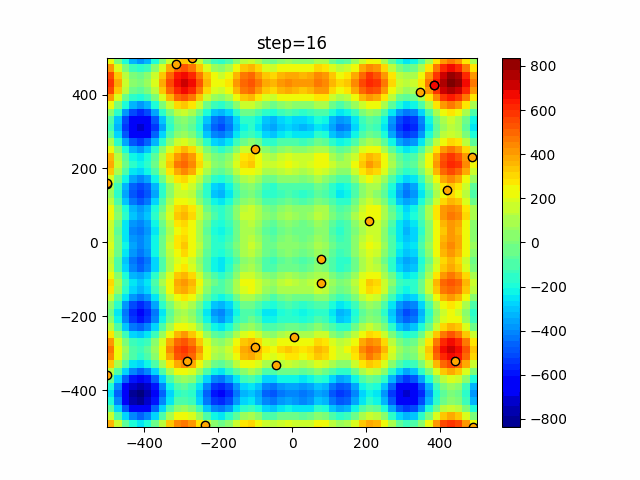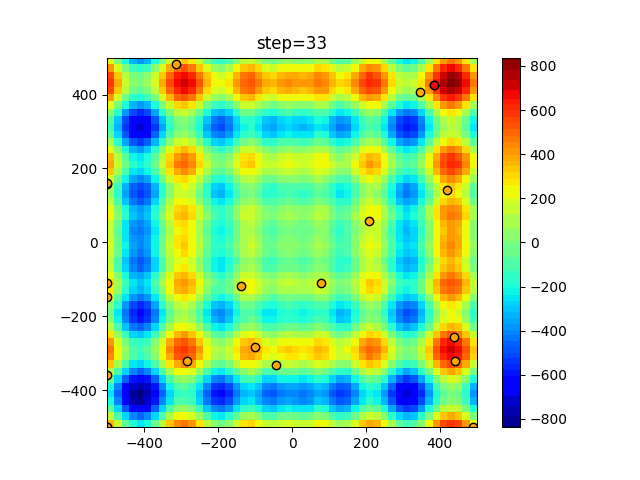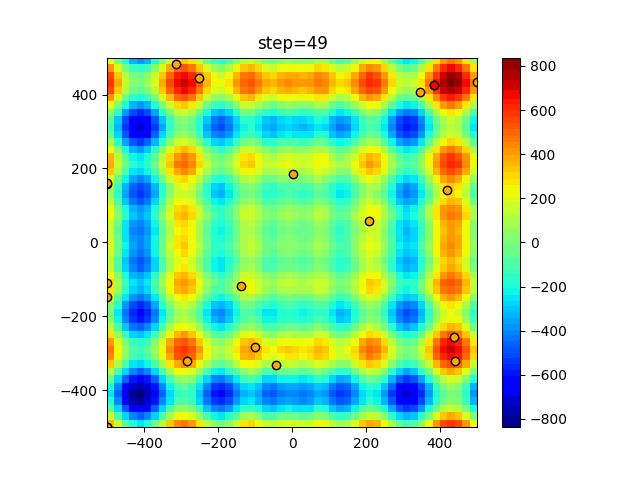
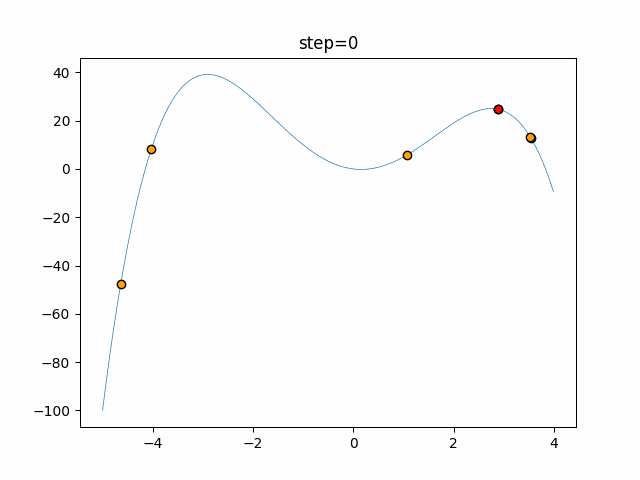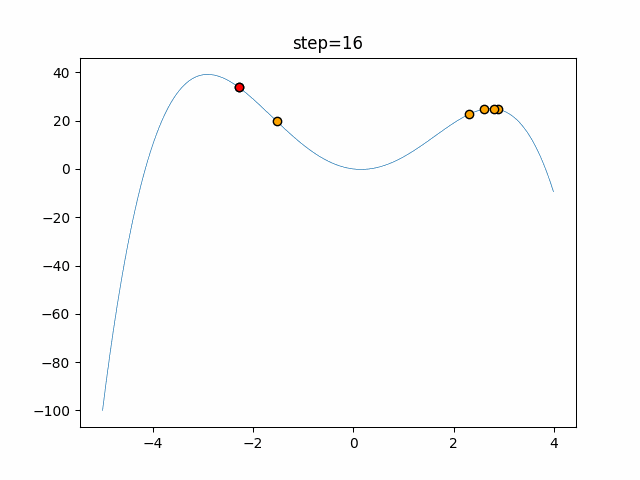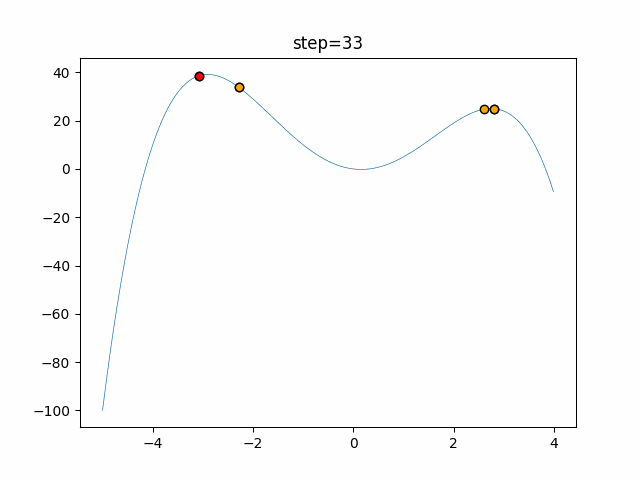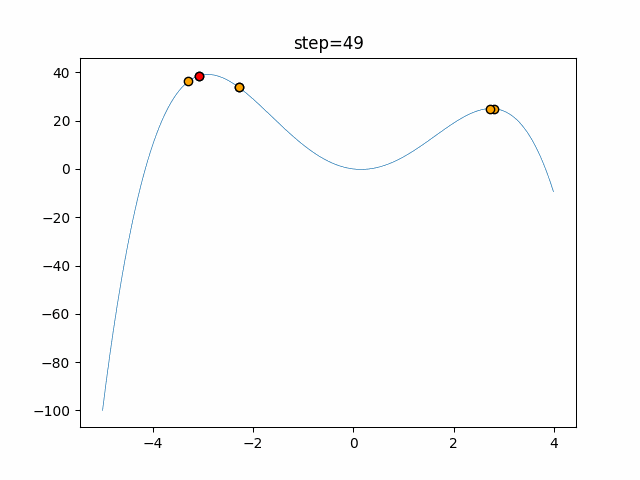
The 1st dimension is 6 individuals, and the 2nd dimension is 20 individuals, which is the result of 50 steps. The red circle is the individual with the highest score in that step.
The parameters were executed below.
Harmony(N, bandwidth=1.0, enable_bandwidth_rate=True, select_rate=0.4, change_rate=0.9)
function_Ackley
- 1D
- 2D
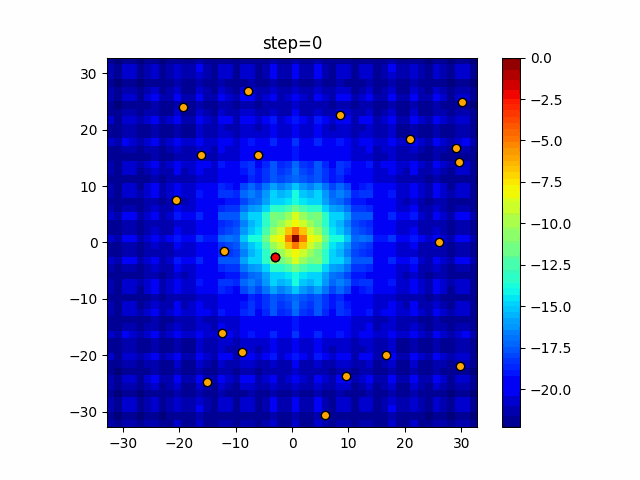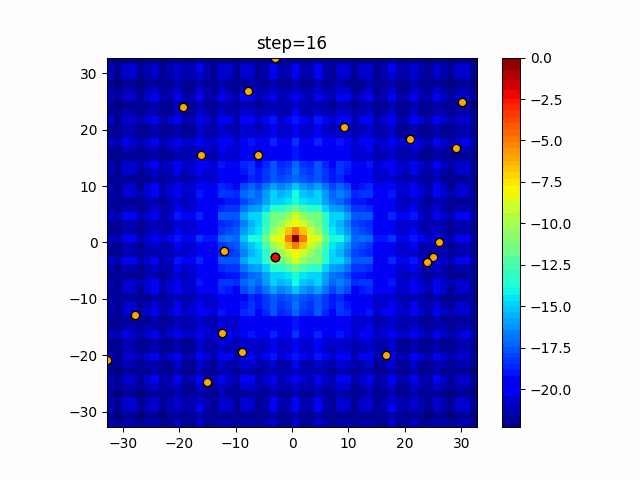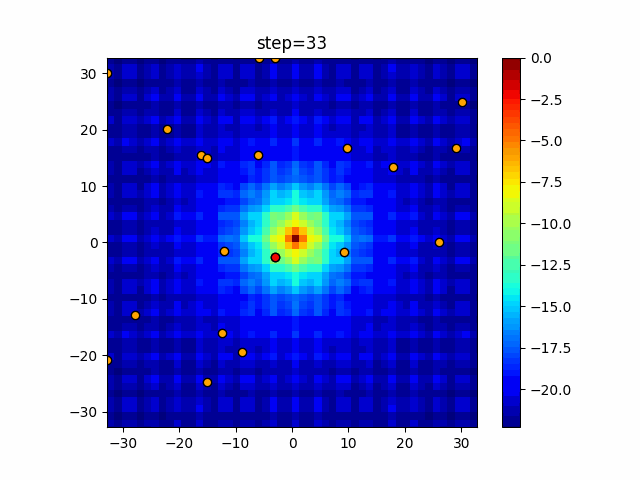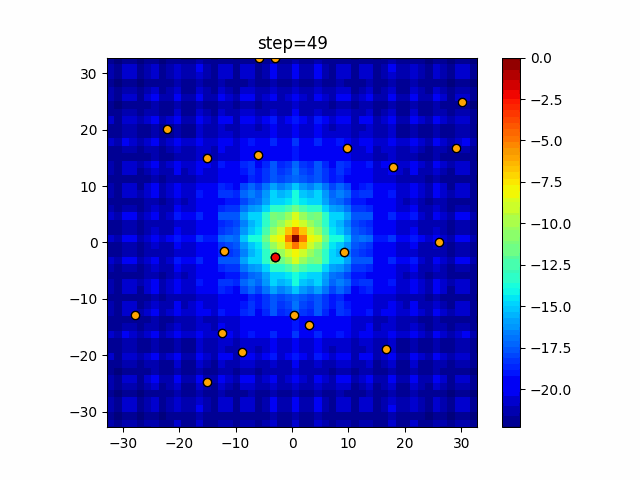
function_Rastrigin
- 1D
- 2D
function_Schwefel
- 1D
- 2D
function_StyblinskiTang
- 1D
- 2D
function_XinSheYang
- 1D
- 2D
Afterword
Replacing the individual with the lowest evaluation value is a feature not found in other algorithms. The reason why learning seems slow in the image is that only one individual is evaluated in one step. (Cuckoo search is similar, 1 step ≒ 1 individual evaluation)
Recommended Posts